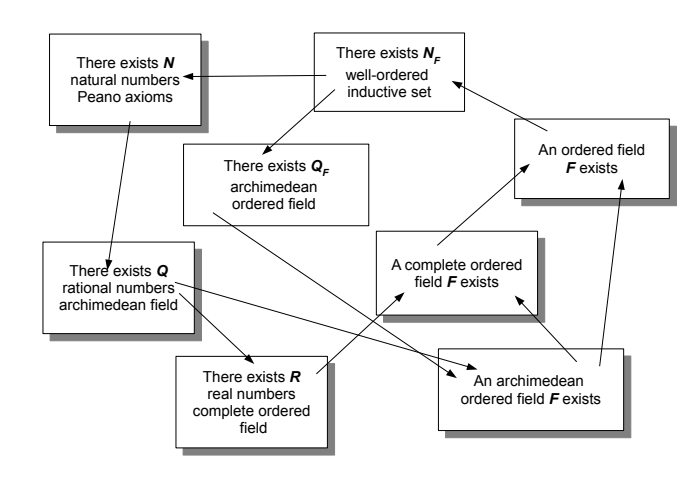
Abstact The Great Theorem : A field which is totally ordered and Dedekind complete exists. And such field is unique up to (unique order-preserving) isomorphism.

그림 출처

In this post, we show that there exsits a field $Q$ which is Archimedian ordered. And we show that if there exists an archimedian oreded field then there exists a totally ordered, Archimedian and complete field $R$ which contains a subfield isomorphic to $Q$. So, the first part of the Great theorem holds. One can show that such field is unique up to isomorphism. Moreover, beteween two complte ordered fields there exists unique isomorphism beteween them.

$\mathbb{R}$ - 실수

실수는 수학에서 굉장히 중요한 개념 중 하나입니다. 우리가 일상에서 사용하는 대부분의 숫자들, 예를 들어 소수점을 가진 수, 양수, 음수, 0 등 모든 것이 실수의 범주에 속합니다. 실수는 보통 $\mathbb{R}$로 표현됩니다.

특성이란?
특성이란 어떤 대상의 고유한 성질이나 특징을 말합니다. 사람에게서는 외모, 취향, 성격, 등의 특징이 있으며, 수학적 대상에서는 그 대상의 특정 성질이나 규칙이 될 수 있습니다.

예를 들어, 실수를 외모, 취향, 성격으로 소개하자면, "totally ordered", "Archimedian", "complete"이라고 말할 수 있습니다. 만약 다른 수 체계가 이러한 세 가지 특성을 모두 갖는다면, 그 수 체계는 실수와 동질적(isomorphic)으로 볼 수 있습니다.

저는 양말을 자주 짝을 안 맞추고 신고다니고, 귤을 좋아하고, MBTI는 INTP입니다

이를 사람에 대한 비유로 들자면, 이러한 특성 (짝짝이 양말 착용, 귤 좋아함, MBTI는 INTP)을 갖는 다른 사람을 만나도 그 사람은 저와 동질적이라고 볼 수 있습니다.

하지만 중요한 것은 동질적(isomorphic)이라는 수학용어가 시사하는 바는, 그들은 대강 비슷한 사람이라는 것이 아니라 그들이 서로가 서로에 대해서 복제된 존재인 것을 나타내고 있다는 것입니다.

이런 겁니다. 예를들어서, 어떤 미친 과학자가 여러분의 DNA를 가지고 있다고 합시다. 그리고 그것을 복제해서 여러 동일한 환경의 연구소에서 여러분의 복제인간들을 만들었습니다.

isomorphism이 주는 느낌은 이렇습니다. DNA도 같고 환경도 같으니, 그 복제인간들은 똑같은 행동을 하겠지.

위 예시에서 조금 주의해야 하는 게, (복제인간 예시와 달리) 수학에서 진짜 실수이란 것은 없습니다. 그러니깐, 그니깐 original real number 이런 것은 없어요. 그러니깐, 어떤 체(field)가 이 세 가지 특성 "totally ordered", "Archimedian", "complete"을 모두 갖추고 있다면, 그 체(field)는 정의에 의해서 실수입니다.

뭐라는 거 대체?

별 내용 아닙니다. 저는 지금까지 다양한 방식으로 실수를 구성하더라도 그 결과는 항상 우리에게 익숙한 실수 체계와 동일하다는 말을 하고 있습니다. (그리고 그 우리에게 익숙한 실수체계가 원본실수여야하는 당위성이 없기 때문에, 구성적 방식이 아닌, 특성을 이용한 방식으로 실수를 정의합니다.)

• 전순서 Totally ordered : 임의의 두 원소$x,y$를 비교하여 하나가 다른 것보다 '작다', '같다', '크다'를 판단하여 $x<y$ 또는 $x=y$ 또는 $x>y$라 결론 낼 수 있는 성질을 말합니다. 예를들어서, 복소수는 Totally ordered가 아닙니다. $i$랑 1의 크기가 같지만 $i=1$이라 말 할 수 없으니깐요.

• 완비성 (Complete): 체 안에 '빈틈'이 없는 성질을 말합니다. 예를 들면, 유리수에는 빈틈이 있습니다. $\sqrt{2}$ 같은 숫자는 유리수가 아니지만, 유리수로 이루어진 숫자열들의 극한으로 $\sqrt{2}=1.4142135623 7309504880 1688724209 6980785696 71875376945...$로 표현할 수 있습니다. 실수나 복소수는 이런 '빈틈'이 없기 때문에 완비성을 가집니다.

• 절대값:절대값은 쉽게 말해 크기입니다. 그런데, 순서기호 $<$의 개념과 조금 다릅니다. 예를들어서, 복소수 $i$의 절대값은 무엇일까요? 복소평면에서의 $i$가 원점과 거리가 1이므로 1이라 할 수 있을 것입니다. (물론 다르게 정의하는 것도 가능합니다. 단 아래 4조건을 만족해야합니다.) 절대값에는 정확히 두 종류가 있습니다. 아르키메데스 성질을 만족하는 것을 'Archimedean', 만족하지 않는 것을 'non-Archimedean'이라고 합니다

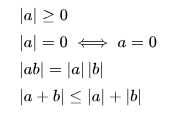
• 아르키메데스 성질 (Archimedean): 이 성질은 얼마나 작은 양의 숫자가 주어지든, 그 숫자를 충분히 많이 더하면 어떤 주어진 숫자보다도 절대값이 큰 수를 얻을 수 있다는 것을 의미합니다. 예를 들어, 실수에서 0이 아닌 모든 숫자에 대해, 그 숫자를 계속 더하면 어떤 숫자보다도 크기가 커질 수 있습니다. 예를들어서 $-1$을 계속 더해서, $10$보다 절대값이 크게 하는 것을 생각해봅시다. 그러면, $-1$을 11번 더하면 $-11$로서 (순서적 비교에서 $-11<10$이지만) 절대값으로 비교하면 $-11$의 절대값이 10의 절대값 보다 더 큽니다. 예를들어서, 실수와 복소수는 아르키메데스 성질을 만족합니다.

$\mathbb{C}$는 복소수들의 집합 그리고 $\mathbb{R}$은 실수들의 집합을 뜻합니다. 그들은 모두 complete합니다. 근데, 사실 complete field 자체가 매우 특수한 수학 대상입니다.

절대값이 주어진 complete field부터가 엄청나게 강력한 조건입니다. 만약 여기에, archimedian을 추가하면, $\mathbb{C}$ 또는 $\mathbb{R}$만 남게 되고(Ostrowski's theorem), 여기에 totally ordered 조건을 추가하면, $\mathbb{R}$만 남습니다.

그리고 totally ordered complete field는 (정의상, 이것은 Least upper bound 성질을 만족하는 totally ordered field인데) 여기에는 archimedian 절대값을 줄 수 밖에 없습니다.

archimedian이란 용어는 실수를 정의하지는 않습니다. 그러나 archimedian은 매우 중요한 실수의 성질 입니다. 이것은 고전 기하학의 평행선 공리와 같은 겁니다. 그럼 archimedian은 무엇이며, 이것을 거절하면 어떻게 될까요? 그러면, 지금껏 모르던 새로운 수체계가 나타납니다. 여기서 꼭 확인해보시기 바랍니다.

실수의 기본 연산:

사칙연산

사실 덧셈과 곱셈이 전부입니다. '사칙연산'은 용어의 혼용이죠. 이칙연산이라 해야 말이 맞습니다...

1. 덧셈 $+$ : 두 수 $a$와 $b$를 합칠 때 사용하는 연산입니다.

   • 표기: $a + b$

2. 곱셈 $\cdot$ : 두 수 $a$와 $b$를 곱할 때 사용하는 연산입니다.

   • 표기: $a \cdot b$

3. 덧셈의 역원과 뺄셈 $-$ : 실수 $a$에 대해서, $a+x=0$을 만족시키는 실수 $x$가 유일하게 존재하며, 그 수를 $-a$라고 표기합니다. $a+(-b)$를 간단히 $a-b$라고 적고, 이 연산을 뺄셈이라고 부릅니다.

4. 곱셈의 역원과 나눗셈 $/,\frac{\cdot}{\cdot}$ : $0$이 아닌 실수 $a$에 대해서, $a\cdot x = 1$을 만족시키는 실수 $x$가 유일하게 존재하며, 그 수를 $1/a$ 또는 $\frac{1}{a}$라고 표기 합니다. $a\cdot \frac{1}{b}$를 간단히 $a/b$ 또는 $\frac{a}{b}$라고 적고 이 연산을 나눗셈이라 부릅니다.

체

실수는 체(field)입니다.

체 (Field)는 대수학에서 중요한 기본 개념 중 하나입니다. 체는 덧셈, 곱셈 연산이 가능한 다음 기본 성질이 만족하는 집합으로서 정의됩니다.

체의 기본 성질들:

1. 덧셈과 곱셈에 대한 닫힘 (Closed): 체의 임의의 두 원소를 더하거나 곱하면, 그 결과도 체의 원소여야 합니다.
2. 교환 법칙 (Commutative law): 덧셈과 곱셈 모두 교환 법칙을 만족합니다. $a + b = b + a$, $ab = ba$.
3. 결합 법칙 (Associative law): 덧셈과 곱셈 모두 결합 법칙을 만족합니다. $a + (b + c) = (a + b) + c$, $a(bc) = (ab)c$.
4. 항등원 (Identity elements): 0은 덧셈의 항등원, 1은 곱셈의 항등원입니다. $a + 0 = a$, $a \times 1 = a$.
5. 역원 (Inverses): 체의 모든 원소는 덧셈과 곱셈에 대한 역원을 가집니다. 임의의 원소 $a$에 대해, $-a$는 $a$의 덧셈에 대한 역원, $a^{-1}$는 $a$의 곱셈에 대한 역원(단, $a \neq 0$)입니다.
6. 분배 법칙 (Distributive law): 곱셈이 덧셈에 대해 분배됩니다. $a(b + c) = ab + ac$.

예시:

• 실수, 유리수, 복소수는 모두 체의 예시입니다.
• 정수 집합은 곱셈에 대한 역원이 없기 때문에 체는 아닙니다.

순서

실수에는 "순서"라는 개념이 존재합니다. 순서는 실수들 사이의 관계를 나타내며, 이 관계를 부등호($<$)를 통해 표현합니다. 이런 순서 관계는 우리가 수를 이해하고 비교할 때 굉장히 중요합니다. 아니 그 반대인 것 같습니다. 순서가 명확하게 존재하기 때문에, 실수를 더 이해하기가 더 쉬워집니다.

1. 부등호 $(<)$

부등호는 두 수 사이의 상대적 크기나 위치를 비교하는 데 사용됩니다. 예를 들어, $3 < 5$는 3이 5보다 작다는 것을 의미합니다.

2. Trichotomy (삼분법칙)

어떤 두 실수 $a$와 $b$에 대해 오직 하나의 다음 중 하나만이 참입니다:

• $a < b$
• $a = b$
• $a > b$

즉, 두 실수는 서로 같거나, 하나는 다른 하나보다 크거나 작습니다.

3. Transitivity (전이성)

만약 $a < b$ 그리고 $b < c$ 라면, $a < c$ 입니다.
이는 숫자의 순서가 "연속적"이라는 것을 의미합니다.

4. Compatibility with Addition (덧셈과의 호환성)

만약 $a < b$ 라면, 어떤 수 $c$에 대해 $a + c < b + c$ 입니다.
이는 숫자를 더하면 순서가 변하지 않는다는 것을 의미합니다.

5. Compatibility with Multiplication (곱셈과의 호환성)

만약 $a < b$ 그리고 $c > 0$ 이라면, $ac < bc$ 입니다.
하지만 $c < 0$ 이면, 부등호의 방향이 바뀝니다: $ac > bc$.
곱셈은 덧셈과는 달리, 곱하는 수에 따라 순서가 바뀔 수 있습니다.

실수의 정의:

실수가 무엇인지 명확하게 말하는 것은 꽤 복잡합니다. 실수를 명확하게 말하기 위해서는 먼저 유리수를 명확하게 이야기하고, 그 이후, 유리수를 이용해서 실수를 명확하게 이야기합니다. 먼저 실수를 구성하고 있는 것들이 무엇인지 간략히 소개하겠습니다.

기본 연산 성질 (포스트에 적은 것 + field axiom) 그리고 순서 성질 그리고, 여기에 더해서, Least Upper Bound Property은 실수를 구성하는 필요충분적인 성질입니다. 즉, 이 성질들을 모두 만족하는 순서체들은 모두 똑같으며 (up to unique order preserving field isomorphism) 이것을 실수라고 부릅니다.

• 자연수: 1, 2, 3, 4, ... 와 같이 0을 제외한 양의 정수입니다.

• 정수: ... , -3, -2, -1, 0, 1, 2, 3, ... 과 같이 음의 정수와 0, 그리고 양의 정수를 포함한 수들입니다.

• 유리수: 분자와 분모로 이루어진 수로, 분모가 0이 아닌 정수의 비율로 표현되는 수입니다. 예를 들어, $\frac{3}{4}, \frac{7}{2}, \frac{-5}{1}$ 등이 있습니다.

• 무리수: 유리수로 표현할 수 없는 수입니다. 대표적인 예로는 제곱근 $\sqrt{2}$, 원주율 $\pi$ 등이 있습니다.

무리수는 단순히 실수이면서 유리수가 이닌 수입니다. 즉, 위의 표현은 무엇이 무리수인지 (실수가 무엇인지 명확하지 않다면) 전혀 알려주지 않습니다. 유리수가 구성된 경우, 실수를 구성하기 위해서 먼저 고려해야하는 것은 실수의 성질입니다. 그리고 그 다음 실수의 성질을 만족하는 방식으로 실수를 구성합니다.

Completeness

한마디로 말해서, 실수는 유리수를 보강하여 complete하게 만든 결과를 지칭합니다. 여기서는 Least upper bound이 구성한 실수가 complete하다는 것을 보입니다.

실수는 연속적인 성격을 가집니다. 그렇기 때문에 수직선 위에 모든 위치에 대해서, 그 위치에 해당하는 실수가 유일하게 존재 합니다.

수직선 위의 어떤 위치를 고르든지 그 위치를 나타내는 유리수의 수열이 존재합니다. 그 위치가 (유리수인 경우는 당연해서, 넘어가고) 유리수에 해당하는 위치가 아닌 경우, 그 위치를 기준으로 매우 가까이에 있는 유리수를 (그 위치를 포함하는 영역을 아무리 좁게 제시한다고 할지라도) 찾아낼 수 있습니다. 점점 영역을 좁혀가며, 유리수들의 수열을 구성한다면, 그 수열을 구성하는 수들의 (수직선 위에서의) 위치들의 모양이 점점 뭉쳐져갑니다. 따라서, 그 수열의 극한이 반드시 존재하며, 그 극한에 해당하는 수가 곧 그 위치에 대응하는 수가 됩니다. 따라서, 수직선위의 모든 위치에 대해서 그 위치에 해당하는 실수가 적어도 하나 존재합니다. 더 나아가서, 수열의 구체적인 구성과 상관없이 그 극한값은 유일합니다. 왜냐하면, 다른 수열을 생각하더라도, 그 수열과 다른 수열의 차이가 0에 수렴하니깐요. 따라서 수직선은 실수입니다.

위의 글에서 문제가 되는 부분이 있습니다. 그것은 수직선 위의 점들의 수열이 점점 뭉쳐진다는 표현입니다.더 나아가서, 수열이 점점 뭉쳐진다는 게 무엇을 뜻하는 것인지 명확하다고 볼지라도 그게 곧 그 수열의 극한의 존재를 증명하지는 않습니다.

극한의 정의는 극한 값$L$이 먼저 제시가 되어있는 형태이므로, 그 위치에 해당하는 수의 존재가 명확하지 않다면, 위의 논리를 극한의 정의를 이용해서, 정당화하는 것이 불가능합니다. 그래서, 우리는 코시 수열을 생각합니다. 수열의 위치들의 모양이 점점 뭉쳐져가는 모양새이면, 그 수열을 코시 수열이라 부릅니다.

이것을 더 명확하게 말하기 위해서는, 두 유리수 $x,y$에 대해서 그 거리를 절대값 $| x -y|$으로 정의하고, 실수들로 구성된 모든 코시수열이 수렴함을 보여야 합니다.

코시 수열의 정의
코시 수열은 수열의 모든 항들이 "충분히 큰" 인덱스를 갖는 경우, 그 임의의 두 항 사이의 거리가 아주 작아지는 성질을 갖는 수열입니다. 보다 구체적으로 다음의 정의를 따릅니다.

---

한 수열 $\{ a_n \}$가 모든 양의 실수 $\epsilon > 0$에 대해 다음의 성질을 만족하면 코시 수열이라고 합니다:

존재하는 어떤 자연수 $N$ (즉, $N$은 $\epsilon$에 의존적)이 있어서, 모든 $n, m > N$에 대해:

$|a_n - a_m| < \epsilon$

---

실수와 코시 수열:

실수의 전체 집합 $\mathbb{R}$에서의 중요한 성질 중 하나는, 코시 수열이 항상 수렴한다는 것입니다. 다시 말하면, 만약 어떤 수열이 코시 수열이라면, 그 수열은 실수의 어떤 값에 수렴합니다.

이러한 성질을 완비성(Completeness) 라고 합니다. 완비성은 실수의 기본적인 특성 중 하나이며, 이것은 실수가 유리수와 다른 점 중 하나입니다. 유리수의 집합에서는 코시 수열이 있음에도 불구하고 수렴하지 않는 경우가 있는데, 예를 들어 무리수 $\sqrt{2}$의 연속 근사값으로 이루어진 수열이 그러한 예입니다.

이렇게 완비성은 실수 체계의 중요한 특성을 나타내며, 그것은 수학적 분석 및 다양한 응용에서 중요한 역할을 합니다.

Least Upper Bound Property

실수가 완비성(Completeness)을 갖추도록 실수를 구성하는 방법 중 하나입니다.

Least Upper Bound Property (LUBP)을 이해하기 위해서는 먼저 상한(upper bound)과 최소 상한(least upper bound)에 대한 개념을 알아야 합니다.

상한 (Upper Bound):

집합 $S$가 주어졌을 때, 만약 어떤 수 $b$가 모든 $S$의 원소보다 크거나 같으면 (또는 $S$의 모든 원소가 $b$보다 작거나 같으면), $b$를 집합 $S$의 상한이라고 합니다.

최소 상한 (Least Upper Bound):

집합 $S$의 모든 상한 중에서 가장 작은 값을 집합 $S$의 최소 상한이라고 합니다. 이것을 종종 supremum이라고도 부르며, "sup S" 또는 "sup($S$)"로 표기합니다.

Least Upper Bound Property (LUBP):

만약 어떤 집합 $S$가 실수 중 적어도 하나의 상한을 가지면, 그러한 집합은 반드시 최소 상한을 갖는다는 성질입니다.

예제:
집합 $S = \{ x \in \mathbb{R} : x^2 < 2 \}$를 생각해보겠습니다. 이 집합의 원소는 모두 $\sqrt{2}$보다 작습니다. 따라서 $\sqrt{2}$는 이 집합의 상한 중 하나입니다. 하지만 이것이 최소 상한인지는 바로 알 수 없습니다. 사실, $\sqrt{2}$는 이 집합의 최소 상한입니다.

왜 LUBP가 중요한가?

뭐가 진짜 실수야? 사실 진짜 실수란 것은 없습니다. LUBP를 만족 한다면, 그게 곧 실수에요.

1. 다양한 실수 표현의 존재: 우리가 일상에서 사용하는 실수 표현(소수점 표기법, 수직선)외에도, 수학적으로 실수를 표현하는 다양한 방법이 존재합니다. 예로, 데데킨드의 절단이 있습니다.

2. 이 다양한 표현들의 공통점: 이러한 다양한 표현법들은 서로 다르게 보일 수 있지만, LUBP를 만족하고, 동일한 연산 법칙과 순서 법칙을 갖습니다.

3. 실수의 유일성: 그 공통점은 사실, 실수를 정의하는 필요충분적인 성질입니다. 다시말해서, 이 성질들(연산법칙 + 순서법칙 + LUBP)을 모두 만족하는 수체계는 $\mathbb{R}$이 유일합니다. 증명은 여기서 즉, 이 $\mathbb{R}$의 다양한 표현법들은 단순히 '표기'만 바뀐 것일 뿐, 그 연산 및 순서를 기준으로 관찰하면 완전히 같다는 겁니다. (같은 것은 같은 것이다- 이인석 교수)

핵심

LUBP는 거리 대신 순서를 이용해서 기술한 완비성의 정의입니다. 즉, 순서가 주어진 (totally ordered) 그러나 거리가 주어지지 않은 경우, LUBP를 선언하면 거리가 주어지지 않은 상태에서도 완비하다라고 말할 수 있다는 장점이 있습니다. 왜냐하면, LUBP로 구성한 실수에 절대값 거리를 부여한 경우 거리를 기반으로 정의한 (즉, 코시수열로 정의한) 완비성 또한 만족하게 되기 때문입니다.

1. LUBP로 확인하는 실수의 유일성
   수학적으로, 실수의 연산구조, 순서구조, 그리고 LUBP를 만족하는 모든 체계는 서로 구별되지 않습니다.

2. LUBP로 구성한 실수의 완비성

   실수의 완비성 보이기는 코시수열의 정의와 LUBP를 알고 있는 사람에게 매우 좋은 연습문제입니다.

   완비성의 개념은 실수 체계의 기본 구조와 근본적인 성질을 나타냅니다. LUBP는 완비성의 한 형태로, 실수 체계가 어떤 집합에 대해서도 그 집합의 최소 상한을 포함한다는 것을 보장합니다. 이것은 실수 체계가 "구멍이 없다는" 것을 의미하며, 이는 해석학에서 굉장히 중요한 성질입니다.