이차형식의 표준형식

이차형식의 표준화란, 특별한 기저를 찾아서 이차형식의 행렬 표현이 대각행렬이 되도록 하는 것을 의미합니다.

다음 정리를 증명하고자 합니다.

모든 이차형식 $\psi(\bold x)$에 대해서, 다음과 같이 표현을 가능하게 하게 하는 기저가 존재합니다.
$\psi(\bold x)=\lambda_1 x_1^2 + \lambda_2 x_2^2 + \cdots + \lambda_n x_n^2$, 여기서 $x_i$는 $\bold x$의 좌표입니다.

다시 말해서, 선택한 기저가 $\beta$라면 $[\bold x]_\beta = \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix}$입니다. 그리고 $x_i$에 대해서, 위의 식이 성립합니다.
자세히 말해서, $\psi(\bold x)$를 나타내는 대칭쌍선형 형식을 $\varphi$라 합시다. 이것은 $\psi(\bold x)= \varphi(\bold x, \bold x)$가 성립하게 하는 유일한 쌍선형형식 $\varphi$입니다. 그러면, 선택한 기저를 $\bold b_1,\bold b_2,\ldots, \bold b_n$이라 할때, 다음이 성립합니다.

• $\varphi(\bold b_i, \bold b_j)=0$ 만약, $i \ne j$이면
• $\varphi(\bold b_i, \bold b_i)=\lambda_i$

직교대각화와 다른점 찾고 가기.

이것은, 직교대각화랑 다른 개념입니다. 그리고, 위의 수식의 $\lambda$들은 고유값이 아닙니다.

1. $\lambda_i$는 유일하지 않습니다. (오히려 그 반대로, 무수히 많습니다.) 왜냐하면, $\bold b_1,\bold b_2,\ldots,\bold b_n$ 대신에, $\gamma =\{\bold c_i = P \bold b_i\}$을 선택하면 , 쌍선형형식의 기저변환 공식$\Phi_\gamma = P\Phi_\beta P^\top$에 의해서 (만약, 어떤 이유로 $i$와 $j$가 다를 때마다, $\varphi(\bold c_i, \bold c_j)=0$임을 알고 있다면, 단순히 $\varphi(\bold c_i, \bold c_i)$를 계산해도 되죠 ) 계수 $\lambda_i$가 바뀝니다. 만약, $P=kI$ (단, $k \ne 0$)이면, $x_i^2$의 계수가 $k^2\lambda_i$로 바뀝니다.

2. 이차형식의 행렬 표현들끼리는 서로 닮지 않았습니다. (선형변환의 행렬표현은 서로 닮았습니다.)

---

증명을 위해 필요한 내용들을 먼저 소개 합니다.

부분공간과 행렬 표현

우리가 잘 아는, Rank Nullity 정리를 행렬 표현으로 다시 해석해 봅시다.

몇몇 정의들

$\oplus$기호를 소개합니다.

벡터공간 $V$에 대해서,$V$의 부분 집합 $W \subset V$가 벡터공간이면 $W$를 $V$의 부분공간이라 부릅니다. 예를들어서 $V$의 0벡터만 모은 집합 $(\bold 0)$ 그리고 $V$는 $V$의 부분공간의 당연한 예시입니다. 그리고 $\bold v \in V$에 대해서, 다음과 같이 정의된 집합 $\{k\bold v:k\in K\}$ 역시 자명한 부분공간이며, $\text{span}\{\bold v\}$ 또는 간단히 $(\bold v)$라 표기합니다.

두 부분공간 $V_1,V_2 \subset V$에 대해서 다음을 벡터공간의 합이라 부릅니다.
$V_1 + V_2 :=\{\bold x_1+\bold x_2 \in V : \bold x_1 \in V_1, \bold x_2 \in V_2\}$
집합 $V_1 + V_2$이 부분공간이기 때문에, 위의 정의는 자연스럽게 확장하여
다음을 정의할 수 있습니다. $V_1 + V_2+\ldots + V_k$

부분공간 $V_1,V_2,\ldots,V_k \subset V$에 대해서, 직접합 $\oplus$는 다음과 같이 정의됩니다.
각각의 $\bold x \in V_1+\ldots + V_k$에 대해서, 유일한 $(x_1,\ldots,x_k)\in K^k$가 존재해서
$\bold x = x_1 \bold x_1 + x_2 \bold x_2 + \ldots + x_k \bold x_k$, 여기서 $\bold x_i \in V_i$가 성립하면, $V=V_1\oplus V_2 \oplus \ldots \oplus V_k$라 적고, $V$를 $V_1,\ldots,V_k$의 직접합(direct sum)이라 부릅니다.

몇몇 정리들

$\oplus$ 기호에 익숙해질 수 있도록, 몇몇 당연한 내용들을 소개합니다.

$V=V_1\oplus V_2 \oplus \ldots \oplus V_k, \iff \left[ \bold x_1 + \bold x_2 + \ldots \bold x_k= 0 \implies \forall i \in\{1,2,\ldots,k\} \ \bold x_i = \bold 0 \right]$
단, $\forall i \in\{1,2,\ldots,k\}, \ \bold x_i \in V_i$

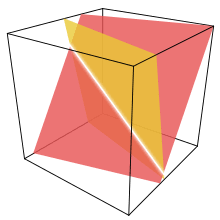
아래 그림은 직합표현이 안 되는 예시입니다. 예를들어서 빨간 공간을 $\textcolor{red}{X}$ 그리고 노란 공간을 $\textcolor{orange}{Y}$라 합시다. 그러면, 두 평면에 교선위 한 점에 대응하는 (원점이 아닌) 벡터 $v$에 대해서, $v$는 $\textcolor{red}{X}$ 과 $\textcolor{orange}{Y}$모두에 속합니다. 다시 말해서, $\textcolor{red}{v}+ \textcolor{orange}{(-v)}=0$은, $\left[ \bold x + \bold x_2= 0 \implies \forall i \in\{1,2\}, \bold x_i = \bold 0 \right]$의 반례가 됩니다.

$\bold x_1,\bold x_2, \ldots ,\bold x_k$ 는 선형독립입니다. $\iff \text{span}\{\bold x_1,\bold x_2, \ldots ,\bold x_k\}=(\bold x_1) \oplus (\bold x_2) \oplus \ldots \oplus (\bold x_k)$
단, $\forall i \in\{1,2,\ldots,k\}, \ \bold x_i \in V$

$\bold x_1,\bold x_2, \ldots ,\bold x_n$은 $V$의 기저입니다. $\iff V = (\bold x_1) \oplus (\bold x_2) \oplus \ldots \oplus (\bold x_n)$
단, $\forall i \in\{1,2,\ldots,k\}, \ \bold x_i \in V$

만약 벡터공간 $V_1,V_2$가 유한차원 벡터공간 $V$의 부분공간이고 $W=V_1 \oplus V_2$이면, $W$의 차원은 $V_1$과 $V_2$의 차원의 합과 같습니다.

만약 $V=V_1+\cdots + V_r$이고, $V$의 차원이 $V_i$의 차원들의 합과 같으면($i=1,2,\ldots,r$), 다음이 성립합니다.$V=V_1\oplus V_2 \oplus \ldots \oplus V_r$

Rank Nullity Theorem

$V$의 차원을 $n$ 그리고 $T:V\to W$의 rank를 (다시 말해서, $T$의 image의 차원을) $r$이라 하면 다음이 성립합니다.

1.RANK NULLITY 정리 $\text{Ker} \ T$의 차원은 $n-r$이다.
2.그리고, $T$의 행렬 표현 $[T]_\beta^\gamma$가 다음과 같은 블록대각행렬이 되도록, $V$와 $W$의 기저 $\beta$, $\gamma$를 선택할 수 있다.
$\begin{bmatrix}I_r & 0 \\ 0 & 0\end{bmatrix} =\begin{bmatrix} 1 &\cdots &0 & 0 & \cdots &0\\ \vdots& \ddots& \vdots & \vdots & \ddots & \vdots \\ 0&\cdots & 1 & 0 & \cdots & 0 \\ 0&\cdots & 0 & 0& \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots&\ddots &\vdots\\ 0& \cdots & 0 & 0 & \cdots & 0\end{bmatrix}$
여기서, $I_r$은 $r\times r$ 단위행렬이다.

증명

먼저, Rank Nullity 정리를 증명합니다.

독자는 선형사상 $T$를 이용하여, $\text{Ker} T$가 벡터공간임을 증명할 수 있습니다. 그리고 독자는 공역을 제한해서 얻은 $T|^{\text{Im}T} : V \to \text{Im}T$ (여기서, $T|^{\text{Im}T}$는 $T|^{\text{Im}T}(v) = T(v)$으로 정의된다.)가 surjective(Onto)한 선형사상임을 증명한 뒤 이를 이용해서, $T$의 image $\text{Im}T$가 벡터공간임을 증명할 수 있습니다.

주의: 단순히 공역을 제한한다고 그 제한된 집합이 벡터공간이 되는 것이 아니다.
사실 Rank Nullity정리는 대수학에서 다루는 Isomorphisim 정리의 특수한 경우로, (독자가 대수학을 아는 경우) 그 정리에서 Image가 Domain을 Kernel로 Quotient한 것이 동형이던 것을 기억합시다.

그리고 (기저의 존재성을 이용하여 ) 독자는 다음을 보일 수 있습니다.

1. 다음을 만족하는 $V$의 부분공간 $V_r$이 존재한다.
   $V=V_r \oplus \text{Ker} \ T$

2. 다음을 만족하는 $W$의 부분공간 $W_{n-r}$이 존재한다.
   $W=\text{im} T \oplus W_{n-r}$

직합$\oplus$의 성질에 의하여 좌변 차원은 우변 차원 합과 일치해야합니다.
따라서, $V_r$의 차원은 $n-\text{dim}(\text{Ker} T )$
그리고 $W_{n-r}$의 차원은 $n-r$임을 바로 알 수 있습니다. (물론, 정리의 첫번째 결론에 의해서, $V_r$의 차원은 $r$입니다. 그러나, 아직 이것은 논리적으로 도출되지 않았습니다.)

이제, 우리는 $T$의 정의역을 $V_r$로 제한해서 선형변환 $T|_{V_r}:V_r \to V$을 생각할 것입니다.

$V_r$이 벡터공간이므로, $T|_{V_r}:V_r \to V$ (여기서, $T|_{V_r}:V_r \to V$는 $T|_{V_r}(v) = T(v)$로 정의된다)은 선형변환입니다.

그러면 $T|_{V_r}$의 kernel은 $(\bold 0)$입니다. 왜냐하면, 정의에 의해서 $Ker \ T|_{V_r} \subseteq V_r$ 그리고 $Ker \ T|_{V_r} \subseteq Ker \ T$이고, $V=V_r \oplus \text{Ker} \ T$라는 조건에 의해서, $T \cap \text{Ker} T = (\bold 0 )$이기 때문에, $Ker \ T|_{V_r} \subseteq (\bold 0 )$이기 때문입니다. 그리고 $T|_{V_r}$의 image는 $T$와 같습니다. (그 이유의 설명은 독자에게 맡깁니다.) 따라서, 다음 정리에 의해서, $V_r$과 $\text{im} \ T$의 차원은 $r$로 같습니다.

정리 선형변환 $T:V\to W$가 일대일이면, $V$와 $T|_V$의 차원이 같습니다.
증명 $V$의 기저 $\bold b_1,\ldots, \bold b_r$에 대해서, $T(\bold b_1), T(\bold b_2), \ldots, T(\bold b_r)$이 선형독립이고, 이것으로 구성한 집합이 자명하게 $\text{im} \ T$의 spanning set이므로 $T|_V$기저입니다. 한편, $T$가 일대일이므로, $T|_V$의 기저는 $V$의 기저와 크기가 같습니다.

$T$의 행렬표현에 대한 주장을 증명합니다.

독자는, (벡터공간 차원의 유일성을 이용하여, 더 근본적으로는 Steinitz exchange lemma를 이용하여) 다음을 보일 수 있습니다.

1. $V= V_r \oplus \text{Ker} \ T$의 기저, $\bold v_1, \bold v_2,\ldots,\bold v_n$이 다음을 만족하도록 선택할 수 있다. $\bold v_1,\ldots,\bold v_r$은 $V_r$의 기저이고 $\bold v_{r+1} \ldots, \bold v_n$은 $\text{Ker} \ T$의 기저이다. 다시말해서, $T(\bold v_{r+1}) = \cdots = T(\bold v_n) =0$이다.
2. $\bold w_i = T(\bold v_i)$, $i=1,\ldots, r$이라 하면, $\bold w_1, \bold w_2, \ldots, \bold w_r$은 $\text{im} \ T$의 기저이다.
3. $W$의 차원을 $m$이라 하자. ( $W \supset \text{im} T$이므로 $m\ge r$이다.) 그러면, $\bold w_{r+1},\bold w_{r+2}, \ldots, \bold w_m$이 존재해서 다음을 만족한다.
   • $\bold w_1, \bold w_2, \ldots, \bold w_r$은 $\text{im} \ T$의 기저이다. (왜냐하면, $\bold w_i= T(\bold v_i)$, for $i\le r$)
   • $\bold w_{r+1},\bold w_{r+2}, \ldots, \bold w_m$
   • $\bold w_1,\ldots,\bold w_m$은 $W$의 기저이다.

위에 적은 성질이 만족하도록 잘 골라서 구성한, $V$의 기저 $\beta$를 $\bold v_1,\ldots, \bold v_n$이라 하고 $W$의 기저 $\gamma$를 $\bold w_1,\ldots, \bold w_m$ 그러면

$T(\bold v_1) = 1\bold w_1 + 0 \bold w_2 + \ldots + 0 \bold w_r + 0 \bold w_{r+1} + \ldots + 0 \bold v_m$
$T(\bold v_2) = 0\bold w_1 + 1 \bold w_2 + \ldots + 0 \bold w_r + 0 \bold w_{r+1} + \ldots + 0 \bold v_m$
$\vdots$
$T(\bold v_r) = 0\bold w_1 + 0 \bold w_2 + \ldots + 1 \bold w_r + 0 \bold w_{r+1} + \ldots + 0 \bold v_m$
그리고, $T(\bold v_{r+1}) = \cdots = T(\bold v_n) =\bold 0$이 성립합니다. 다시 말해서, 행렬표현에 대한 정리의 결론이 성립합니다.