리처드 벨만이 만든 최적화 방법

어떤 문제를 단순화시켜
가장 간단한 방법을 반복해나가면서
순차적으로, 누적하며
최적의 값(정답)을 구하는 방식

모든 방법에 대해 가능성을 탐색해보며
최적의 값을 찾아낸다

예시

파스칼의 삼각형

https://www.acmicpc.net/problem/1932

위 그림은 크기가 5인 파스칼의 삼각형의 한 모습이다

맨 위층 7부터 시작해서
아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때,
이제까지 선택된 수의 합이 최대가 되는 경로를 구하자

아래층에 있는 수는
현재 층에서 선택된 수의
대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

• 풀이
  상단의 두 항 중에서
  큰 값과 현재 값을 더하는 식으로 진행

더해진 결과 값을 이용하여
바로 다음 값을 구하는 방식.
계속 누적해온 결과이기에
매순간마다 처음부터 다시 계산하지 않고
이어서 반복

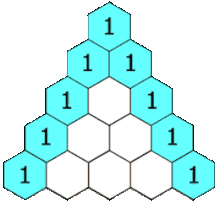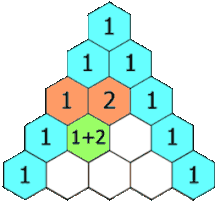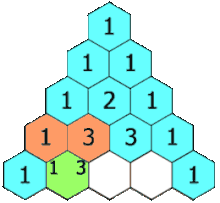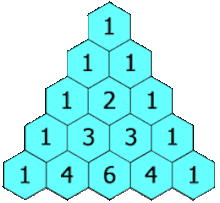
출처 : https://en.wikipedia.org/wiki/Pascal%27s_triangle

n = int(input())
arr = []
for _ in range(n):
	arr.append( list(map(int, input().split())) )

dp = [[0]*i for i in range(1,n+1)]
dp[0] = arr[0]

for i in range(1, n):
    for j in range(i+1):
        if j < len(dp[i-1]): # 오른쪽과 더함
            dp[i][j] = arr[i][j] + dp[i-1][j]
        if j >= 1: # 오른쪽과 더한 것과 왼쪽과 더한 것 중 큰 것으로 결정
            dp[i][j] = max(dp[i][j], arr[i][j] + dp[i-1][j-1])

print(max(dp[-1]))

계단오르기

https://www.acmicpc.net/problem/2579

계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다
각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다

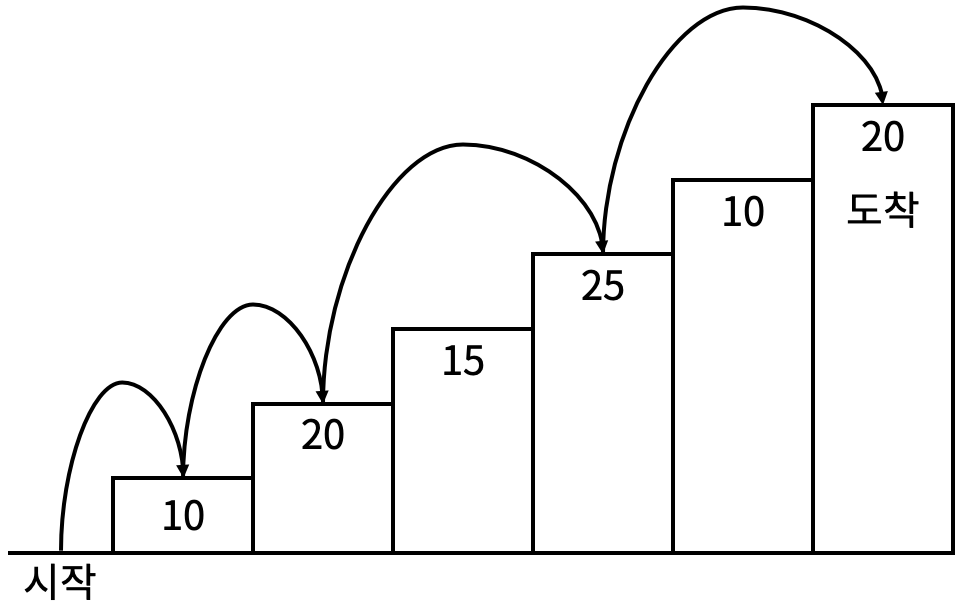
계단 오르는 데는 다음과 같은 규칙이 있다.

계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
마지막 도착 계단은 반드시 밟아야 한다.

n = int(input())
arr = [0]
for _ in range(n):
	arr.append(int(input())
    
dp = [[arr[i], arr[i]] for i in range(n+1)]

for i in range(2, n+1):
    dp[i][0] += dp[i-1][1] # 직전 계단은 건너 뛰어서 온 계단만 가능
    dp[i][1] += max(dp[i-2]) # 두 칸 뒤의 계단은 어디서 오든 상관 없음

print(max(dp[-1]))

# dp의 초기상태
[[0, 0], [10, 10], [30, 20], [15, 15], [25, 25], [10, 10], [20, 20]]

# 1
[[0, 0], [10, 10], [30, 20], "[35, 25]", [25, 25], [10, 10], [20, 20]]

# 2
[[0, 0], [10, 10], [30, 20], [35, 25], "[50, 55]", [10, 10], [20, 20]]

# 3
[[0, 0], [10, 10], [30, 20], [35, 25], [50, 55], "[65, 45]", [20, 20]]

# 4
[[0, 0], [10, 10], [30, 20], [35, 25], [50, 55], [65, 45], "[65, 75]"]