Are you crazy, human?

Are you crazy, human?

Policy와 Value function

Human Being·2022년 8월 11일

0

Reinforcement Learning

목록 보기

4/22

Policy

policy 𝝅하에서 state s에 있을 때 action a를 선택할 확룔

${\pi}(a|s)$ = $P[A_t = a | S_t =s]$

policy는 함수나 열람표(look up table)이다
일반적으로 확률에 따라 action을 선택한다

deterministic policy (결정론적인 정책) : $a = {\pi}(s)$
주어진 state에 하나의 action을 반환
stochastic policy (확률론적인 정책) : ${\pi}(a|s) = P[A_t=a|S_t=s]$
주어진 state에 대해 action들의 확률 분포를 반환
$P^{a}_{ss'}$ 는 확률론적인 정책에서만 존재함

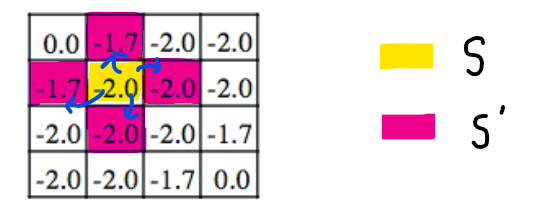
아래 코드는
Gridworld를 기반으로 작성되었다

무작위로 action을 하나 선택하는 경우

    # 특정 상태에서 정책에 따라 무작위로 행동을 반환
    def get_action(self, state):
        policy = self.get_policy(state)
        policy = np.array(policy)
        return np.random.choice(4, 1, p=policy)[0]

열람표에 기반하여 action을 선택하는 경우

    # 상 하 좌 우 동일한 확률로 정책 초기화
 	self.policy_table = [[[0.25, 0.25, 0.25, 0.25]] * env.width
                            for _ in range(env.height)]
                            
    # 마침 상태의 설정
    self.policy_table[2][2] = []
                           
    ~~~                      
                           
    # 상태에 따른 정책 반환
    def get_policy(self, state):
        return self.policy_table[state[0]][state[1]]

optimal policy

모든 state에 대한 가치의 기댓값이 제일 큰 policy

즉 state s에서 그 policy를 따랐을 때의 value가
다른 policy를 따랐을 때의 value보다
높아야 하는 상황이
모든 state에 대해서 적용되어야 한다

state value와 action value

(state-)value function

state s에서 시작한 이후로 policy 𝝅를 따랐을 경우 얻게되는 가치(목표)의 기댓값
미래의 보상값의 총합에 대한 것이므로 value 또한 정확한 값이 아닌 예상값/기대값으로 표현한다

$R_{t+1}$ : 즉각적인 reward

${\gamma}v(S_{t+1})$ : future reward에 discount factor를 곱한 것

G에서 v로 식을 바꾸게 됨으로써
재귀적 표현이 되었고
이 덕분에 동적 계획법의 최적성 원리를 통해
반복을 하면
optimal value function으로 수렴할 수 있게 된다

기댓값

각 사건이 벌어졌을 때의 이득과
그 사건이 벌어질 확률을 곱한 것으로
전체 사건에 대해 합한 값

이산 확률 변수란
확률 변수 X가 아날로그처럼 연속적인 것이 아니라
x1, x2, x3 ... 처럼 셀 수 있을 때의 그 X

이산 확률 변수에 대한 기댓값 공식

$E[X] = ∑_ip_ix_i$

계산 가능한 형태로 변환

기댓값 공식인 $확률 * 이득$ 을 이용한다

E 아래의 𝝅는
policy 𝝅를 따른다는 전제가 깔린 조건부 기댓값 임을 의미한다

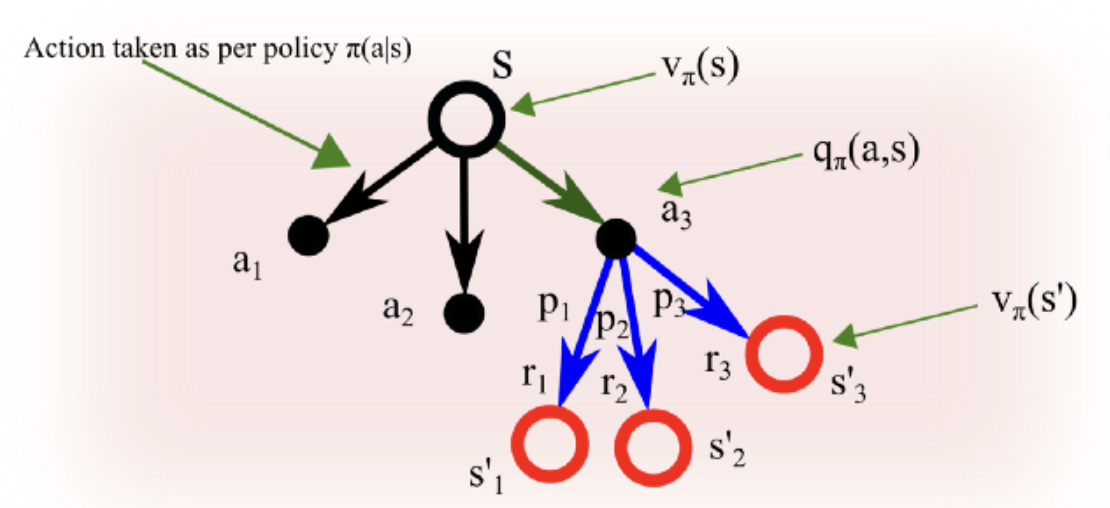
state transition probability는
현재 state s에서 행동 action을 취했을 때,
다음 state s'로 가서 보상 r을 받을 확률를 의미

state s에서 action a를 취하는 확률과,
action a로 인한 결과로 어떤 state로 넘어갈지에 대한 s'에 대한 확률

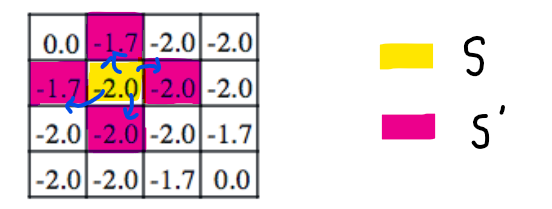
예시

$v(s)$ 를 구하는데 $v(s')$ 가 사용된다는 것은

!! 미래의 값을 가져오는 것이 아니라
다음 state에 누적된 값을 가져온다는 의미 !!
(다음 게시글의 policy iteration을 보면 차이를 느낄 수 있어요)

optimal state-value function

optimal policy가 갖는 state value function

$v_*(s) = max(v_{\pi}(s))$

(state-)action-value function

state s에서 action a를 취하고 그 이후에 policy 𝝅를 따를 경우 얻게되는 value의 기댓값
위의 유도식처럼 정리할 수 있음. 그저 action만 추가된 형태로 된다.

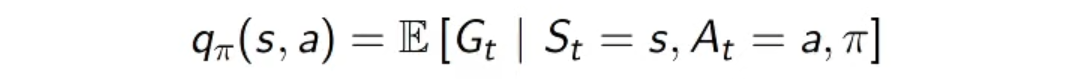
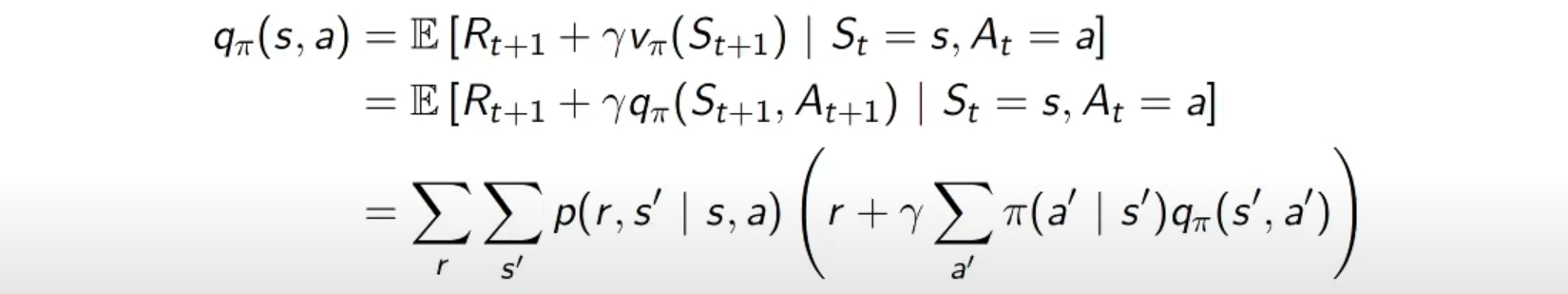
$p(r, s' | s, a)$ 는 $P^a_{ss'}$ 를 의미한다

optimal action-value function

$q_*(s, a) = max(q_{\pi}(s, a))$

이 함수는 state-action 쌍 (s, a)에 대해
state s에서 action a를 선택한 후
optimal policy를 따를 때 얻게 될 가치의 기댓값을 도출한다
$q_*$ 를 $v_*$ 를 이용하여 표현하면 다음과 같이 표현할 수 있다

$q_*(s,a) = E[R_{t+1} + rv_*(S_{t+1})$ | $S_t=s, A_t=a]$

state value와 action value의 관계식

state value function은
action value function을 이용하여 값을 구할 수 있다

policy를 통해 산출된 action에 대한 action value가
바로 그 state의 (state) value가 된다

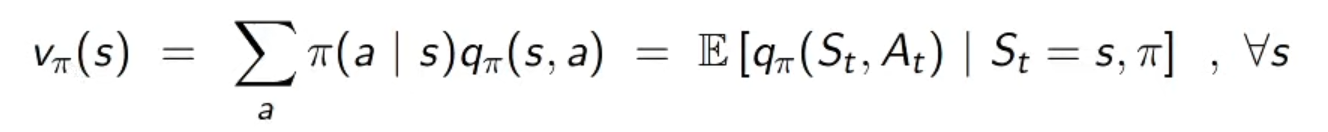
벨만 방정식

벨만 기대 방정식

벨만 최적 방정식

벨만 기대 방정식에 max를 붙인 형태

식을 잘 보면 v=max(q) 로 둘의 상관관계를 나타낼 수 있다

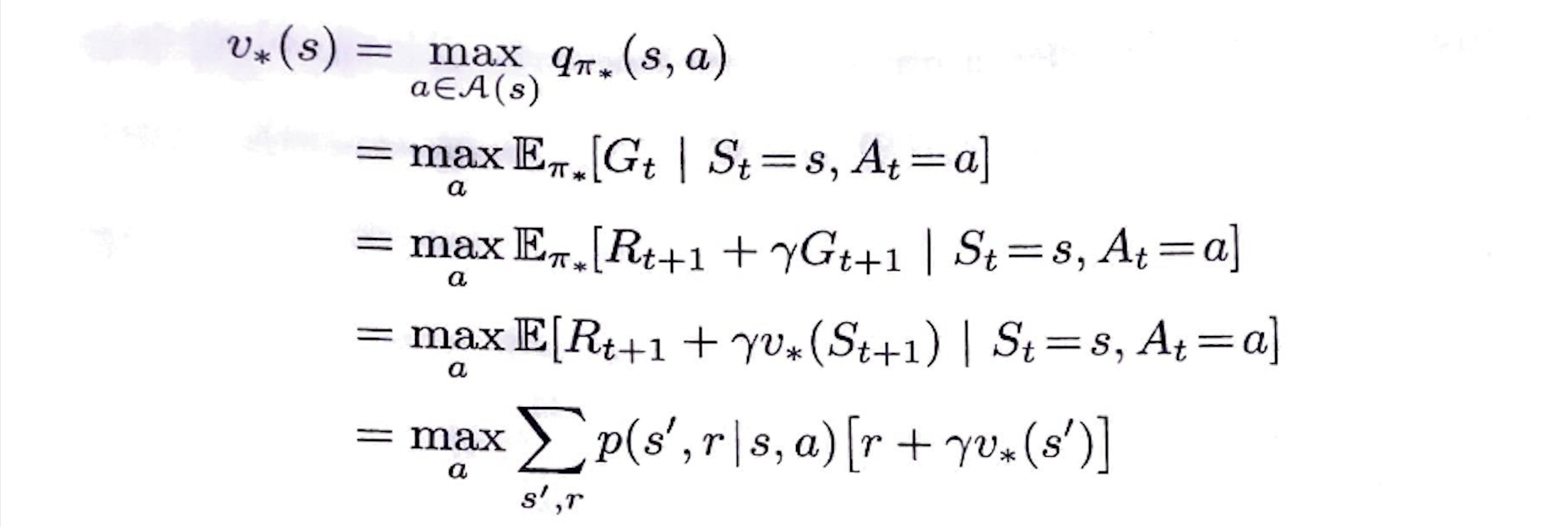
optimal policy를 따르는 state의 value는,
그 state에서 선택할 수 있는
가장 좋은 action을 행했을 때
나오는 reward의 기댓값(Goal)과
같아야 한다

출처

alive

이전 포스트

Dynamic Programming

다음 포스트

Policy Iteration과 Value Iteration

0개의 댓글