Markov Process

미래는 현재에 의해 결정된다

현재 state는 이미 과거의 actions에 비해 축적된 결과이기에
모든 과거를 돌아보지 않고 현재만 고려하여 미래를 결정하자를 가정한다

배경지식으로...
조건부확률로 | 를 기준으로
오른쪽에 있는 일이 일어난 후에 왼쪽에 일어난 일이 발생할 확률

Markov Decision Process

MDP 구성요소

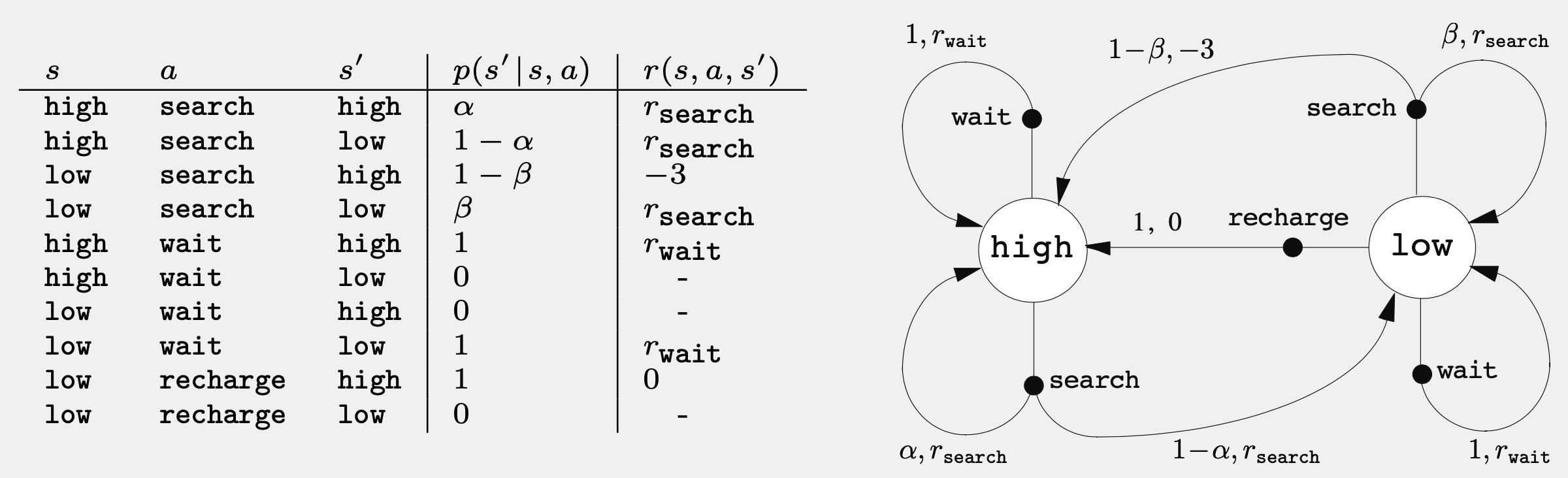
재활용 처리 로봇을 다음과 같이 표현했다
state high, low는 배터리의 현재 용량을 의미하며
action은 wait, search, recharge 3개다

• $S$ : state 집합 전체. s는 현재 상태 s'는 다음 상태를 의미.
  그림 속의 흰 동그라미

• $A$ : agent가 취할 수 있는 action 집합 전체.
  그림 속의 검은색 동그라미

• state-transition probability: 어떠한 시점 t에 state s에서 action a를 취할 경우, 다음 시점 t+1에 state s'로 전이할 확률

  • 각 state에서 다음으로 넘어갈 때 발생할 수 있는 모든 확률은 항상 총합이 1

  $P_a(s, s') = Pr(s_{t+1}=s' | s_t=s, a_t=a)$

• reward : state s에서 action a로 인해 state s'로 전이할 경우 받게되는 즉각적인 보상의 기댓값
  그림 속의 빨간 글씨

  $R^a_s = E[R_{t+1} | S_t = s, A_t = a]$

• 𝜸 : discount factor. (0<=𝜸<=1). 현재 얻게 되는 보상이 미래에 얻게 될 보상보다 얼마나 더 중요한지.

목표(Goal)와 Discount rate

여기서 목표(Goal)은 보상값을 최대로 하도록 state transition하는 것

$G_t = R_{t+1} + rR_{t+2}+r^2R_{t+3}+ ...$

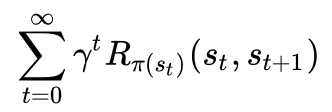
그런데 이를 s1 -> s2 -> s1-> s2 ... 만 반복하여 값을 올린다면 문제
이 때문에 과정이 길어질 수록 보상값을 줄이는 매 state마다 𝛾 를 곱해준다
이를 discount factor라고 표현. 일반적으로 1에 가까운 수로 정해진다.

만약 모든 reward가 1로 고정되었다면
오로지 Goal = 𝜸의 등비수열의 합이 되어
$Goal = \frac{1}{(1-r)}$ 이 된다

---

출처

• https://ko.wikipedia.org/wiki/마르코프_결정_과정