SARSA: On-policy TD Ctrl

Learning action-value function

On-policy에서는

현재 behavior policy $\pi$에 대한
$q_{\pi}(s,a)$를 추정한다
동시에 $\pi$가 $q_{\pi}$에 대해 더 탐욕적으로 되도록
$\pi$를 변화시킨다

$v_{\pi}$ 학습을 돌이켜 보면
episode는 state와 state-action pairs의 나열로 구성되었다
아래 그림은 이를 표현한다

이제는 state-action pair 간 transition을 고려하고
state-action pair의 value를 학습할 것이다

• $Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha [ R_{t+1} +\gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) ]$

nonterminal state ($S_t$)에서
매 transiton 이후 마다 이러한 update가 되며,
terminal state ($S_{t+1}$)에서
($Q(S_{t+1}, A_{t+1})$)는 0으로 정의한다

MC와의 비교
MC는 terminal state가 보장되지 않은 경우, (도착지/목표가 계속해서 변화한다던가)에 사용할 수 없다
이에 반해 SARSA는 이와 상관 없이
정책이 좋지 않아도 에피소드마다 빠르게 학습한다
이유는 정책을 바꿀 수 있기 때문이다

Q-learning: Off-policy TD Ctrl

학습된 Q는 자신이 따르는 정책에 상관없이
$q_*$를 직접적으로 근사한다
즉, Q는 확률 1에서 $q_*$로 수렴한다

• $Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha [ R_{t+1} +\gamma maxQ(S_{t+1}, a) - Q(S_t, A_t) ]$

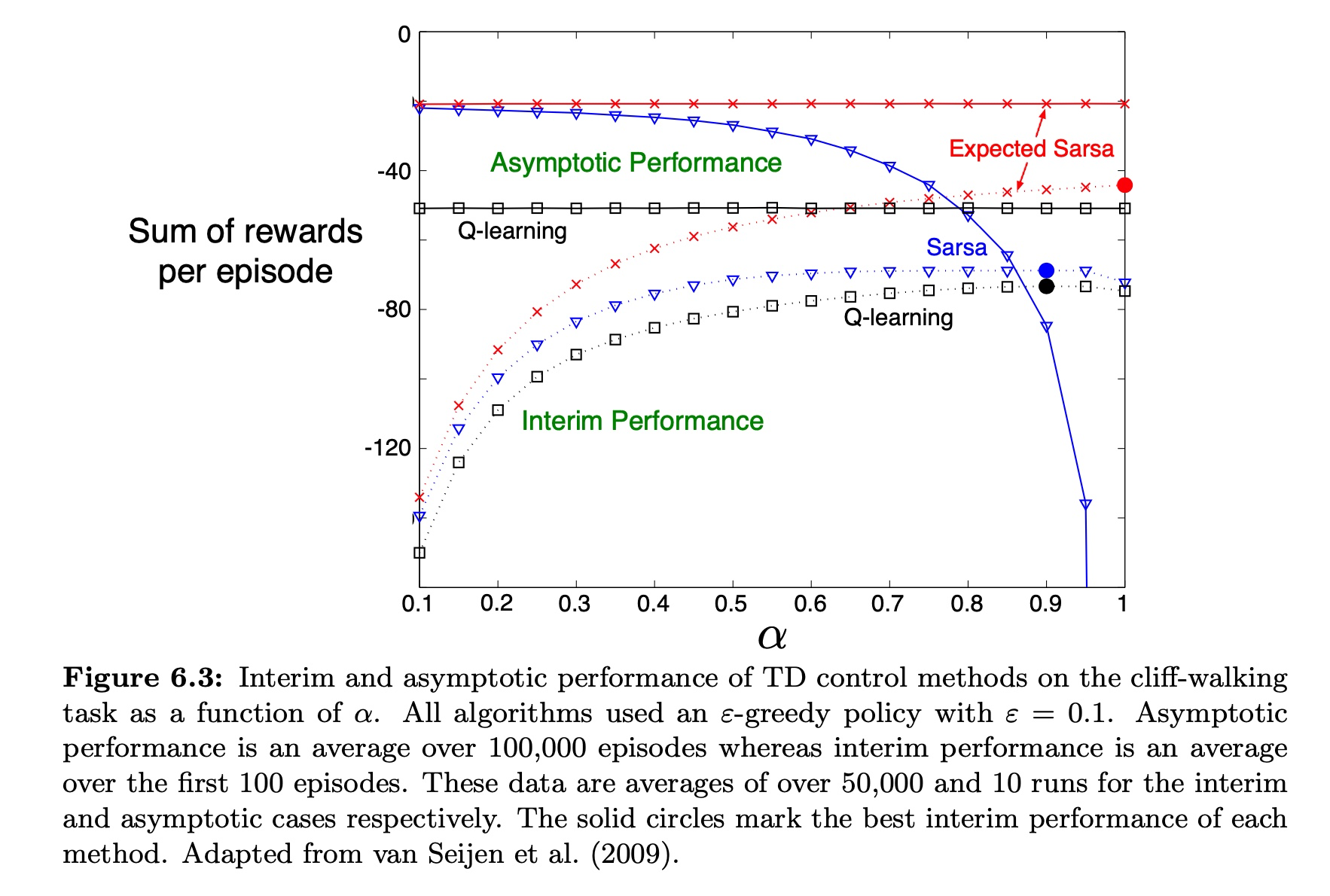
절벽 걷기 상황에서
Q learning은 optimal policy의 value를 학습하기에,
절벽 끄트머리를 따라 걷는다
그렇기에 절벽에서 떨어진 상황에 크게 감점을 받게 되고
이는 $\epsilon$-greedy action selection으로 인해 피할 수가 없다
안전한 길을 찾고자 할 때는 오래 걸리지만 SARSA를 사용해야 한다

즉, Q-learning은 On-line 성능이 낮다.

Expected SARSA

SARSA와 다르게
다음 action을 무작위로 선정하기 때문에 분산(variance)이 없어졌다.

• $Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha [ R_{t+1} +\gamma E_{\pi}[Q(S_{t+1}, A_{t+1} | S_{t+1}] - Q(S_t, A_t) ]$

SARSA는 작은 $\alpha$로 오래 돌려서 성능을 얻어야 하기 short-term 성능이 낮다.
반면에 Expected SARSA는 점점 성능이 떨어지지 않으면서 $\alpha=1$으로 설정할 수 있다.

Expected SARSA는 target policy마다 다른 policy를 사용하기에,
on-policy도 되지만 off-policy에도 적용된다.
예로, $\pi$가 greedy policy라면 좀 더 탐험에 치중하여 Q-learning에 유사해진다

Backup Diagram of TD Ctrl

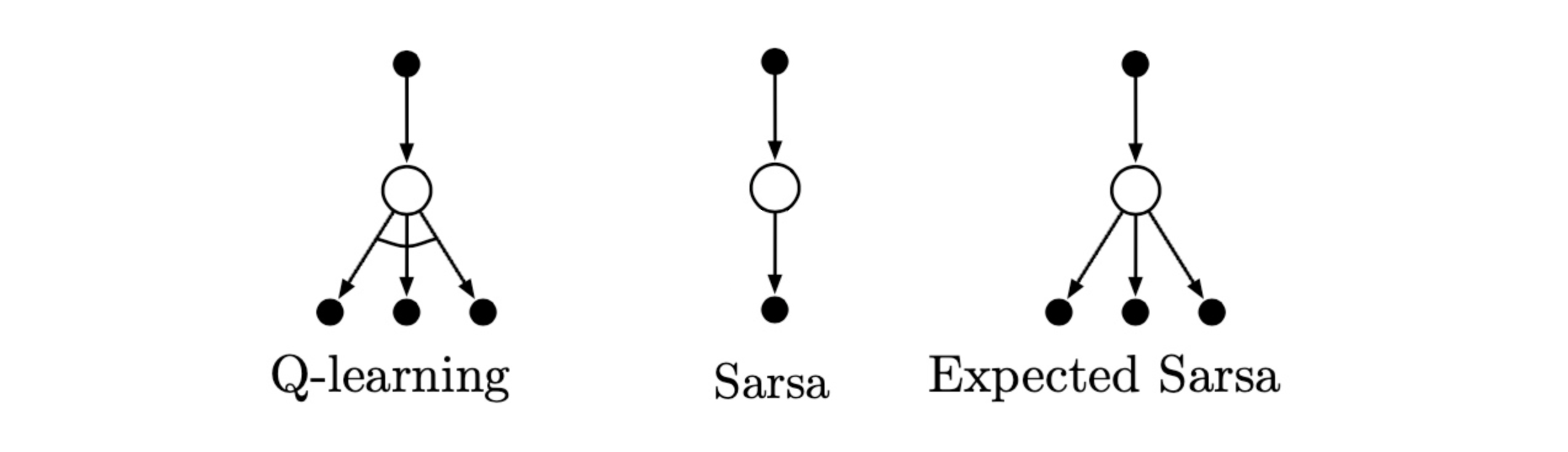
Q-learning의 식을 보면 state-action value를 갱신하므로
back-up diagram에서 root node와 leaf node는 작고 색이 칠해진 behavier node로 표시한다

Maximization Bias and Double Learning

가장 큰 추정치를, 실제값으로 고려해서 생기는 bias에 대해서 알아보자

Maximization

• 항상 가장 높은 확률을 가진 action을 선택하는 것

• Q-learning에서는 greedy policy로 최대 action value를 선택하고,

• SARSA는 $\epsilon$-greedy 는 최대화 전략을 사용한다.

• Maximization bias

  • 실제 최대값은 0이지만 추정값의 최대값이 positivie bias일 때
  • 추정값의 최대값: 추정값 너머의 최대값이 최대값을 추정한 값으로 사용

Double Learning

위와 같은 상황에서
Q-learning은 초기에 오른쪽보단 왼쪽만 선택하는 경향을 피하기 위하여
Double Q-Learning을 사용해볼 수 있다
이는 maximization bias에 영향을 받지 않기 때문이다

두 개의 추정값을 학습하고 오직 하나만 업데이트한다
이는 메모리를 두 배로 요구하지만 단계별 계산량이 늘어나지는 않는다

estimate of the true value : $q(a)$
estimate of player 1 : $Q_1(a)$
estimate of player 2 : $Q_2(a)$

maximize action of player 1: $A^* = argmax_aQ_1(a)$
maximize action of player 2: $A^* = argmax_aQ_2(a)$

estimate of value : $Q_2(A^*) = Q_2(argmax_aQ1(a))$
unbiased estimate : $E[Q_2(A^*)] = q(A^*)$

repeat ... for second unbiased estimate Q_1(argmax_aQ2(a))$

full MDP에서 확장된 개념으로, 동전 던지기 결과가 앞쪽이면 update를 실시한다.
두 개의 approximate value functions는 완전히 symmetrical하게 다뤄진다.
behavior policy는 둘 다 action-value 추정값을 사용한다.

• $Q_1(S_t, A_t) \leftarrow Q_1(S_t,A_t) + \alpha [R_{t+1} + \gamma Q_2(S_{t+1}, a)) - Q1(S_t, A_t)]$

Double Q-Learning