+) eligibility traces
다수의 시간 구간에 걸친 bootstrapping을 가능하게 해준다
여기서는 이를 제외하고 설명하려 한다.

---

n-step TD

TD(0)의 0단계 부터 MC의 종단계 까지 그 사이
몇 단계 쯤에서 자를지에 대한 고민이 필요 (truncated reward)

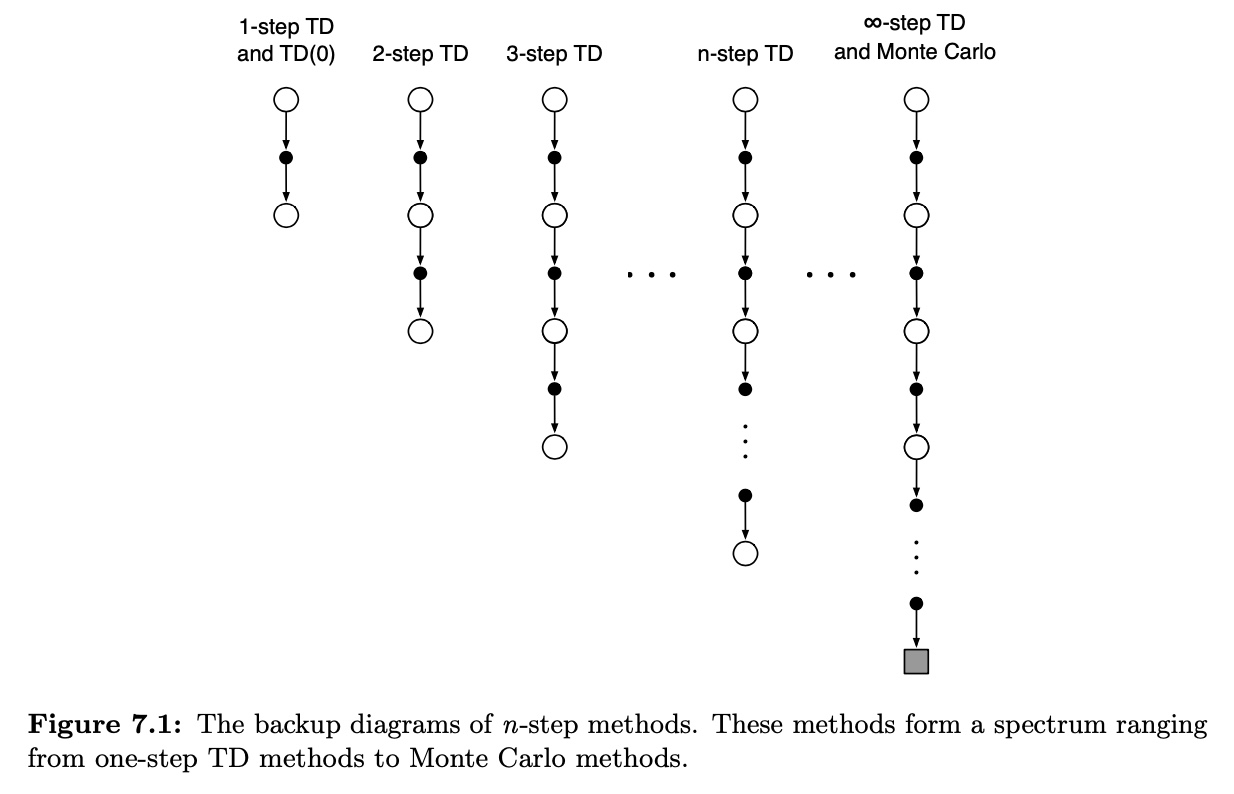
• one step return : $G_{t:t+1} := R_{t+1} + \gamma V_t(S_{t+1})$
• two step return : $G_{t:t+2} := R_{t+1} + \gamma R_{t+2}+ \gamma ^2 V_t(S_{t+2})$
  ...
• state value learning algorithm
  • $V{t+n}(S_t) := V_{t+n-1}(S_t) + \alpha[G_{t:t+n} - V_{t+n-1}(S_t)],\ \ \ \ 0\leq t \leq T$

error reduction properety
n-step return의 중요한 특성은 RETURN의 기대값이 최악의 경우에도
$V_{t+n-1}$보다 $v_{\pi}$에 대한 더 좋은 추정값임을 보장한다.

즉, N단계 이득에 대한 기댓값의 최대 오차는
$V_{t+n-1}$의 최대 오차에 $\gamma^n$을 곱한 것보다 작거나 그와 같음이 보장된다 ($n>=1$)

• $max_s | E_{\pi} [ G_{t:t+n}|S_t=s] - v_{\pi}(s)| \leq \gamma^n max_s|V_{t+n-1}(s)-v_{\pi}(s)|$

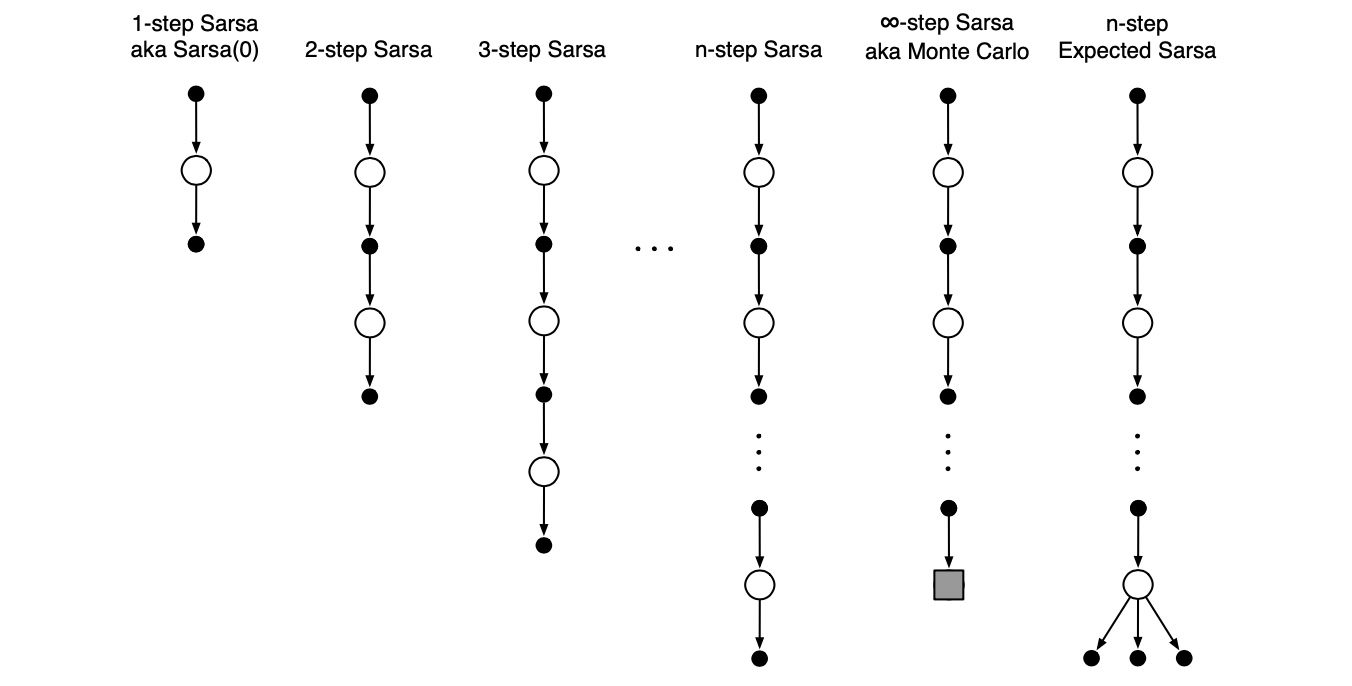
n-step SARSA (on-policy)

n-step Off-Policy Learning

off-policy learning은 policy b를 따르면서 또 다른 하나의 policy ${\pi}$에 대한 value function을 학습하는 것이다.

Off-policy version of n-step SARSA

n-step off policy를 위해, time t에서의 update에 $\rho_{t:t+n-1}$의 가중치를 적용한다.
(actually made at time $t+n$)

여기서 importance sampling ratio라 불리는 $\rho_{t:t+n-1}$는
두 정책 하에서 $A_t$로부터 $A_{t+n-1}$까지의 n개의 행동을 취할 상대적 확률

• $\rho_{t:h} := \prod_{k=t}^{min(h, T-1)} \frac{\pi (A_k|S_k)}{b(A_k|S_k)}$

importance sampling ratio는 n-step TD보다 한 단계 늦게 시작해서 한 단계 늦게끝난다.
이는 state-action pair를 갱신하기 때문.
그 행동을 선택할 확률이 얼마나 될지 신경 쓸 필요없고, 이미 선택된 행동이니 앞으로의 행동만 고려
(not $\rho_{t+1:t+n}$ but $\rho_{t+1:t+n-1}$)

• $V_{t+n}(S_t) = V_{t+n-1}(S_t) + \alpha \rho_{t:t+n-1}[G_{t:t+n-1} - V_{t+n-1}(S_t)], \ \ \ \ 0\leq t \leq T$

• $Q_{t+n}(S_t, A_t) := Q_{t+n-1}(S_t, A_t) + \alpha \rho_{t+1:t+n}[G_{t:t+n} - Q_{t+n-1}(S_t, A_t)], \ \ \ \ 0\leq t \leq T$

Per-decision Methods with Control Variates

(제어 변수가 있는 결정 단계별 방법)
여기서 $G_{h:h} := V_{h-1}(S_h)$다

일반적인 n-step에서의 goal은 $G_{t:h} = R_{t+1} + \gamma G_{t+1:h},\ \ \ \ t<h<T$

h단계에서 종료하는 n-step의 goal은 $G_{t:h} := \rho_t(R_{t+1} + \gamma G_{t+1:h}) + (1- \rho_t)V_{h-1}(S_t),\ \ \ \ t<h<T$

여기서 추가된 항은 control variate라고 부른다

control variate update의 기댓값을 변화시키지 못한다
importance sampling ratio의 기댓값은 1이고
이는 추정값과 상관관계가 없기 때문에 control variate의 기댓값은 0

control variate가 있는 off-policy의 goal은

• $G_{t:h} := R_{t+1} + \gamma (\rho_{t+1} G_{t+1:h} + V_{h-1}(S_{t+1}) - \rho_{t+1} Q_{h-1}(S_{t+1}, A_{t+1}))$
• $= R_{t+1} + \gamma\rho_{t+1}(G_{t+1:h} - Q_{h-1}(S_{t+1}, A_{t+1})) +\gamma V_{h-1}(S_{t+1})$

$h<T$이면 재귀 과정은 $G_{h:h}:=Q_{h-1}(S_h, A_h)$로 끝난다
반면, $h\ge T$면 $G_{h:h}:=R_T$로
결과적으로 만들어지는 예측 알고리즘은 expected salsa와 유사함

Off-policy Learning Without Importance Sampling: The n-step Tree Backup Alogorithm

Tree backup update

중앙 축을 따라서 세 개의 state와 reward, 두 개의 action에 이름이 표시되어 있다.
옆으로 뻗어버린 행동은 선택되지 않은 행동임을 칭한다.
선택되지 않은 행동에는 아무런 표본이 없기에 bootstrap으로 얻은 행동의value에 대한 추정값을 이용하여 goal을 설정한다

모든 단계에서 옆으로 뻗은 행동의 가치 추정값도 '추가로' 목표에 포함된다는 점이 이전과 다르다.
즉, 트리의 leaf node에 대한 행동 가치 추정값으로부터 갱신이 이루어진다.
실제로 취한 행동 $A_{t+1}$는 갱신에 참여하지 않는다.
이 행동의 확률 $\pi(A_{t+1}| S_{t+1})$은 두 번째 단계의 모든 행동에 가치에 가중치를 부여하기 위해 사용된다.
따라서 두번재 단계에서 선택되지 않은 행동 a'는 $\pi(A_{t+1}| S_{t+1})\pi(a'|S_{t+2})$의 가중치를 갖고 기여한다.
이것은 마치 다이어그램에서 행동 노드를 향하는 각 화살표가 목표 정책 하에서 행동이 선택될 확률에 따라 가중치를 부여받는 것과 같다.
그리고 행동 아래에 트리가 있으면 그 가중치는 트리에 속하는 모든 리프 노드에 적용된다.

A Unifying Algorithm: n-step $Q(\sigma)$

지금까지 살펴본 바,

• n-step salsa는 모두 sample transition으로 이루어져 있고,
• tree backup 알고리즘은 sample transition 없이 전체에 대한 모든 state-action transition으로 구성되며,
• n-step expected salsa는 마지막 state-action transition을 제외한 모든 sample transition을 갖는다.
  이들을 어느 범위 까지 통합할 수 있을까?

아래 그림은
SALSA처럼 행동을 sample처럼 취하기 원하는지, 아니면
tree backup update처럼 모든 행동에 대한 기댓값을 고려할 것인지
단계별로 결정할 수 있음을 보여준다.

항상 sample을 취하기를 원한다면 SALSA가 되고,
결코 sample을 취하지 않는다면 tree backup 알고리즘이다
expected salsa는 마지막 단계를 제외한 모든 단계에서 표본을 취하는 경우다.

자 그래서, n-step $Q(\sigma)$ 알고리즘이란 다음과 같다.
그래서 $\sigma = 1$은 whole sample을, $\sigma = 0$이면 sample 없이 순수하게 기댓값을 이용하는 것이다
$\sigma$는 0에서 1 사이로, t step에서 sample을 취하는 정도 : degree of sampling 이다.
확률 변수 $\sigma_t$는 시각 t에서 state, action, state-action pair에 대한 함수를 설정할 수 있따.