여태까지 영어로 썼었는데, 난 한국인이니까 이제부터는 한글로 써볼 것이다.

1. Introduction

기존의 생성 모델은 VAE처럼 likelihood-based이거나 GAN처럼 적대적 학습(adversarial training)을 진행하였다.

1-1. Limitations of previous generative models

그러나 위에서 언급한 생성모델들은 준수한 성능을 보였음에도 불구하고 다음과 같은 한계점을 가졌는데,

likelihood-based model

• 복잡한 확률모델의 normalizing을 위한 특수한 아키텍쳐를 만들거나
• loss를 직접적으로 구할 수 없기에 ELBO 등의 대체제를 이용해야 한다

GAN

• generator와 discriminator 사이의 균형을 항상 유지해야 하기 때문에 학습과정이 불안정할 수 있고,
• 다른 GAN 모델과 비교/평가 가 어렵다는 한계점이 있다.

Other Objectives

• 주로 낮은 차원의 데이터에서만 잘 작동한다는 단점이 있다.

따라서 위와 같은 한계점을 극복하고자 본 논문에서는 sampling 과 gradient estimation에 score-matching을 도입하고, Langevin dynamics를 활용해 새로운 샘플을 생성하는 방식을 소개한다.

1-2. What is Score?

Score-matching과 Langevin dynamics 전에 score가 무엇인지에 대해 짚고 넘어갈 필요가 있다.

생성모델의 궁극적인 목표는 주어진 데이터의 PDF(probability density function)를 학습하는 것이다. PDF를 학습하면 데이터가 어떻게 확률적으로 분포되어 있는지를 알 수 있고, 이를 통해 다른 샘플을 생성할 수 있다. pdf(주어진 데이터의 분포)는 $p_{data}(x)$로 표기한다.

Score(혹은 Score function)란, input variable 분포에 대한 log-pdf의 gradient로, 쉽게 말해 생성모델이 간단한 분포에서 복잡한 원래 분포로 돌아가는 방법을 배울 수 있도록 인도하는 가이드라인이라고 할 수 있다. Score는 $\nabla\log{p_{data}(x)}$로 표기한다.

2. Score-based generative modeling

2-1. Score estimation을 위한 Score matching

$\theta$에 의해 parametrize되어 있고, $p_{data}(x)$의 score를 추정하기 위한 neural network를 $s_{\theta}$라고 할 때, 해당 모델의 objective function은
$\frac{1}{2}\mathbb{E}_{p_{data}(x)}[||s_{\theta}-\nabla_{x}\log{p_{data}(x)}||^2_2]$를 최소화하는 것이다.

2-2. Denoising Score Matching

그러나 이전 논문들에서도 언급 되었듯이 $p_{data}(x)$를 곧바로 구하는 것은 어려운 일이다. 이때, denoising score matching을 활용한다면 $p_{data}(x)$를 예측하지 않고도 직접적으로 $s_{\theta}$를 학습시킬 수 있고, objective function은 아래와 같다.

각 항을 분해해서 살펴보자.

1. $\nabla_x s_{\theta}(x)$ : score $s_{\theta}(x)$의 Jacobian matrix

   • 데이터 $x$에 대해 score가 어떻게 변화하는지에 대한 정보를 담고 있음

2. $tr(...)$ : Jacobian matrix의 trace로, 대각선 성분의 합

   • score의 divergence
   • score가 data space의 각 point에서 얼마나 확장, 수축하는지를 나타냄

3. $||s_{\theta}(x)||^{2}_2$ : score의 L2 norm의 제곱

   • data space 각 점에서의 score의 값

4. $\mathbb{E}_{p_{data}(x)}[...]$ : 모든 data point에 대한 평균

2-3. Langevin Dynamics

Denoising score matching이 모델을 학습하는데 쓰인다면, Langevin dynamics는 샘플을 생성해내는데 사용되는데, p(x)로부터 score만을 사용한다는 점에서 의미가 있다. Langevin은 아래 식처럼 반복적으로 score를 더해주는 방식으로 sampling이 진행된다.

Step size는 $\epsilon$으로 고정하고, 초기 값을 $\tilde{x}_0 \sim\pi(x)$로 설정한다. 이때, $\pi$는 prior distribution이다. Prior distribution은 가장 단순한 분포, 즉, 완전히 preturb된 데이터를 의미하고, 여기서 위 식을 반복하며 데이터를 복구해나가면서 원래의 복잡한 분포를 찾아나간다.

• Langevin 동역학은 분자 시스템의 움직임을 수학적으로 모델링한 것이라는데, 여기서 원리를 가져왔다 정도만 알아도 이해하는데 큰 문제는 없었던 것 같다.

3. Challenges

Score-based generative modeling은 다음과 같은 문제점들을 극복해내야했다.

3-1. The manifold hypothesis

Manifold?

고차원 데이터가 어떠한 패턴이나 구조를 가지며 낮은 차원의 manifold를 형성한다.

Manifold Hypothesis

실제 데이터가 고차원에 임베딩 되어 있는 낮은 차원의 manifold에 집중되어 있는 경향을 보인다. 본 논문에서는 Manifold Hypothesis로 인한 두 가지 어려움을 제시하는데,

1. score가 고차원에서 구한 gradient이기 때문에 x가 저차원의 manifold에 국한되어 있는지 알 길이 없다.
2. data가 mainfold에 속해있을 경우, score matching objective는 불안정한 score 값을 제시하게 된다.

따라서 이를 해결하기 위해서 data에 아주 약간의 noise(육안으로 구분되지 않는 정도)를 더해준다.

• Manifold에 속해있는 data에 noise를 추가해줌으로써 Manifold에 국한되지 않게 하고,
• 기존 data를 거의 손상시키지 않았기 때문에 feature를 학습하는데는 지장이 없다.

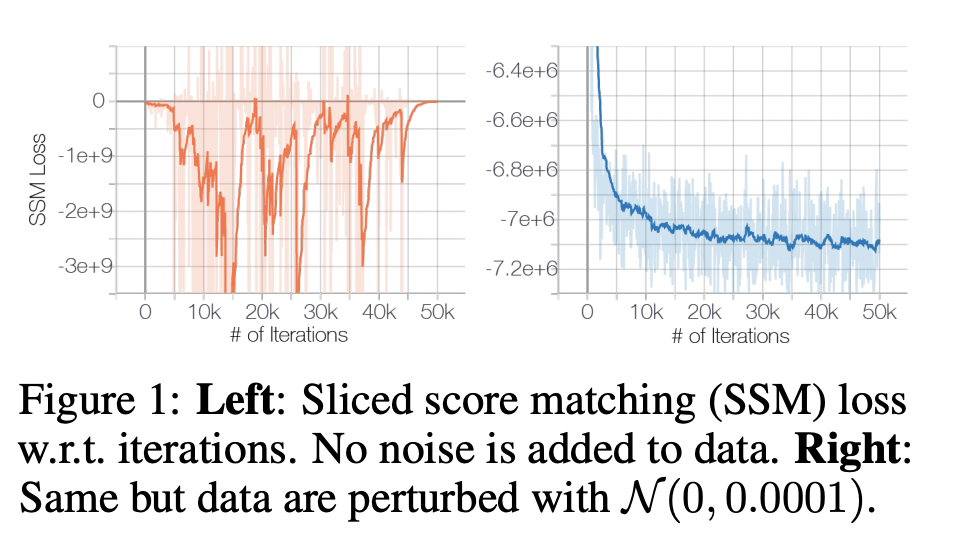
3-2. Low Data Density Regions

Data의 밀도가 낮은 부분에서는 score estimation과 Langevin Dynamics를 활용한 sampling이 어려울 수 있다.

4. Noise Conditional Score Networks: learning and inference

3에서 발생했던 문제들을 해결하기 위해서

1. 각각 다른 레벨의 noise를 추가하여 data를 손상시킨다.
2. 동시에 모든 noise 레벨에 해당하는 score를 예측하고 하나의 score network를 훈련시킨다.

1,2를 통해 학습을 마친 후 Langevine Dynamics를 이용해서 sampling한다.

4-1. Training

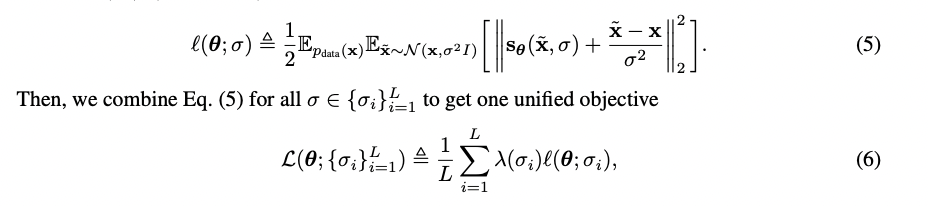
4-2. Inference