선형대수학 - 수학적 벡터

Hyewon Jung·2023년 7월 16일

출처
이상엽 MATH

0. 용어정리

대수학의 대상 : 수 뿐만 아니라 수를 대신할 수 있는 모든 것.
대수학 : 대수구조를 연구하는 학문
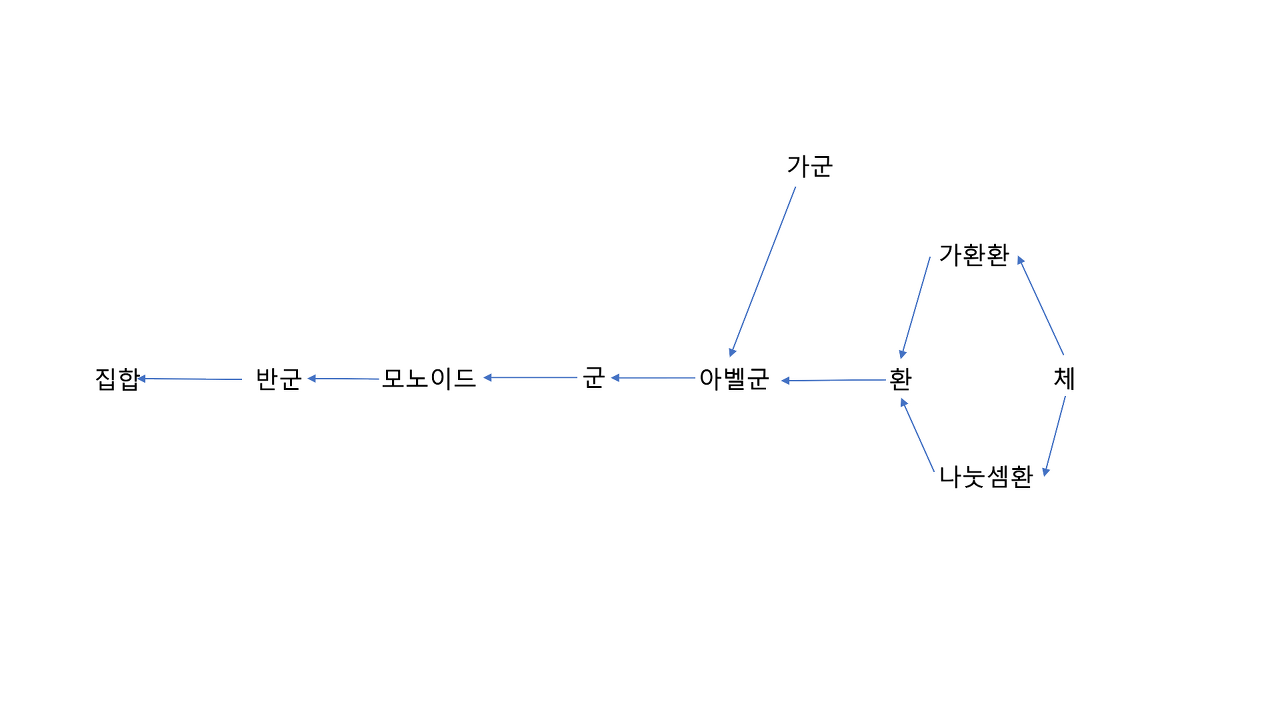
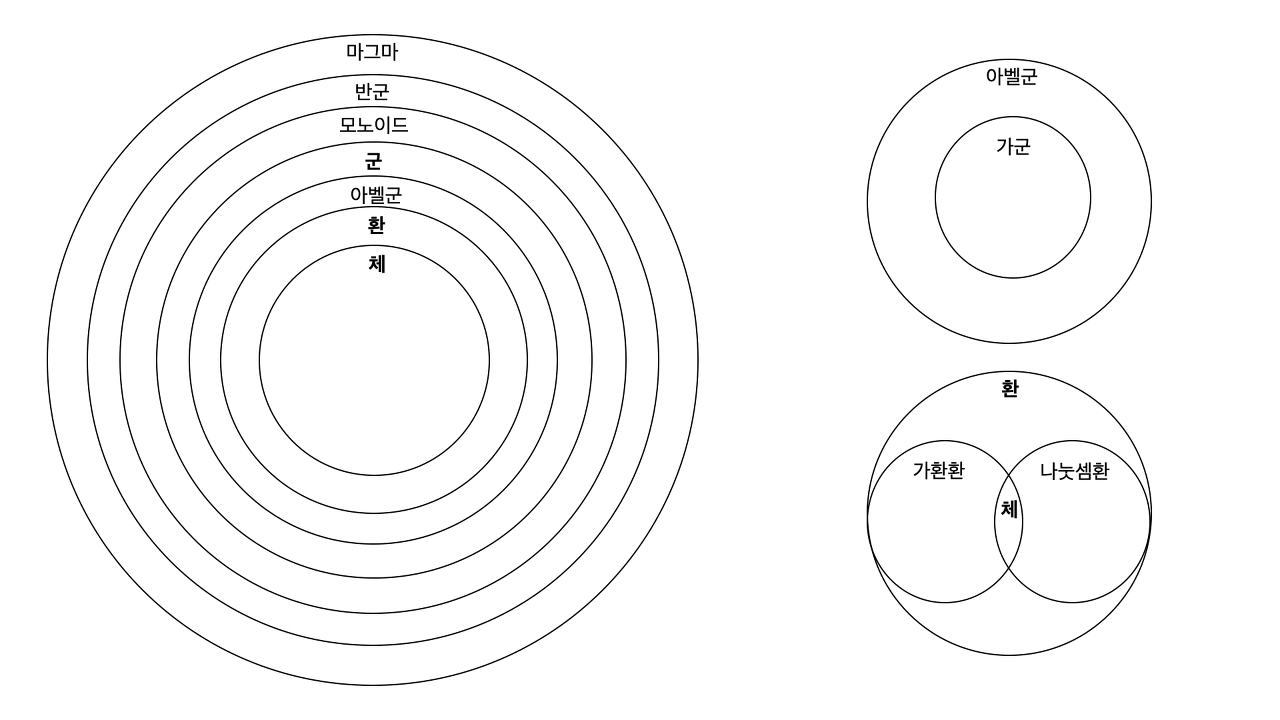
대수구조 : 집합, 집합에 부여된 연산
- 반군(결합법칙) : 집합과 그 위의 결합법칙을 따르는 하나의 이항 연산을 갖춘 대수구조
- 모노이드(결합법칙, 항등원) : 항등원을 갖는 반군 반군이므로 결합법칙도 성립한다.
- 군(결합법칙, 항등원, 역원) : 역원을 갖는 모노이드
- 아벨군(결합법칙, 교환법칙, 항등원, 역원)
- 환(결합법칙, 교환법칙, 항등원, 역원|결합법칙)
- 가군
- 가환환(결합법칙, 교환법칙, 항등원, 역원|결합법칙, 교환법칙)
- 나눗셈환(결합법칙, 교환법칙, 항등원, 역원|결합법칙, 항등원, 역원)
- 체(결합법칙, 교환법칙, 항등원, 역원|결합법칙, 교환법칙, 항등원, 역원)

반군

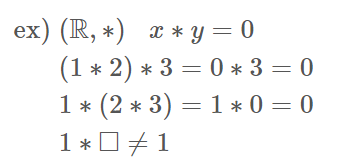
위의 대수구조는 결합법칙이 성립함 = 반군임
항등원은 존재하지 않음 = 모노이드는 아님

군

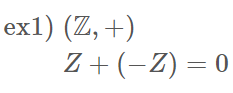
역원을 가지므로 군

1. 벡터공간

1) 벡터공간

벡터공간 : 체 F에 대한 가군 $(V, + , \cdot)$
- 체도 환의 하위구조이기 때문에 가군이라고 부를 수 있다.
벡터 : 아벨군 V의 원소
스칼라 : 체 F에서 떼온 원소
+, $\cdot$ 는 벡터공간에 부여된 어떤 연산을 의미한다.
- 이 때 +는 벡터의 덧셈이고 $\cdot$ 은 벡터의 스칼라배다
- 연산은 기본적으로 함수이다. +라고해서 더하기인가?라고 생각하면 안된다는 것. f(x)처럼 +라는 기호의 함수이다. 그러나 기본적인 성질은 존재한다.
- + : VxV -> V인 함수 (정의역 : V끼리의 곱집합)
- $\cdot$ : FxV -> V인 함수 (정의역 : F와 V간의 곱집합)
- 곱집합 : 집합 안의 원소들끼리 만들어질 수 있는 모든 집합의 개수

(1) 특징

벡터공간은 구조상 가군의 일종.
아벨군을 본체로 하고 환의 하위구조인 체의 원소를 받아 곱셈이 정의된 대수공간.
가군은 본래 환에서부터 원소를 가져오지만 스칼라를 정의함에 있어서 환까지 필요없기 때문에 체에서 가져온다.
본체에 있던 아벨군 원소 = 벡터
체의 원소 = 스칼라
스칼라를 왜 체에서 가져오느냐? 체는 복소수, 유한체, 실수 등의 집합이고 스칼라는 실수의 집합으로 구성되기 때문이다.
벡터가 유일하게 존재하면 의미가 없다. 둘 이상의 벡터가 있어야 크기와 방향을 논할 수 있다. 크기와 방향은 상대적인 것이기 때문이다.
이 두 벡터의 방향이 서로 같냐 다르냐는 하나의 벡터를 줄이거나 늘이거나해서 다른 벡터와 일치시킬 수 있느냐의 문제로 전환된다.
어떤 한 벡터를 줄이거나 늘이거나 = 스칼라배
그러므로 아벨군 하나에 부여된 덧셈이 아니라 체까지 확장해서 스칼라배까지 정의해줬을 때 완전체가 된다.

(2) 벡터집합으로 불리기 위한 공리, 조건

V라는 집합에 대해 덧셈구조가 부여되었을 때 (V, +)는 아벨군을 형성해야된다. = 1)결합법칙, 2)교환법칙, 3)항등원, 4)역원을 성립해야된다.
체에서부터 원소하나를 부여받아 스칼라배 ( $\cdot$ )가 정의가 되었을 때, $(V, + , \cdot)$ 의 대수구조가 F에 대한 가군을 성립해야된다. = 1)교환법칙, 3)분배법칙 성립, 2)항등원에 대한 계산구조 성립해야된다. 이때 3번의 +는 일반 사칙연산기호이다. 함수가 아님!

=> 벡터공간임을 확인하기 위해서는 위의 모든 공리를 만족해야 한다.

(3) 벡터공간 예시

예시가 다음과 같을 때

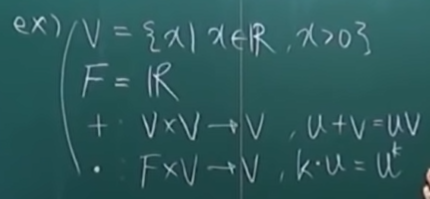
v는 벡터
+는 특수하게 정의된 함수. 여기서는 u+v하겠다 = uv다.

1. $(V,+)$ 가 아벨군인지 확인

: 벡터공간으로 정의되기 위한 공리 1번을 만족하는지 확인

1) (u+v)+w = (uv) + w를 만족해야 함

앞서 정의한 +는 곱하기를 하는 함수였음.

-> (uv)+w가 됨

-> uv의 결과가 k원소라고 하면 k+w 는 또 +함수에의해 kw가 됨

-> 결국 (uv)+w = uvw처럼 됨

-> 반대도 마찬가지 + 기호가 곱하기 함수이기 때문임

2) u+v = uv = vu = v+u
-> +는 곱하기처럼 사용됨.

3) u + 1 = u1 = u
: 임의의 실수 u에 무언가(여기선 1)을 덧셈연산한 결과 u가 나옴, u에 x를 더해서 똑같은 u가 결과로 나왔기 때문에 이를 통해 1은 항등원 역할을 하는 것을 알 수 있다. (물리적벡터에서의 0벡터가 여기서는 1로 치환된 것이라고 생각하면 된다.)

4) u + $1 \over u$ = u $\times$ $1 \over u$ = 1
: 무언가( $1 \over u$ )를 더했더니 1이 나온다 $1 \over u$ << 이건 u의 역원일 수밖에 없음. 또한, u를 양의 실수 집합으로 잡았으므로 u의 역수도 양의 실수 집합 내부에 있을 것임.

=> 위 네가지 공리를 만족함. 즉, 아벨군 형성이 되었음을 알 수 있음

2. $(V, + , \cdot)$ 가 가군이 형성되는지 확인

1) $k(mu) = k u^m = (u^m)^k = u^{mk} = u^{km} = (km)*u$

-> $\cdot$ 함수를 지수로 정의하였음.
-> 그래서 m이 지수로 올라감
-> 그리고 k도 지수로 올라감
-> 지수 km을 다시 앞으로 빼줄 수 있음.

2) $1u$ = $u^1$ = u

3) $(k+m)\cdot(u+v)$

: 이 때 k와 m의 +는 벡터끼리에만 적용되는 함수이고 k와 m 둘 다 스칼라이므로 여기선 사칙연산의 +임을 주의해야 한다. u와 v의 경우 벡터이므로 정의된 함수처럼 곱해주면 된다.

-> 벡터끼리의 연산만 +가 곱하기처럼 들어감 여기선 스칼라끼리(F)의 곱이기 때문에 일반 +부호

-> 그래서 k+m은 일반 더하기, u+v는 둘 다 벡터이므로 곱하기처럼 해줌

= (u+v)^{k+m} = (uv)^{k+m} = u^{k+m}v^{k+m} = u^ku^mv^mv^k

: 이때, u와 v는 V의 원소이므로 벡터이다. 그러므로 +는 함수이다. 그렇기 때문에 새로 정의된 함수처럼 +로 식을 아래와같이 나눠줄 수 있는 것이다.

= u^k + u^m + v^k + v^m = ku + mu + kv + mv = ku+mu+kv+mv

위 두가지를 확인해봐야 한다. 두가지를 만족하면 벡터공간이다. 즉, 예시의 집합과 스칼라는 벡터공간이다.
이 벡터공간을 정의하고 만족하는지 확인하는 것이 중요한 이유는 물리적벡터에서 살펴본 벡터가 아닌 벡터공간의 원소인 벡터를 정의하고 사용하고자 하기 때문이다.

2) 선형생성

(1) 부분벡터공간

: 벡터공간 및 다른 대수구조들 모두 집합에서부터 비롯되었으므로 부분집합처럼 부분적으로 존재할 수 있다. 벡터공간 또한 대수구조(아벨군, 체)등으로 이루어져 있으므로 부분벡터공간이 존재할 수 있다. 이때, 벡터공간 V상에서 정의된 덧셈과 스칼라배에 대해 그 자체로써 벡터공간이 되는 V의 부분집합 W를 V의 부분벡터공간이라고 한다.

(2) (선형)생성 >> ????

: 벡터공간 V의 공집합이 아닌 부분집합 $S = \lbrace v_1, v_2, ..., v_n \rbrace$ (v들은 전부 벡터공간 V의 원소들이므로 당연히 S또한 벡터이다.) 내의 벡터들의 가능한 모든 선형결합(일차결합 v에 k배하고 덧셈뺄셈하던)으로 이루어진 V의 부분벡터공간을 S의 (선형)생성(span(S))라 한다.

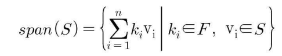
-> 이때 S가 span(S)를 생성한다.라고 말함

예시)

S = \lbrace (1,0), (0,1) \rbrace

F = R(실수 전체 집합)

span(S) = \lbrace k(1,0) + m(0,1) | k,m \in F \rbrace = \lbrace (k,m) |k,m \in F \rbrace

-> F는 실수 집합, k,m은 F에서 왔으므로 k와 m도 실수

-> 즉, (k,m)은 $R^2$

-> 즉, s라는 집합은 2차원 벡터공간 혹은 유클리드 공간을 생성한다.

-> 의미해석 : 2차원 실수 벡터 공간이 이루어지는 데 있어서 S의 두 벡터가 가장 근본적인 역할을 할 수 있다.

(3) 선형독립

: 집합 내의 벡터들이 상호연관성이 있느냐고 묻는 개념이다.

응용할 때 중요
왜? 얼마나 계산이 복잡한지 알 수 있기 때문

즉,

k_1v_1 + k_2v_2 +...+k_nv_n = \overrightarrow 0

을 만족하는 $k_n$ 의 해가 0뿐이 없다면 집합 S를 선형독립집합이라고 한다.

선형종속

: S는 선형종속집합이다.
-> 0이 아니라 다른 해가 존재하기 때문에

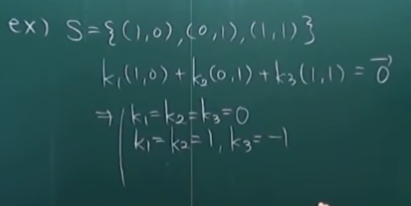
선형독립

: S는 선형독립집합이다. 선형독립집합일 때 계산도 간단하고 결과도 간단하게 나온다.

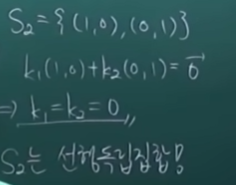
3. 여러 벡터 공간

(1) 노름공간

: 노름이 부여된

K-벡터공간(V, ||\cdot||)노름이란

∀u, v \in V, ∀ k \in K

에 대해 아래 세 조건을 만족시키는 함수를 의미한다.

앞서 살펴본 벡터공간이 벡터의 크기에 대한 내용이 누락되어 있기 때문에 노름공간에서 크기를 커버함
기본 벡터구조에 벡터 크기를 넣지 않은 이유는 내적공간이라는 것이 노름공간의 상위공간이기 때문에 벡터를 정의하는데는 관여하지 않지만 벡터들로부터 의미있는 결과를 도출하기 위한 내적공간으로부터 노름공간이 유도되기 때문에 앞서 살펴보지 않았음.
원래 벡터공간은 체에서부터 원소를 받아 F라고 정의되었는데 여기선 K라고 붙여놓았음
실수집합과 복소수집합만 K로 하기 위해서 다른 기호를 사용함
왜 실수와 복소수로 한정짓느냐 : 노름공간의 모태인 내적공간이 여기서 정의되기 때문
V라는 벡터공간에 $||\cdot||$ 이라는 연산을 부여해준 것
$\cdot$ 은 이자리에 원소가 들어간다. V의 원소가 들어감
노름은 세가지 조건을 만족시키는 함수
V는 0에서부터 무한대까지의 실수로 잡힌다.

1) k라는게 곱해지면 밖으로 절대값으로 뺄 수 있다

||kv|| = ||k||||v||

2) 두 벡터를 더한다음에 노름 계산할 때랑 두벡터 노름을 계산하고 더할 때 방향이 같지 않는 이상 후자가 더 클 것임.

3) 벡터 v의 노름이 0이다 = 벡터가 0벡터이다.

2) 내적공간

: 기본적으로 벡터공간에 추가적으로 내적연산을 한 것

이 내적공간이 왜 노름공간의 상위구조이냐면
벡터가 자기자신에 대해 두번 내적을 해준뒤 그것에 대해 루트를 씌우면 노름이 됨
노름 -> 내적을 만들려면 조건이 하나 더 붙음
내적 -> 노름은 쉽지만 노름 -> 내적은 어렵기 때문에 상위호환이라고 부름
$<\cdot, \cdot>$ 은 내적연산기호(범용적)를 의미함
이 내적공간은 실수, 복소수 집합으로 한정됨
3번의 위의 바 표시는 켤레복소수 표시
$<v, v>$ 는 자기자신에 대한 내적 -> v의 놈의 제곱

1번예시

<(1,0) + (0,1), (2,3)>

= <(1,1), (2,3)> = 1\cdot2 + 1\cdot3 = 5

<(1,0),(2,3)> + <(0,1), (2,3)>

= 1\cdot2 + 0\cdot3 +0\cdot2 + 1\cdot3 = 5

3) 유클리드 공간

: 단순히 n차원의 실수공간
: 음이 아닌 정수 $n$ 에 대하여 $n$ 차원 유클리드 공간 $R^n$ 은 실수집합 $R$ 의 $n$ 번 곱집합이며, 이를 $n$ 차원 실수 벡터 공간으로써 정의하기도 한다.

이 위의 내적

<u, v> = \displaystyle\sum_{i=1}^{n}{(u_iv_i)} = u \cdot v

을 정의하면 점곱, 스칼라곱이라고도 한다.

4. 기저와 차원

0) 차원

: 차원이란 해당 벡터공간의 기저의 원소의 개수

1) 기저

벡터공간 V의 부분집합 B가 선형독립이고 V를 생성할 때, B를 V의 기저라 한다.

(1) 정규기저

: 다음을 만족하는 노름공간 V의 기저 B를 정규기저하고 한다.

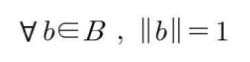
노름공간 V의 모든 원소 ∀b(b는 벡터) 의 노름값이 1이 나와야 함.

(2) 직교기저

: 다음조건을 만족하는 내적공간 V의 기저 B를 직교기저라 함

기저란 집합에서 서로다른 $b_1, b_2$ 를 가져옴
그리고 이 $b_1, b_2$ 의 내적결과는 0이 나와야 한다.
내적결과가 0이 나온다 = cos90도 = 직교한다.

(3) 정규직교기저

: 앞의 두개를 모두 만족

각이 90도라 0이 나오고
모든 벡터(원소)들의 노름 값이 1
그래서 다음과 같이 표시되는 기저를 표준기저라고함.

\lbrace (1,0,0,...), (0,1,0...,0),..., (0,0,...,1) \rbrace =

\lbrace e_1, e_2, ..., e_n \rbrace

예시

V = R^2

B_1 = \lbrace (1,0), (0,1) \rbrace

span(B_1) = k(1,0) + m(0,1) = (k,m) = R^2

1) $B_1$ 이 선형독립 집합인가?
A. yes 둘을 0으로 만들어주는건 0뿐임

2) B로 V를 k,m으로 생성도 함.

=> 그러므로 B는 V의 기저다.

예시2

S = \lbrace (1,0),(0,1),(1,1) \rbrace

는 기저인가 아닌가.

A. 아님
생성은 가능한데 선형종속임.

예시3

다음 B들은 정규기저, 직교기저가 되는가

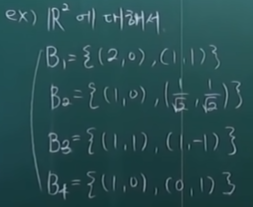
$B_1$ : 정규기저안됨, 직교기저안됨

-> 처음 벡터 b의 노름이 2가 나옴

-> 내적결과가 $2\cdot1+0\cdot1 = 2$

$B_2$ : 정규기저됨, 직교기저안됨

$B_3$ : 정규기저안됨, 직교기저됨

$B_4$ : 정규기저됨, 직교기저됨 => 표준기저임

Hyewon Jung

Amateur data scientist & student

이전 포스트

선형대수학 - 벡터

다음 포스트

선형대수학 - 수학적 벡터

0. 용어정리

반군

군

1. 벡터공간

1) 벡터공간

(1) 특징

(2) 벡터집합으로 불리기 위한 공리, 조건

(3) 벡터공간 예시

1. $(V,+)$ 가 아벨군인지 확인

2. $(V, + , \cdot)$ 가 가군이 형성되는지 확인

1) $k(mu) = k u^m = (u^m)^k = u^{mk} = u^{km} = (km)*u$

2) $1u$ = $u^1$ = u

3) $(k+m)\cdot(u+v)$

2) 선형생성

(1) 부분벡터공간

(2) (선형)생성 >> ????

예시)

(3) 선형독립

선형종속

선형독립

3. 여러 벡터 공간

(1) 노름공간

2) 내적공간

1번예시

3) 유클리드 공간

4. 기저와 차원

0) 차원

1) 기저

(1) 정규기저

(2) 직교기저

(3) 정규직교기저

예시

예시2

예시3

선형대수학 - 벡터

선형대수학 - 고윳값과 대각화

0개의 댓글

선형대수학 - 수학적 벡터

0. 용어정리

반군

군

1. 벡터공간

1) 벡터공간

(1) 특징

(2) 벡터집합으로 불리기 위한 공리, 조건

(3) 벡터공간 예시

1. (V,+)(V,+)(V,+)가 아벨군인지 확인

2. (V,+,⋅)(V, + , \cdot)(V,+,⋅) 가 가군이 형성되는지 확인

1) k∗(m∗u)=k∗um=(um)k=umk=ukm=(k∗m)∗uk*(m*u) = k *u^m = (u^m)^k = u^{mk} = u^{km} = (k*m)*uk∗(m∗u)=k∗um=(um)k=umk=ukm=(k∗m)∗u

2) 1u1u1u = u1u^1u1 = u

3) (k+m)⋅(u+v)(k+m)\cdot(u+v)(k+m)⋅(u+v)

2) 선형생성

(1) 부분벡터공간

(2) (선형)생성 >> ????

예시)

(3) 선형독립

선형종속

선형독립

3. 여러 벡터 공간

(1) 노름공간

2) 내적공간

1번예시

3) 유클리드 공간

4. 기저와 차원

0) 차원

1) 기저

(1) 정규기저

(2) 직교기저

(3) 정규직교기저

예시

예시2

예시3

선형대수학 - 벡터

선형대수학 - 고윳값과 대각화

0개의 댓글

1. $(V,+)$ 가 아벨군인지 확인

2. $(V, + , \cdot)$ 가 가군이 형성되는지 확인

1) $k(mu) = k u^m = (u^m)^k = u^{mk} = u^{km} = (km)*u$

2) $1u$ = $u^1$ = u

3) $(k+m)\cdot(u+v)$