back propagation

오차 역전파 법은 딥러닝에서 학습을 수행하는데 있어 반 필수적인 방법이다.
backpropagation은 가중치 파라미터에 대한 loss function의 기울기를 손쉽게 구할 수 있도록 해준다.
여기까지가 일반적으로 알고있는 사항이다.
그렇지만 여기서 수식적으로 back propagation이 작동한다는 것인지 궁금했고, '손쉽게'란 말을 더 이해하고자 하였다.

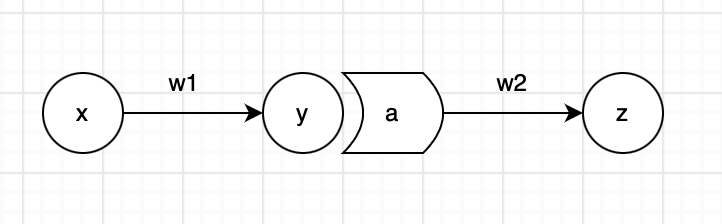
위와 같은 neural net이 있다고 생각해보자.
여기서 activation function은 sigmoid를 사용하였고, loss function은 MSE를 사용하였다.

activation function : $sig(x) = {1 \over 1 + e^{-x}}$
loss function : $E = (z-{\hat z})^2$

여기서 back propagation이 목표하는 바는, 작은 가중치 변화 ${\rm d}w_2$에 loss function $E$가 얼마나 민감하게 반응하는 지를 찾아내는 것이다.

Chain rule에 의하여, weight parameter $w_1, w_2$에 대한 loss function의 기울기는 다음과 같이 표현할 수 있다.

${\partial E \over \partial \omega_2}$
${\partial E \over \partial \omega_1} ={\partial E \over \partial a}{\partial a \over \partial y}{\partial y \over \partial w_1}$

이때 ${\hat z}=a \cdot w_2 + b_2$ 이므로,

${\partial E \over \partial a} =2(z-w_2 \cdot a) \cdot (-w_2)$
이다. 나머지 도함수도 비슷하게 구할 수 있다.
${\partial a \over \partial y}=sig(y) \cdot (1-sig(y))=a\cdot (1-a)$
${\partial y \over \partial w_1} = x$
${\partial E \over \partial w_2}=2(z-w_2 \cdot a)\cdot (-a)$

이제 weight parameter $w_1, w_2$에 대한 loss function의 기울기를 구했다.
bias에 대한 loss function의 기울기도 마찬가지의 방식으로 얻을 수 있다.
이 의미는 loss function에 대한 parameter의 민감성 혹은 중요도를 알 수 있다는 점이며, learning rate 만큼 움직이려는데 각각의 parameter를 어느 정도 움직여야 하는지를 알 수 있다는 것이다.