🔗참고링크🔗
논문: https://arxiv.org/pdf/2404.19756
깃허브: https://github.com/mintisan/awesome-kan
유튜브: https://youtu.be/myFtp5zMv8U?si=TKdMi_-GRMmksg0h
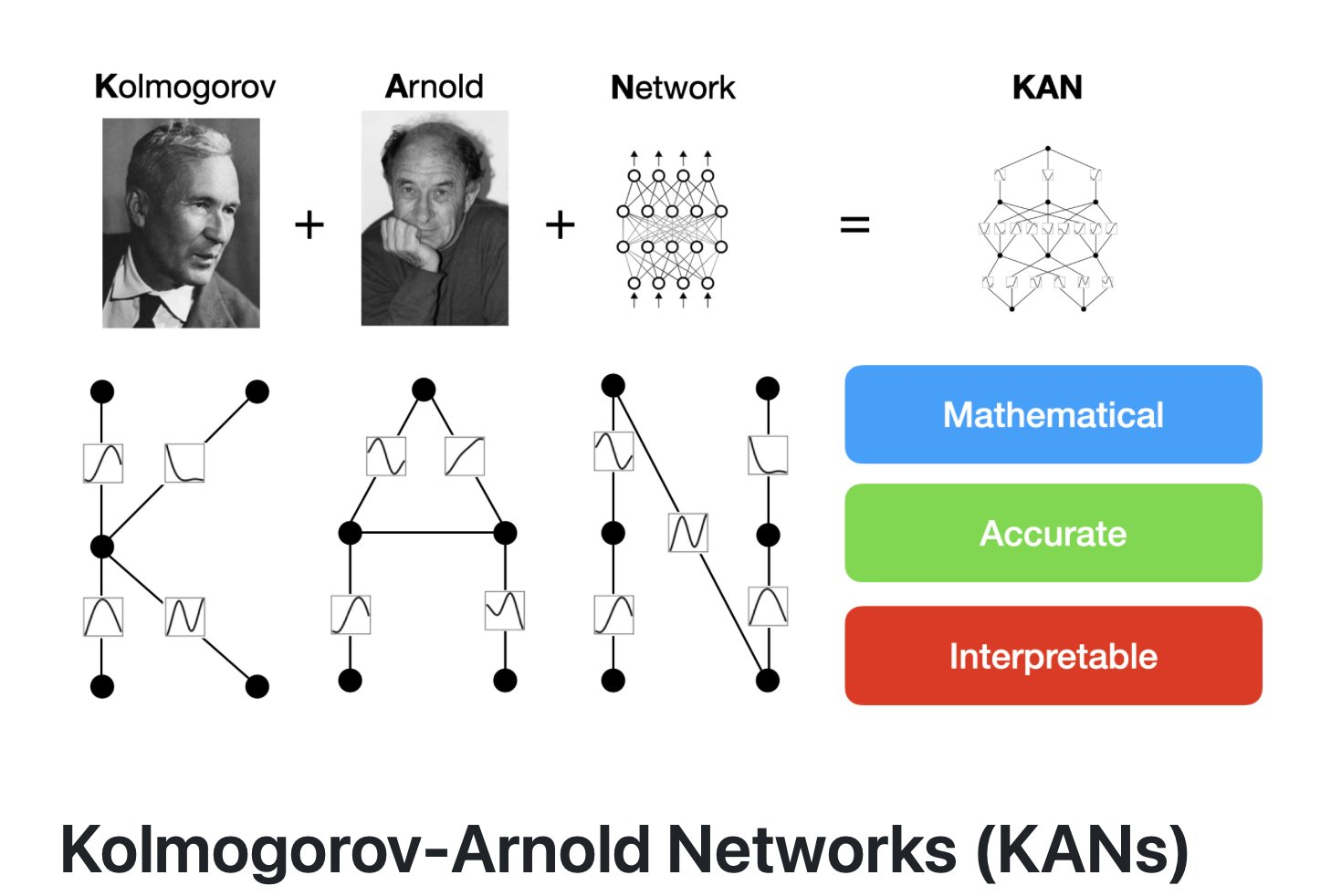
Overview
KAN은 MLP과 달리 weight을 훈련하는 것이 아니라, 활성화 함수를 훈련하는 것이다.
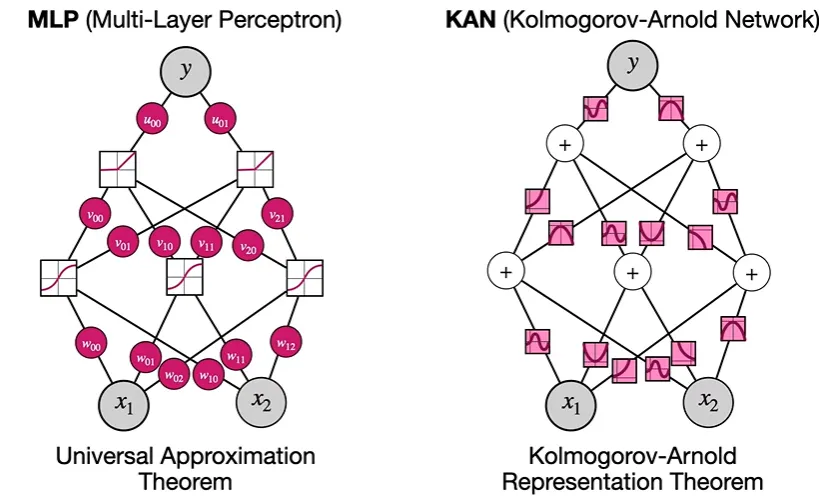
MLP vs KAN
다음 그림은 MLP와 KAN을 비교한 것이다.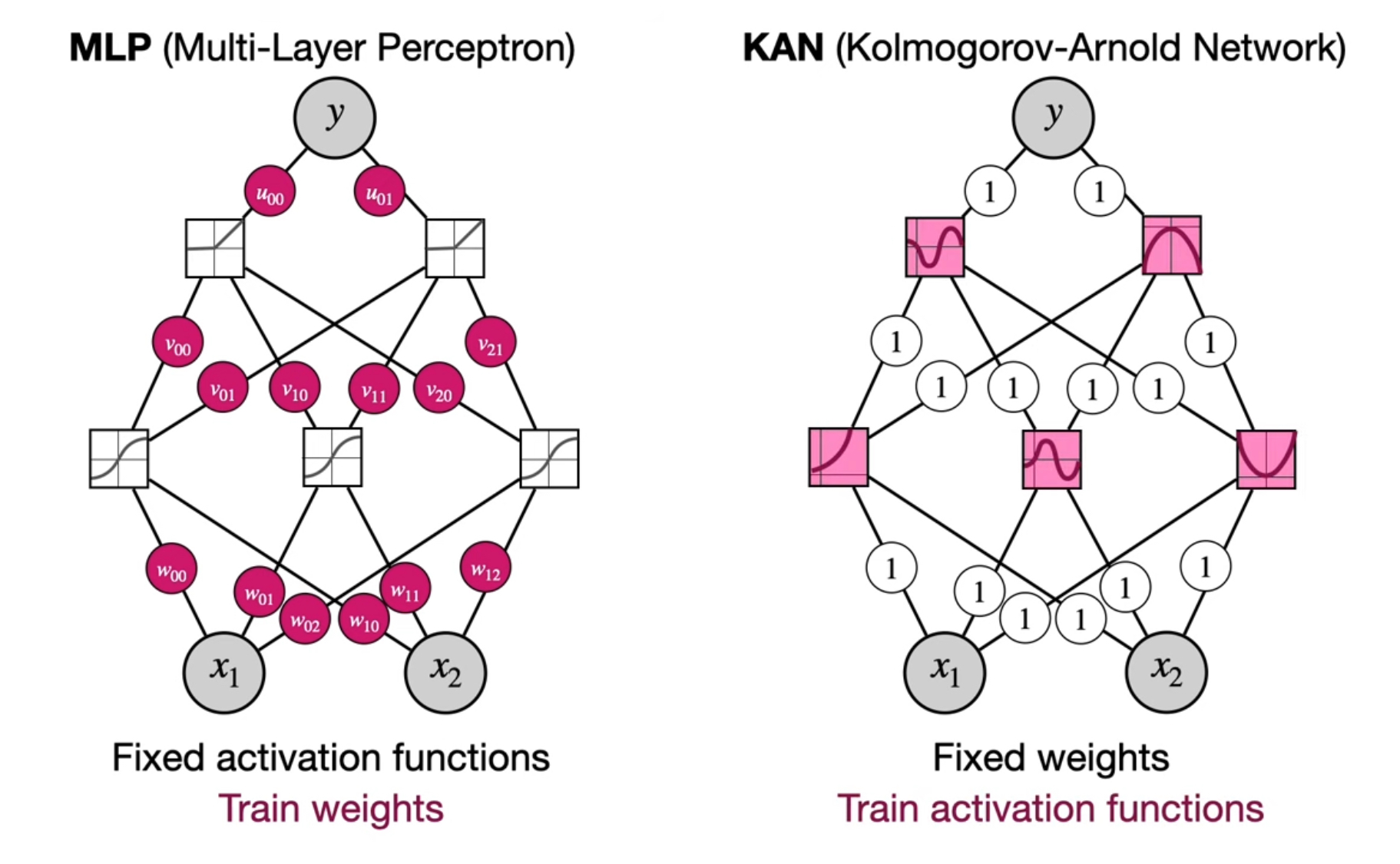
- MLP는 weight을 training한다.
KAN은 weight=1이고 활성함수를 training한다. - KAN은 가장 완벽한 모델을 이루는 activation function을 찾는 것이 목표이다.
더 정확한 KAN 모습:
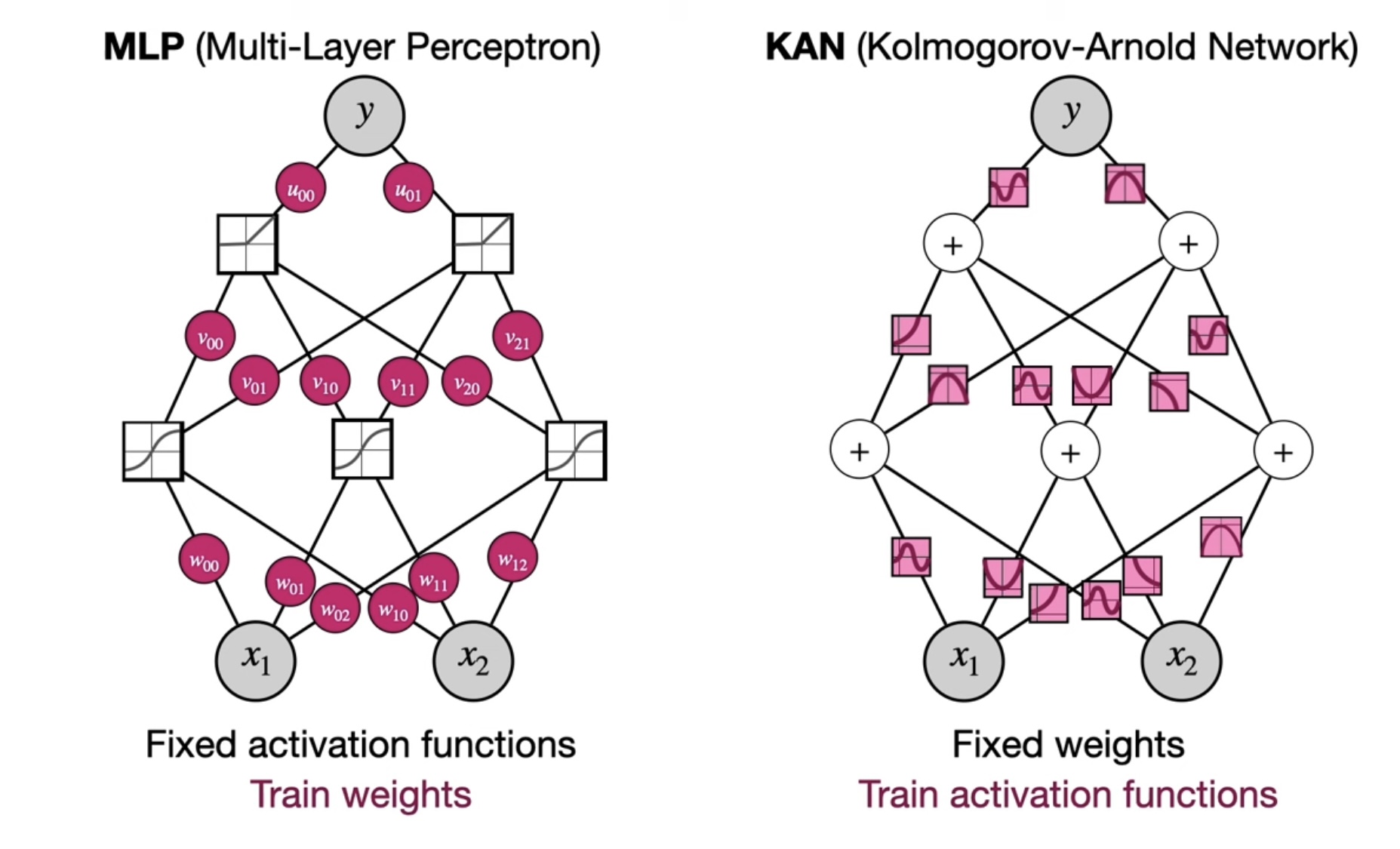
- 각 노드는 +, 엣지는 활성함수이다.
위 그림이 무슨 뜻인지, 각각의 부분 노드를 살펴봄으로써 이해해보겠다.
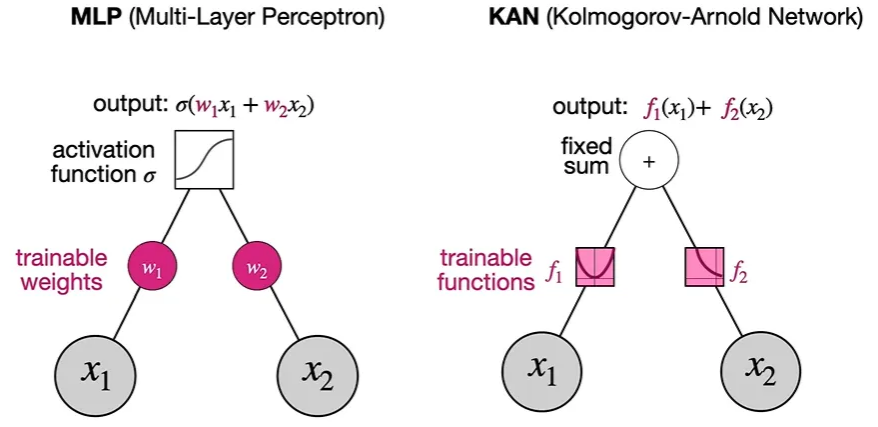
- MLP는 각 노드의 x 값에 weight를 곱해 더한 후, activation function (ex.
sigmoid)을 적용하여 output을 낸다면,
이때 각 weight는 최적의 값을 찾기 위한 train하는 대상이 된다. - KAN의 경우, 각 x값을 activation function을 적용한 후, 더하게 된다. 이때 각 값을 더할 때 적용되는 weight 값은 1이다. ( )
이때는 각 input값에 적용되는 activation function(, )이 train하는 대상이 된다.
이제 각 Nueral Network(NN) 을 train하는 방식에 대해 좀 더 살펴보도록 하겠다.
-
MLP
먼저 일반적인 NN인 MLP의 경우,

Loss function의 가장 최저점, loss가 최소가 되는 지점일 때의 weight를 찾는 것이 목표가 된다.
- 처음에는 random한 weight으로 시작한다.
예를 들어 w1=0, w2=0으로 시작할 수 있다. → 그래프에서 high loss 인 지점이 된다. - 그래서 gradient descent를 이용해서 계속해서 weight를 바꾸게 된다.
- loss function의 값이 최소가 되는 지점에 오게 되면, 그 때의 weight 값이 최적의 weight 값으로 결정되게 된다.
-
KAN
다음으로 KAN의 경우,
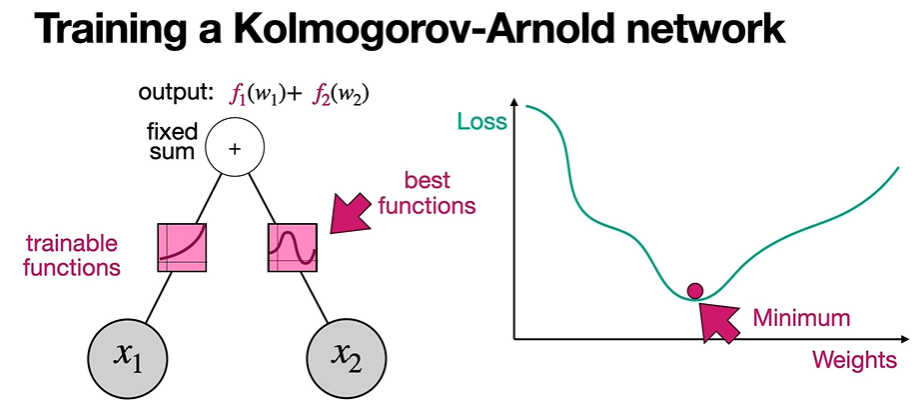
마찬가지로 초반의 random한 function을 시작으로, descend함에 따라 activation function이 변화하는데, 이때 loss가 가장 최저가 되게 하는 activation function을 찾아내는 것이 train 과정이 되겠다.
이때 문제점은,
과연 ‘function’을 어떻게 train할 것이냐, 이다.
weight은 train하는 것이 상상이 가능하다. 그러나, function의 경우 파라미터가 너무 많다.
그래서 솔루션은,
모든 function들을 사용하는 것이 아니라, function들을 단순화하는 것이다.
즉, function을 적은 수의 파라미터를 가지도록 나타내고 그 파라미터를 train하는 것이다.
B-Splines
더 적은 파라미터를 갖는 함수로 변형하는 아이디어는 다음과 같다.
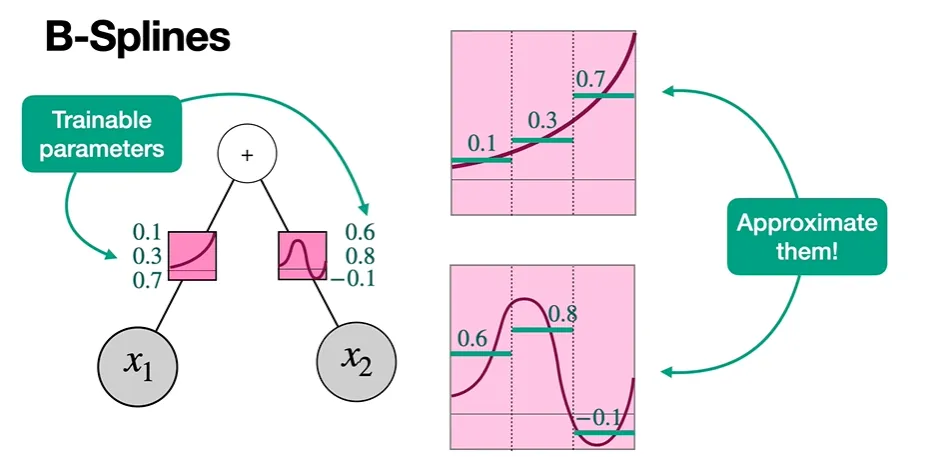
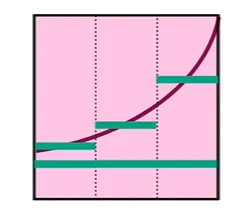
예를 들어 위 노드를 갖는 NN의 최적의 활성화 함수가 위와 같다(왼쪽 트리의 핑크색 박스)고 하자.
이때 각 활성화 함수를 갖고 와서 세등분으로 쪼갠 후, 각 등분한 함수 부분을 가장 단순한 방식(가로직선 형태의 상수 함수)로 approximate할 수 있다.
위쪽 함수의 경우, 0.1, 0.3, 0.7 값을 갖는 상수 함수로 approximate되며,
아래쪽 함수의 경우, 0.6, 0.8, -0.1 형태의 상수 함수로 approximate할 수 있다.
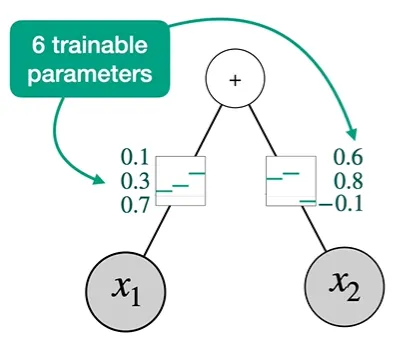
이렇게 각 함수로부터 trainable한 파라미터를 뽑아낼 수 있게 된다.
이로써 우리는 6개의 parameter를 가진 Nueral Network를 train할 수 있게 된다.
이제, B-spline이 무엇인지 살펴보겠다.
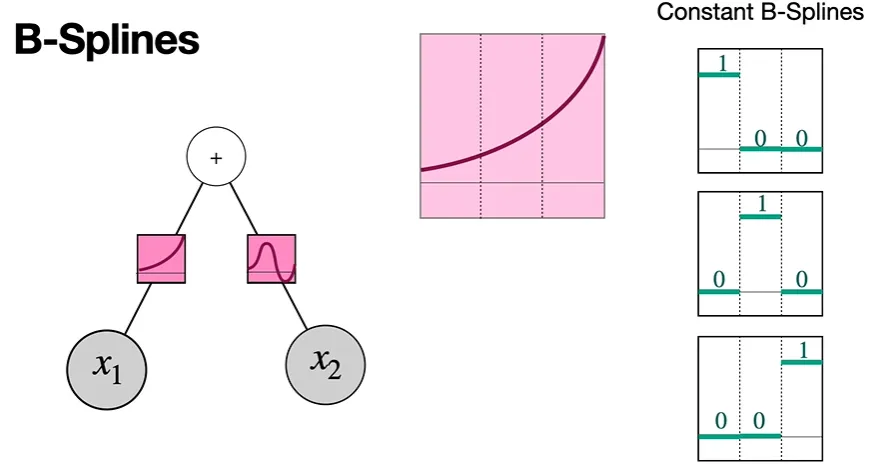
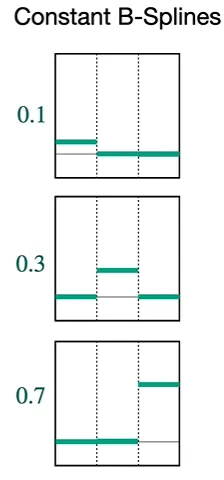
우리가 활성화 함수를 세등분으로 쪼갠다고 했을 때, 첫번째 그림의 맨 오른쪽과 같은세 개의 constant B-Spline(상수함수 B-Spline)들을 생각할 수 있다.
이때, 우리가 0.1, 0.3, 0.7 파라미터 값을 세 개의 constant 그래프에 각각 곱하게 되면,
두번째 그림과 같이 높이가 1인 부분이 변화하는 것을 볼 수 있다. 높이가 0인 부분은 그대로 0이다.
이제, 세 개의 그래프를 더하게 되면,
 위와 같이 우리가 approximate하고자 했던 기존 활성화함수의 approximate한 형태가 나타남을 알 수 있다. (0은 더해도 영향x)
위와 같이 우리가 approximate하고자 했던 기존 활성화함수의 approximate한 형태가 나타남을 알 수 있다. (0은 더해도 영향x)
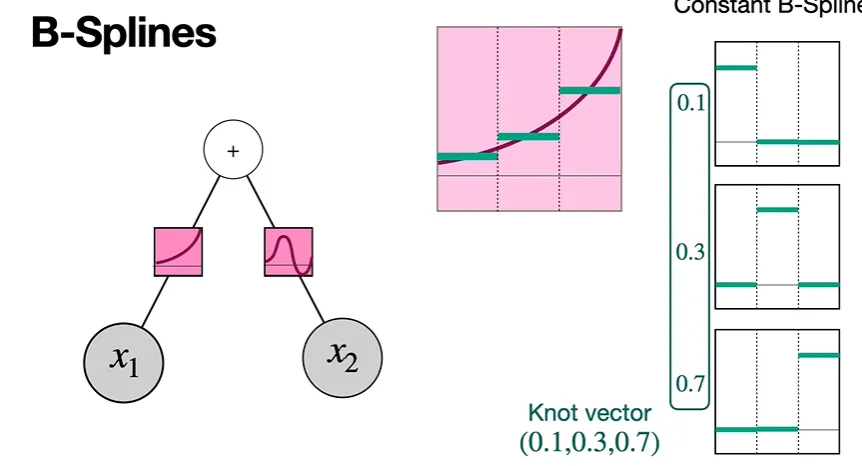
이때 0.1, 0.3, 0.7의 각 숙자를 Knot vector라고 한다.
두번째 활성화 함수도 마찬가지로,
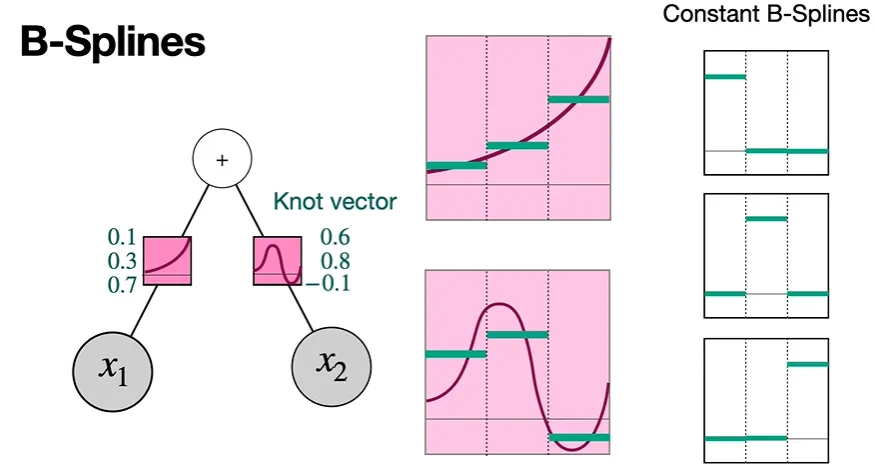 0.6, 0.8, -0.1이 이 활성화 함수의 knot vector가 된다.
0.6, 0.8, -0.1이 이 활성화 함수의 knot vector가 된다.
각 활성화 함수를 최대한 잘 단순화한 것을 알 수 있다.
물론, 우리는 더 나은 B-splines를 활용해 더 나은 approximation을 할 수도 있다.
더 많은 숫자, 더 크기가 큰 knot vector가 될 수 있겠지만, 우리는 더 원래 활성화 함수에 가깝게 만들 수 있다.
Linear B-Splines
다음은 또 다른 형태의 B-Spline이다.
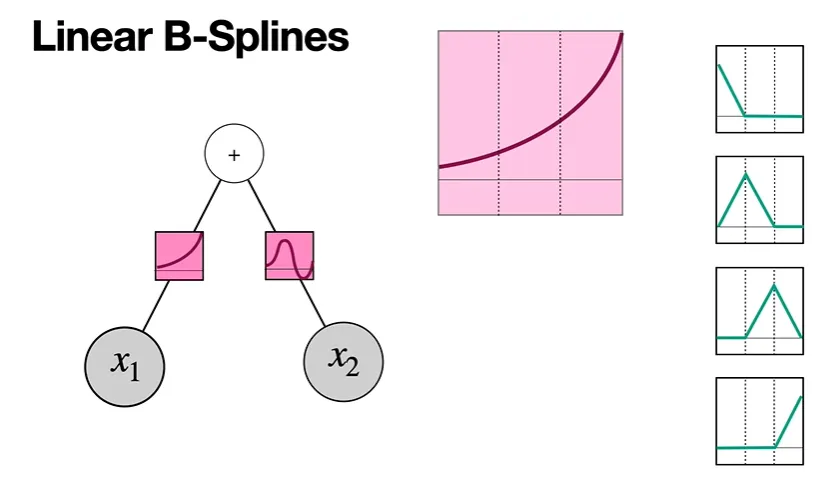
맨 오른쪽과 같이 linear한 함수로 이루어진 B-Spline들임을 알 수 있다.
이때 정점의 높이는 상관이 없다고 한다.
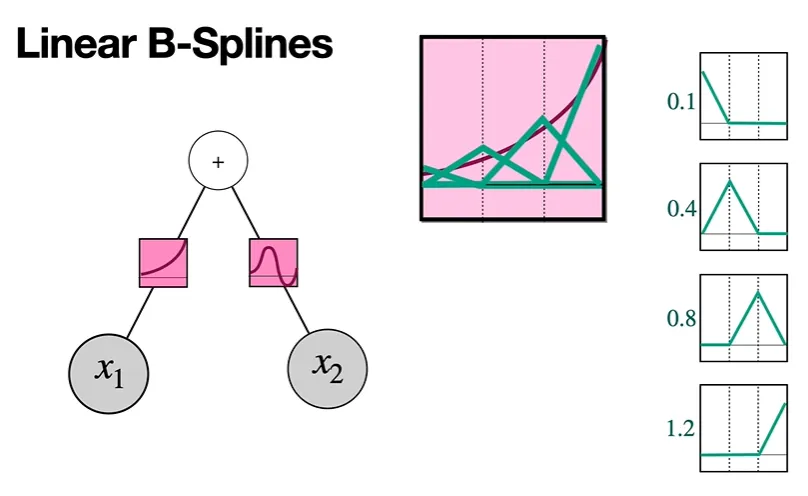
각 B-Spline에 숫자를 곱하고, 구한 그래프를 위와 같이 모두 더한다.
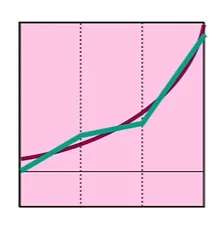
그러면 다음과 같이 활성화 함수와 훨씬 더 유사하게 approximation된 것을 확인할 수 있다.
두번째 활성화 함수에 대해서도 마찬가지로 다음과 같이 approximate할 수 있겠다.
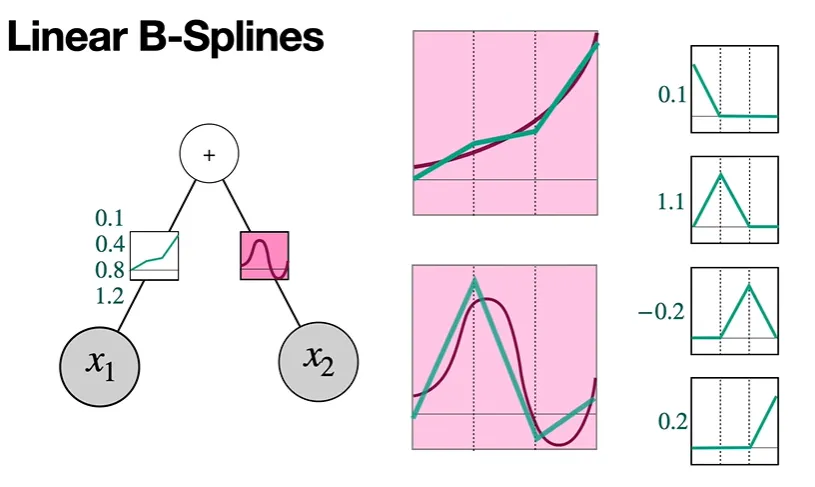 그리고 0.1, 1.1, -0.2, 0.2와 같은 knot vector를 얻을 수 있다.
그리고 0.1, 1.1, -0.2, 0.2와 같은 knot vector를 얻을 수 있다.
Quadratic B-Splines
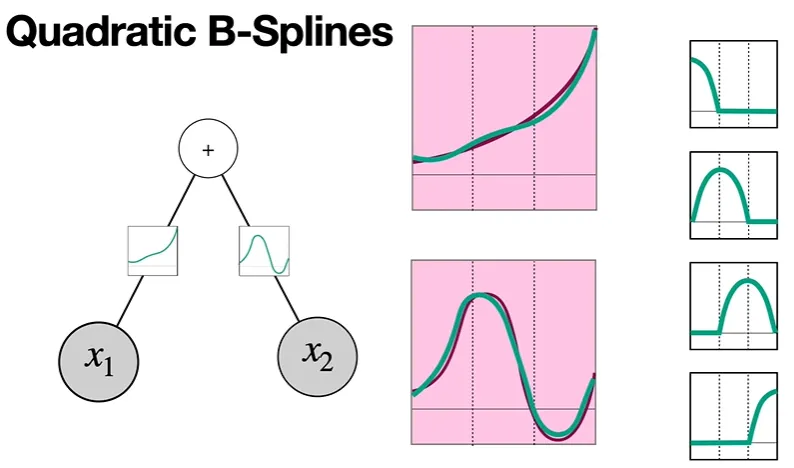 더욱 activation function과 유사한 것을 볼 수 있다.
더욱 activation function과 유사한 것을 볼 수 있다.
More B-Splines
위에서는 활성화 함수를 쪼갤 때, 세등분을 하였지만 만약 더 큰 수로 등분하여 쪼갠다면,
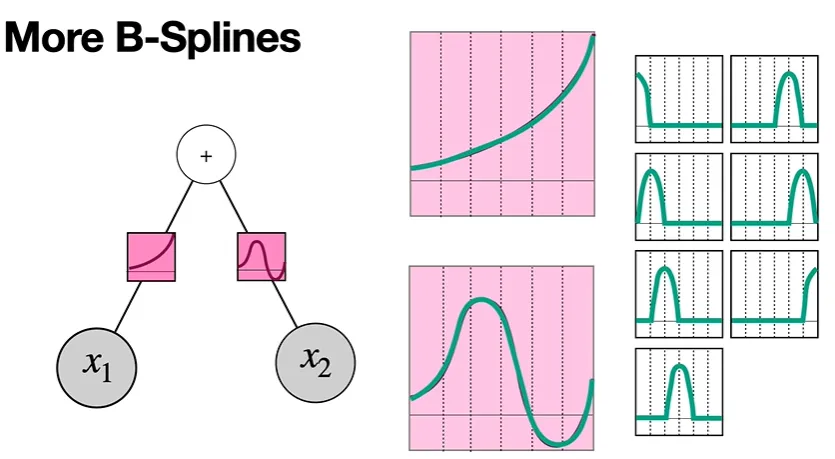
예를 들어 7등분을 하고, 더 많은 수의 spline을 이용한다면, approximation은 더욱더욱더욱더 activation function과 비숫해지며, 대신 Knot vector는 더 커진다 —7개의 파라미터가 생기게 된다.
따라서 spline의 수와, 어떤 종류의 spline을 쓰냐에 따라 하이퍼파라미터는
더 많게 될 수록 더 approximation이 정확해지지만 또 너무 많지는 않아야 한다—NN이 복잡해질 수 있으니까
Notation
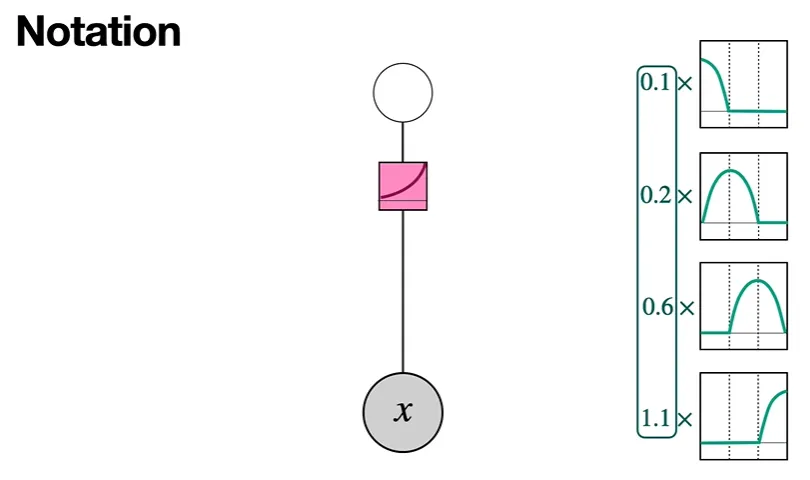 다음과 같이 Qudratic Splines를 쓴다고 하자.
다음과 같이 Qudratic Splines를 쓴다고 하자.
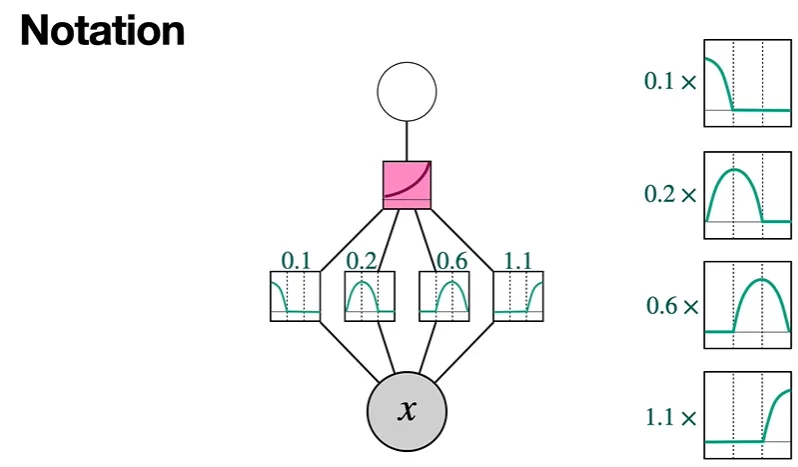 이때 각 spline을 사이에 나열하고, edge로 연결한다. 그리고 knot vector의 각 숫자를 곱한다.
각 숫자는 우리의 새로운 neural network의 weight이 될 것이다.
그렇게 함으로써 activation function을 approximation할 수 있을 것이다.
이때 각 spline을 사이에 나열하고, edge로 연결한다. 그리고 knot vector의 각 숫자를 곱한다.
각 숫자는 우리의 새로운 neural network의 weight이 될 것이다.
그렇게 함으로써 activation function을 approximation할 수 있을 것이다.
다음은 커다란 KAN이 어떻게 생겼는지 나타낸 것이다.
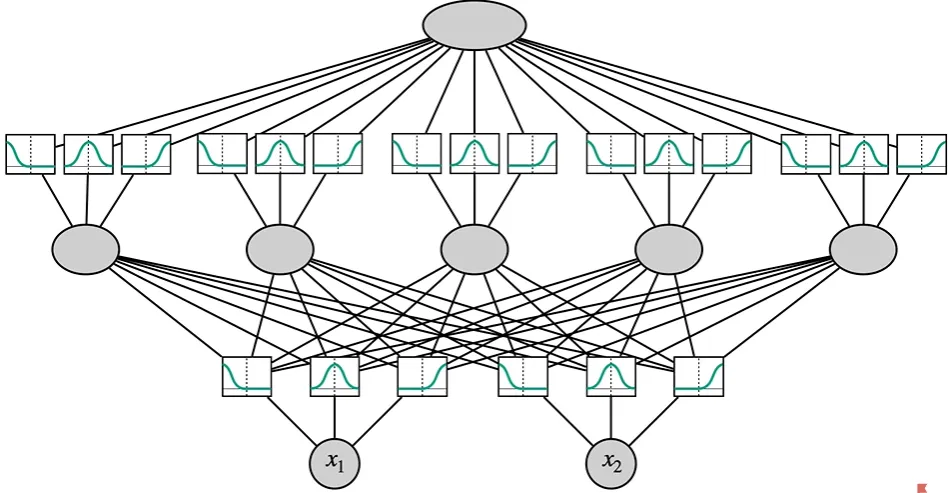
먼저, input layer가 존재하고, 각각의 node에는 splines들이 연결되어 있다.
예를 들어 3개의 spline이 연결되어 있다.
그리고 나서는 다음 layer(활성화 함수 노드로 이루어진(아래는 5개)에 연결되고,
그리고 또 다시 spline에 연결, 그리고 이후 하나의 output layer에 연결된다.
각 weight(knot vector들)은 gradient descent로 train된다.
다음은 Kolmogorov-Arnold Theorem의 수식이다.

새로운 AI는 이를 기반으로 모든 것이 쌓여나간다.
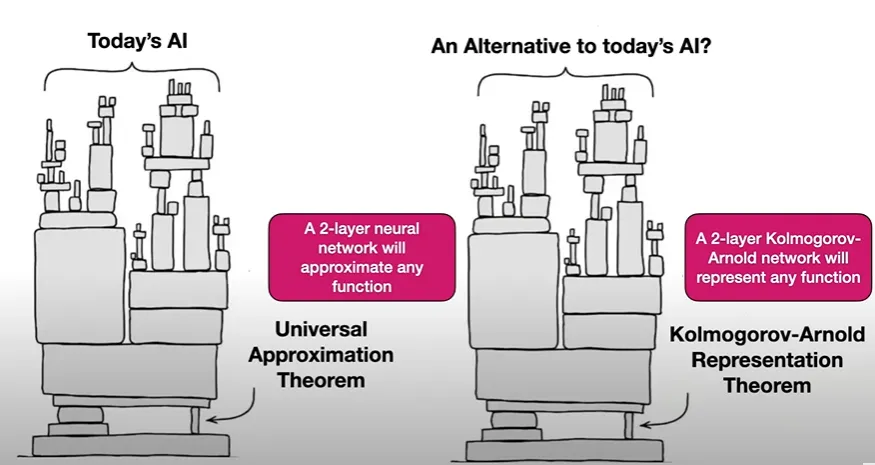
전체적인 모습:
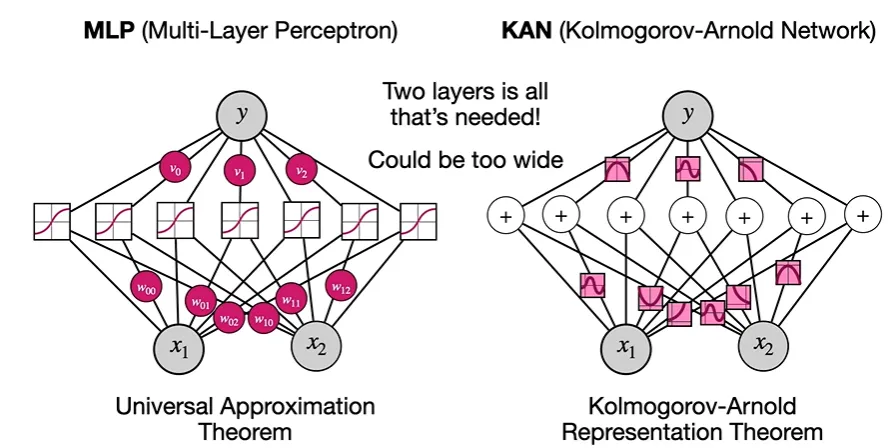
오직 두 개의 layer만으로 충분하다.
각각의 수학적인 함수들을 어떻게 표현할 것인가:
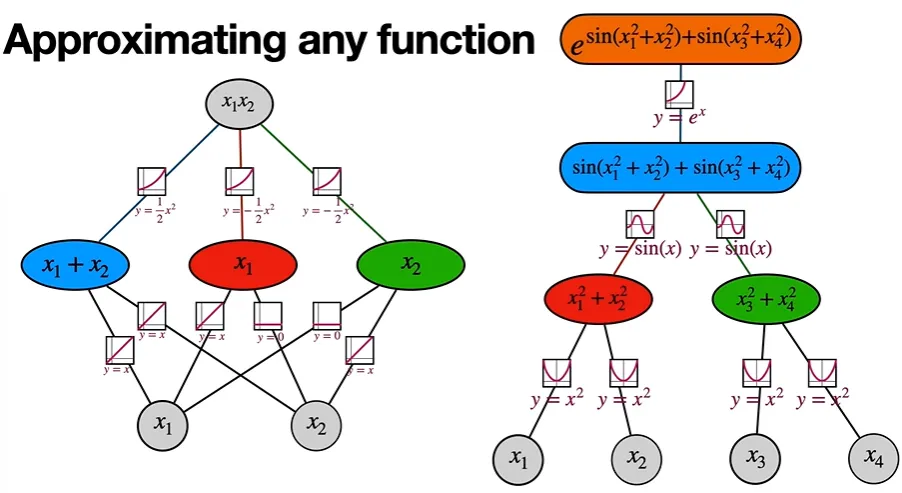
Kolmogrov-Arnold Theorem
어떤 함수가 더 단순한가?