1. Preliminary : 벡터 외적

3차원 공간 상의 두 벡터 $\vec a$ , $\vec b$가 만드는 외적 $\vec a \times \vec b$ 의 크기는 두 벡터가 만드는 평행사변형의 면적과 같고, 그 방향은 평행사변형에 수직인 방향이다.

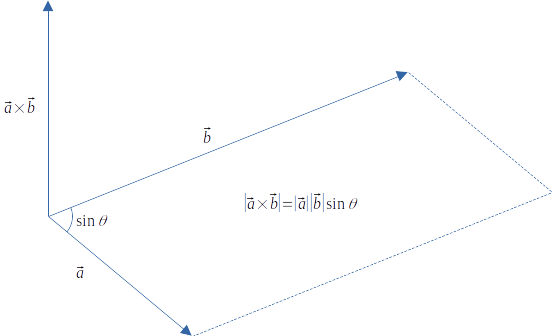
방향

외적의 방향은 전자기장의 오른손 법칙을 따른다고 한다. 근데 난 문과라 전자기장 같은 건 모르겠고 이 영상을 보도록 하자.

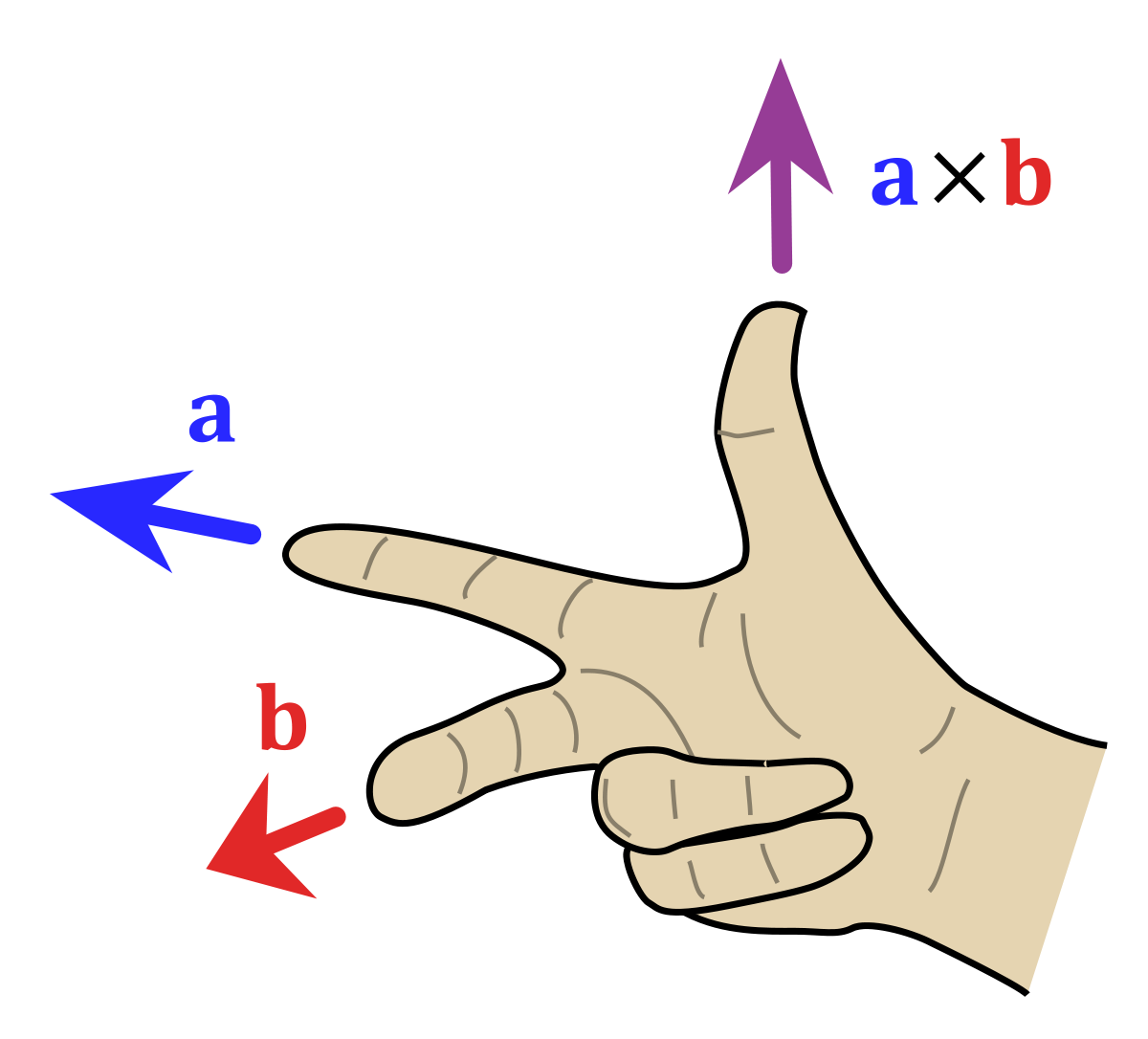
벡터 $\vec a$에서 벡터 $\vec b$ 로 반시계 방향으로 이동한다면 벡터 외적의 방향은 위가 되고, 반대의 경우 아래가 된다.

계산

성질

• 교환 법칙이 성립하지 않음 : 두 벡터를 서로 교환하면 크기는 같지만 방향이 반대가 됨
• 결합 법칙이 성립합지 않음
• 분배 법칙이 성립

2. CCW 알고리즘

벡터 외적을 이용해 평면 상 세 점의 방향성을 파악하는 데에 사용한다.

아래와 같이 점 a, b, c, 주어지고 a, b, c,의 순서대로 세 점의 방향성을 파악하려 한다고 하자

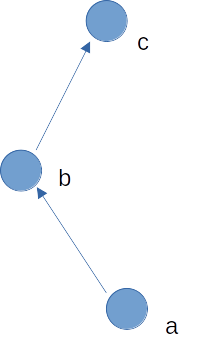
$\vec{ab}, \vec{bc}$의 벡터를 만들고 외적을 구해보자. 앞서 외적이 3차원 공간에서 논의된 것과 달리, 지금은 2차원 평면 위의 점의 방향성을 찾으니 z를 0으로 두고 구하면 된다.

앞서 논의된 외적의 방향에 따라 $x_1y_2 + x_2y_3+x_3y_1 - (y_1x_2 + y_2x_3 + y_3x_1)$ 이 음수이면 점 a, b, c는 시계, 0이면 일직선 상, 양수이면 반시계의 방향성을 가진다.

코드

typedef pair<int, int> Point; //first = x좌표, second = y좌표라 하자

int ccw(Point p1, Point p2, Point p3){
	int ret = p1.first * p2.second + p2.first * p3.second + p3.first * p1.second)
		- (p2.first * p1.second + p3.first * p2.second + p1.first * p3.second);
	if (ret < 0) return -1;
	if (ret > 0) return 1;
	return 0;
}

관련 문제 : 골드 5 CCW