1. 선분 교차 판정

CCW를 이용해 풀 수 있는 대표적인 문제에는 두 선분의 교차 판정이 있다.

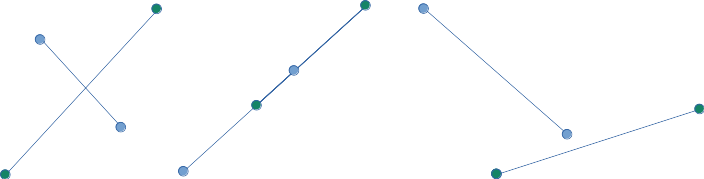
첫 번째, 두 번째는 선분들이 서로 교차하는 케이스고 세 번째는 교차하지 않는 케이스다.

2. CCW를 이용한 교차 판정

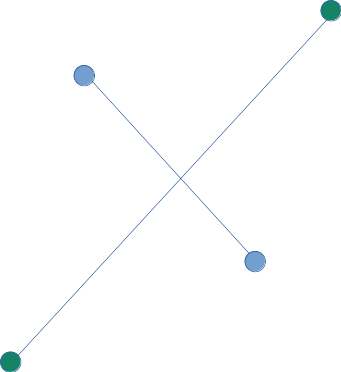
첫 번째 케이스를 초록색 두 끝점을 이은 선분을 기준으로 보자. 나머지 두 파란 점들은 선분을 기준으로 양쪽으로 나뉠 수 있다.

CCW를 이용해서 살펴보자.

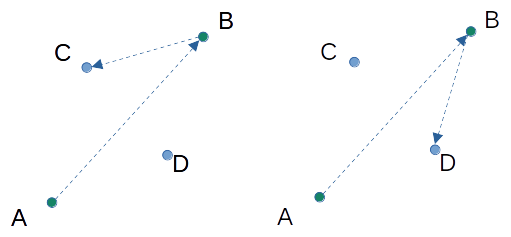
점 A, B, C는 순서대로 반시계 방향을 이루고, A, B, D는 순서대로 시계 방향을 이룬다. [[CCW]]에서 나온 코드를 이용한다면 ccw(A, B, C) == 1, ccw(A, B, D) == -1이고, ccw(A, B, C) * ccw(A, B, D) == -1이 된다.

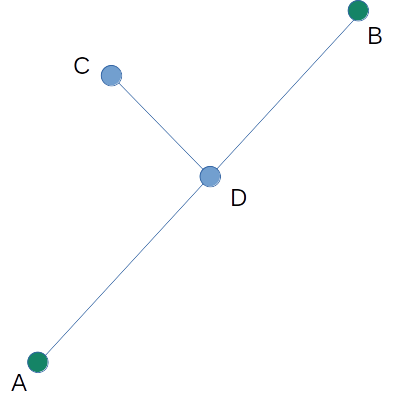
하지만 위와 같이 점 하나가 점 A, B가 이루는 선분 위에 올라가는 경우도 있을 수 있다. 점 A, B, D가 일직선을 이루므로 ccw(A, B, D) == 0이 된다. 이 경우 ccw(A, B, C) * ccw(A, B, D) == 0이 된다.

따라서 선분 AB, CD가 서로 교차하려면 ccw(A, B, C) * ccw(A, B, D) <= 0이 되어야 한다. 하지만 이 조건을 만족한다고 해서 반드시 선분 AB, CD가 서로 교차하는 것은 아닌데 다음의 케이스가 있기 때문이다.

예외 케이스 (1)

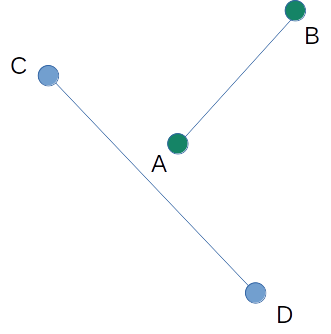
이와 같은 케이스에서ccw(A, B, C) * ccw(A, B, D) <= 0은 만족되지만, 선분 AB, CD는 서로 교차하지 않는다. 이런 케이스를 제외하기 위해서는 선분 CD를 기준으로 점 A, B가 서로 다른 곳에 있는지 확인해봐야 한다. 만약 두 선분이 서로 교차한다면 ccw(C, D, B) * ccw(C, D, A) <= 0이 만족된다.

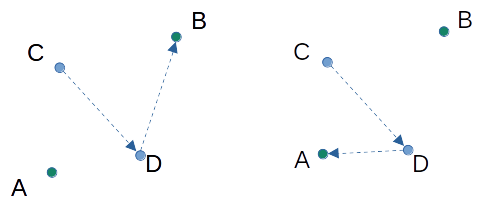
한편 아래와 같이 두 선분이 서로 교차하지 않는 경우에는 ccw(C, D, B) * ccw(C, D, A) > 0이 되어 조건을 만족하지 않음을 확인할 수 있다.

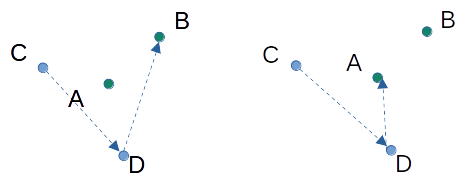
따라서 두 선분 AB, CD가 서로 교차하기 위해서는 다음의 조건을 만족해야한다.
ccw(A, B, C) * ccw(A, B, D) <= 0 && ccw(C, D, A) * ccw(C, D, B) <= 0

예외 케이스 (2)

하지만 위 조건에도 예외 케이스가 있는데 다음과 같이 두 선분이 일직선 위에 있는 경우다.

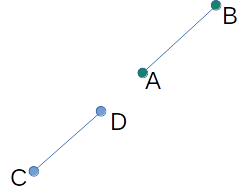
이 경우에 ccw(A, B, C) * ccw(A, B, D) == 0 && ccw(C, D, A) * ccw(C, D, B) == 0이 되어 위 조건은 만족되지만 두 선분은 서로 교차하지 않는다. 그렇다면 두 선분이 일직선 위에 있으면서 서로 교차하는 경우에는 어떤 게 있을까?

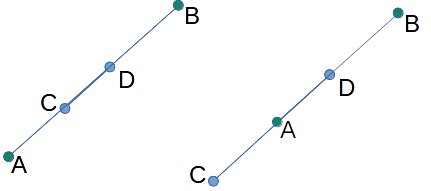
두 선분이 일직선 위에 있으면서 서로 교차하는 경우는 위와 같이 한 선분의 끝점 하나 이상이 다른 선분에 포함되는 경우다. 이는 다음과 같이 확인할 수 있다.

1) 두 선분을 끝점을 각각 x, y좌표 순으로 정렬한다.
2) 한 선분의 큰 끝점이 다른 선분의 작은 끝점보다 크거나 같은지 확인한다.
- 즉 A < B, C < D라 할 때, B <= C 이고 D <= A인지 확인한다.

3. Code

typedef pair<int, int> Point; //first = x좌표, second = y좌표라 하자
typedef pair<Point, Point> Segment; //선분 

int ccw(Point p1, Point p2, Point p3){
	int ret = p1.first * p2.second + p2.first * p3.second + p3.first * p1.second)
		- (p2.first * p1.second + p3.first * p2.second + p1.first * p3.second);
	if (ret < 0) return -1;
	if (ret > 0) return 1;
	return 0;
}

bool intersect(Segment seg1, Segment seg2){

	Point p1 = seg1.first, p2 = seg1.second;
	Point p3 = seg2.first, p4 = seg2.second;

	int p1p2 = ccw(p1, p2, p3) * ccw(p1, p2, p4); //조건 만족 여부
	int p3p4 = ccw(p3, p4, p1) * ccw(p3, p4, p2); //예외 케이스 1 확인

	if (p1p2 == 0 && p3p4 == 0) {
		if (p1 > p2) swap(p1, p2); //x, y축 순으로 정렬
		if (p3 > p4) swap(p3, p4);
		
		//한 선분의 큰 점이 다른 선분의 작은 점보다 큰지 확인한다. 
		return (p2 >= p3 && p4 >= p1);
	}

	return p1p2 <= 0 && p3p4 <= 0;
}
`