1. 볼록 껍질(convex hull)

직관적으로 설명하면, 평면 상의 볼록 껍질은 여러 점들의 집합이 주어졌을 때, 이 집합의 일부만을 꼭짓점으로 가지면서 모든 점들을 감싸는 볼록 다각형의 꼭짓점 집합 중 가장 작은 것을 말한다.
아래와 같은 점들이 있다고 하자.

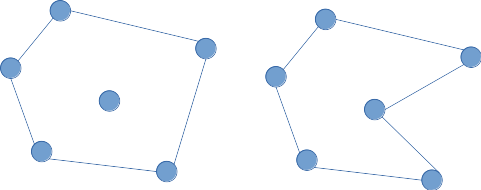
이 점들의 일부를 아래 그림의 왼쪽과 같이 이으면 볼록 껍질을 되며, 오른쪽과 같이 잇는 경우는 모든 점들을 감쌀 수는 있지만 오목 다각형이기 때문에 볼록 껍질이 아니다.

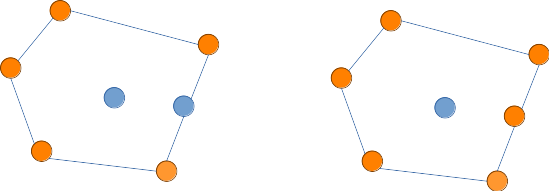
한편 아래 그림에서(제일 오른쪽에 있는 세 점이 일직선을 이룬다고 하자), 왼쪽은 볼록 껍질이지만 오른쪽은 아니다. 이 둘은 모두 주어진 모든 점들을 포함하는 볼록 다각형을 만들고는 있지만, 볼록 껍질은 그러기 위한 최소 개수의 점 집합이어야 하기 때문이다.

점들이 주어졌을 때 볼록 껍질을 찾는 대표적인 알고리즘 중 하나가 그레이엄 스캔이다.

2. 그레이엄 스캔

그레이엄 스캔은 다음의 순서로 진행한다.

1. y좌표가 가장 작은 점 P를 찾는다.
   • 이때 y 좌표가 동일한 점들이 여러 개 있으면 x좌표가 가장 작은 점을 선택한다.
   • 이 점의 경우 항상 볼록 껍질에 포함되어 있다.
2. 점 P를 기준으로 모든 점들을 x축에 대해 각도가 증가하는 순으로 정렬한다.
   • 이때 따로 각 점과 점 P가 이루는 각도를 계산할 필요는 없다.
   • CCW를 이용해 비교 함수를 만들고 점들을 반시계 방향으로 정렬함으로써 상대적인 각도만을 고려할 수도 있다.
3. 각 점에 대해, 스택의 위쪽 두 점과 이 점이 어떤 방향으로 회전하는지를 판정한다.
   • 앞의 두 점과 현재의 점이 반시계 방향이 아니라 시계 방향을 이루는 경우, 끝에서 두 번째 점(즉 스택의 가장 위에 있는 점)은 볼록 껍질 위에 있는 점이 아니라 볼록 껍질 안에 있는 점이다.
   • 만약 반시계 방향을 이룬다면 스택에 집어넣는다.
4. 3의 과정을 시작점으로 돌아올 때까지 반복한다.

그림과 함께 살펴보자.

(1) y좌표가 가장 작은 점 P 찾기

아래 그림에서 주황색으로 색칠된 점이 가장 작은 y좌표를 가지고 있다. 이 점을 P라고 하자.

(2) 점 P를 기준으로 모든 점들을 x축에 대해 각도가 증가하는 순으로 정렬한다.

앞서 말한 것과 같이 각 점과 P가 이루는 각도를 직접 계산할 필요는 없다. CCW를 이용하면 각 각도를 따로 직접 계산하지 않고도 상대적인 각도를 알 수 있기 때문이다. 다음의 예를 보자.

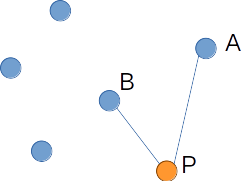
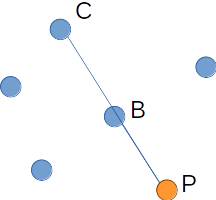
그림에서 점 A, P와 x축이 이루는 각도는 점 B, P가 x축과 이루는 각도보다 작다. 이러한 관계는 아래와 같이 점 P, A, B가 순서대로 반시계 방향을 이루는지를 확인함으로써 파악할 수 있다.

만약 B가 아래 그림과 같이 다른 곳에 위치해 있었다고 해보자.

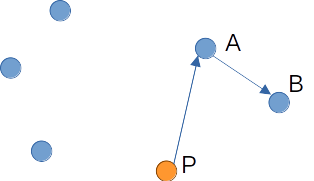
이 경우 점 A, P와 x축이 이루는 각도는 점 B, P와 x축이 이루는 각도보다 크며, 우리는 앞서와는 달리 점 P, A, B가 순서대로 시계 방향을 이루고 있음을 확인할 수 있다.

한편 아래와 같이 점 P, x축과 이루는 각도가 동일한 두 점이 있을 수도 있다. 이 경우에는 해당하는 점들과 P 사이의 거리를 기준으로 정렬한다. 그 이유는 같은 직선 위에 있는 두 점 중 점 P에 더 가까운 점은 절대 볼록 껍질에 들어가지 않기 때문이다. 이와 같은 경우, 다음의 단계에서 만약 점 P로부터 먼 점을 먼저 체크하게 된다면 볼록 껍질에 들어갔어야 할 점이 제외되는 문제가 생길 수도 있다.

정렬이 완료된 후의 결과는 다음과 같다.

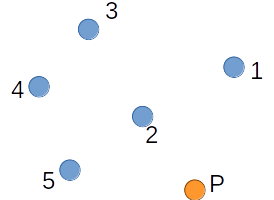
(3) 각 점에 대해, 앞의 두 점과 이 점이 어떤 방향으로 회전하는지를 판정한다.

점 P부터 시작해, 각 점에 대해 이 점이 스택에 넣은 가장 위쪽의 두 점과 어떤 방향을 이루는지를 확인한다.

점 P와 1번 점을 확인할 때에는 스택에 2개 이상의 점이 없으므로 일단 집어 넣는다.

2번 점을 스택에 넣을지를 판단하기 위해서는, 점 P, 1, 2가 반시계 방향을 이루는지를 확인해야 한다. 점 P, 1, 2가 순서대로 반시계 방향을 이루므로 점 2를 스택에 넣는다.

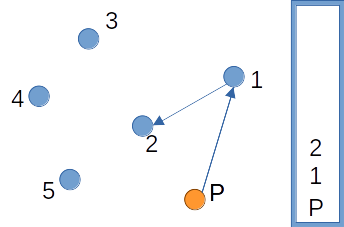
점 3의 경우에도 마찬가지로 점 1, 2, 3이 순서대로 반시계 방향을 이루는지를 확인해야 한다. 그런데 아래 그림에서 확인할 수 있듯 이 세 점은 시계 방향을 이룬다. 따라서 스택의 가장 위에 있는 점 2는 스택에서 제거된다.

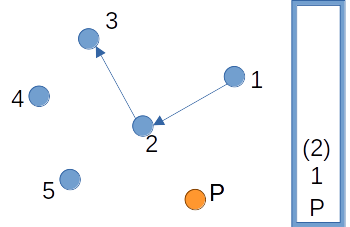
이후 3번을 스택에 넣을지는 스택에 남아있는 점 P, 1을 통해서 다시 판정한다. 점 P, 1, 3이 순서대로 반시계 방향을 이루므로 3을 스택에 넣는다.

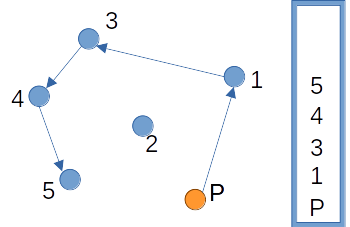
이후에도 마찬가지로 진행해 최종적으로는 다음과 같이 볼록 껍질에 속하는 점들을 모두 찾을 수 있다.

3. 시간 복잡도

그레이엄 스캔은 세 가지의 단계로 나눠져 있었다. 각 단계의 시간 복잡도는 다음과 같다.

1. 점 P 찾기. $O(N)$
   • 점들을 순회하면서 가장 작은 y축의 점을 찾는다.
2. 점 P를 기준으로 반시계 방향 정렬.
   • 정렬을 하는 데에는 $O(N\log{N})$의 시간이 걸린다
3. 스택을 이용한 각 점의 회전 방향 판정
   • 각 점에 대해, 최대 2번을 확인하므로 $O(2N) = O(N)$이다.

결론적으로 그레이엄 스캔은 $O(N\log{N})$의 시간 복잡도를 가진다.

4. 코드

typedef pair<int, int> Point;
vector<Point> vertex;
stack<int> stk;

//점 P를 찾는다.
bool compareY(Point a, Point b) {
	if (a.second == b.second) return a.first < b.first;
	else return a.second < b.second;
}

long long CCW(Point a, Point b, Point c) {
	return 1LL * (b.first - a.first) * (c.second - b.second) - 1LL * (b.second - a.second) * (c.first - b.first);
}

long long calcDist(Point a){
	return 1LL * (a.first - vertex[0].first) * (a.first - vertex[0].first) + (a.second - vertex[0].second) * (a.second - vertex[0].second);
}

bool compareAngle(Point a, Point b) {
	long long ccw = CCW(vertex[0], a, b);
	if (ccw) return ccw > 0;
	return calcDist(a) < calcDist(b);
}

int main() {
	//input 관련 처리들을 통해 vertex에 해당 점들이 입력되었다고 가정.

	//graham algorithm

	// 1단계 : 가장 y좌표가 작은 점을 찾기.(정렬하지 않는 다른 방법도 당연히 가능)
	sort(vertex.begin(), vertex.end(), compareY); //

	// 2단계 : vertex[0]은 y좌표가 가장 작은 점 P이다. 이 점 P를 제외한 다른 점들을 P를 기준으로 반시계 방향으로 정렬한다. 
	sort(vertex.begin() + 1, vertex.end(), compareAngle);

	// 3단계
	//0번째 점, 즉 점 P와 1번째 점은 비교할 점들이 없으므로 일단 스택에 집어넣는다.
	stk.push(0);
	stk.push(1);

	//2번째 점부터 본다.
	int next = 2;

	while (next < N) {
		while (stk.size() >= 2) {
			int second = stk.top();
			stk.pop();
			int first = stk.top();
			if (CCW(vertex[first], vertex[second], vertex[next]) > 0) {
				stk.push(second);
				break;
			}
		}
		stk.push(next++);
	}

	//스택의 사이즈는 볼록 껍질의 크기와 같다
	printf("%ld", stk.size());
}