지난 글에서 세그먼트의 구간 갱신이 $O(Nlog{N})$의 시간 복잡도로, 상당히 느리게 이루어짐을 봤다. 세그먼트 트리에서의 지연 전파(lazy propagation)는 이러한 문제를 해결하기 위해 쓰이는 알고리즘으로, 구간 갱신이 $O(log{N})$의 시간에 이뤄질 수 있도록 한다.

1. 아이디어

지연 전파의 기본 아이디어는 간단하다. 지금은 딱 필요한 구간까지만 갱신을 하고, 그 아래의 부분 공간들은 나중에 필요할 때까지 갱신을 미뤄두는 것이다.

세그먼트 트리로 구간합을 관리하려 할 때, 지연 전파를 사용하는 경우와 그렇지 않은 경우를 비교해보자.

지난 글에서와 마찬가지로 길이 11의 배열이 주어지고, 이를 세그먼트 트리로 관리한다 해보자.

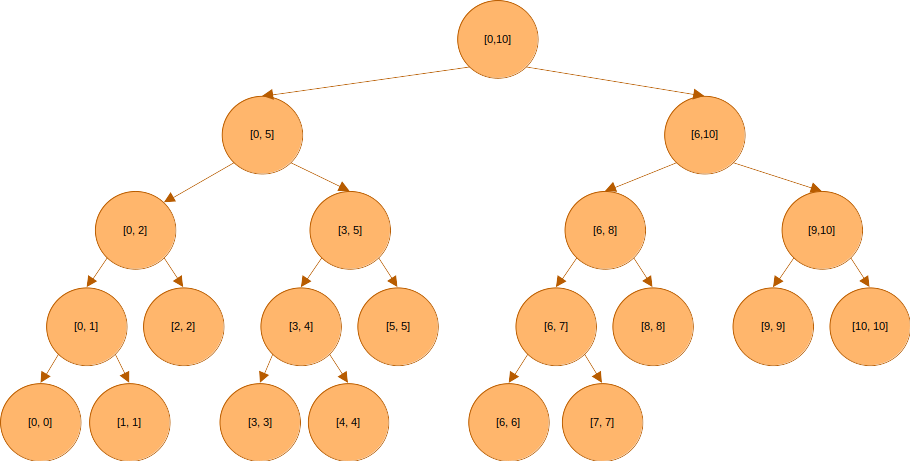
지연 전파를 사용하지 않는 경우

일단은 지연 전파를 사용하지 않고, 지난 글에서 구현했던 구간 갱신 함수를 그대로 사용해보자.

void update(int idx, int start, int end, int left, int right, int val) {
	if (right < start || end < left) return;

	if (start == end) {
		segtree[idx] += val;
		return;	
	}
	
	int mid = (start + end) / 2;

	update(idx * 2, start, mid, left, right, val);	
	update(idx * 2 + 1, mid + 1, end, left, right, val);	

	segtree[idx] = segtree[idx * 2] + segtree[idx * 2 + 1];
}

여기서 $[0, 8]$ 구간의 모든 원소에 특정값을 더하려 한다고 해보자. 위 구현을 따르면 아래에 색칠된 노드들의 값이 모두 바뀌어야 한다.

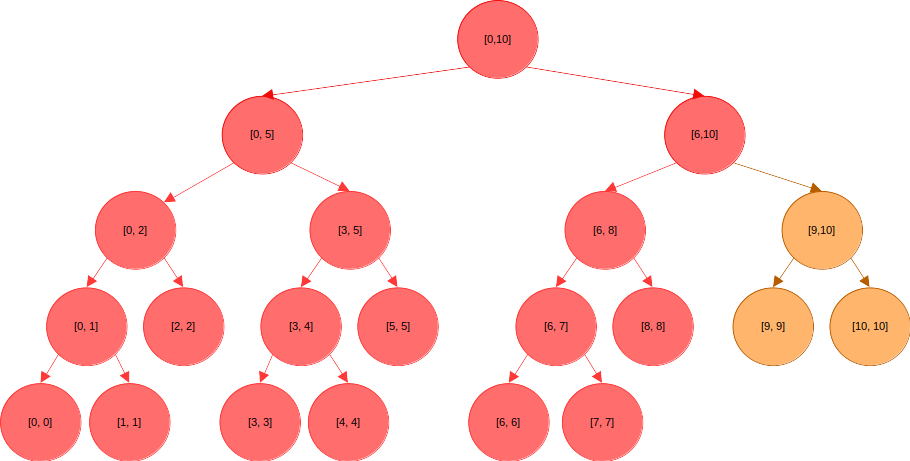
지연 전파를 사용하는 경우

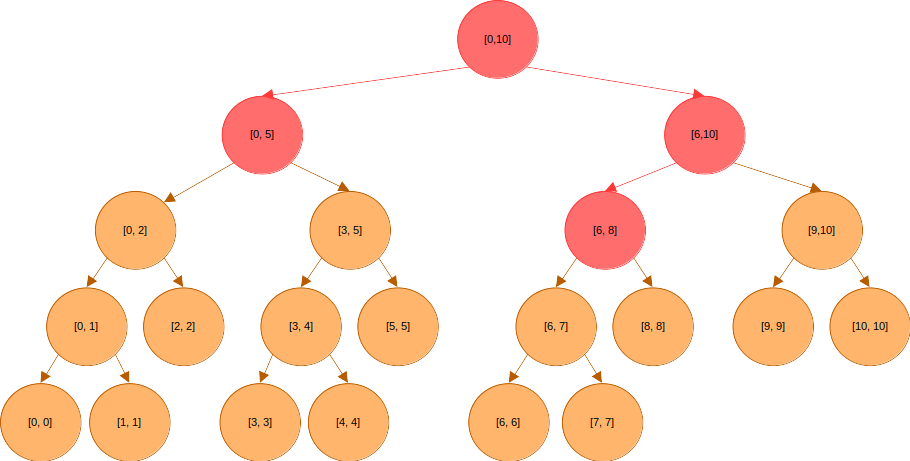
이와 달리 지연 전파를 사용해, 지금 당장 값이 바뀔 필요가 있는 부분들만 변경하고 그 외의 것들에 대한 갱신은 잠시 미뤄보자. 위와 같이 4개의 노드 값만 바뀌게 된다. 지연 전파를 사용하지 않았을 때 18개의 노드의 값이 바뀌어야 했던 것과 비교하면 확실히 빠르다.

2. 변경 사항 관리

여기서 $[4, 4]$에 대한 쿼리가 들어오면 어떻게 될까? 지금은 지연 전파를 사용하고 있기 때문에 $[0, 5]$ 노드까지는 값이 변했지만 그 아래의 $[3, 5], [3, 4], [4, 4]$의 값은 변하지 않았다. 이제는 $[3, 5], [3,4], [4,4]$ 구간까지 변경 사항을 반영시켜야 한다.

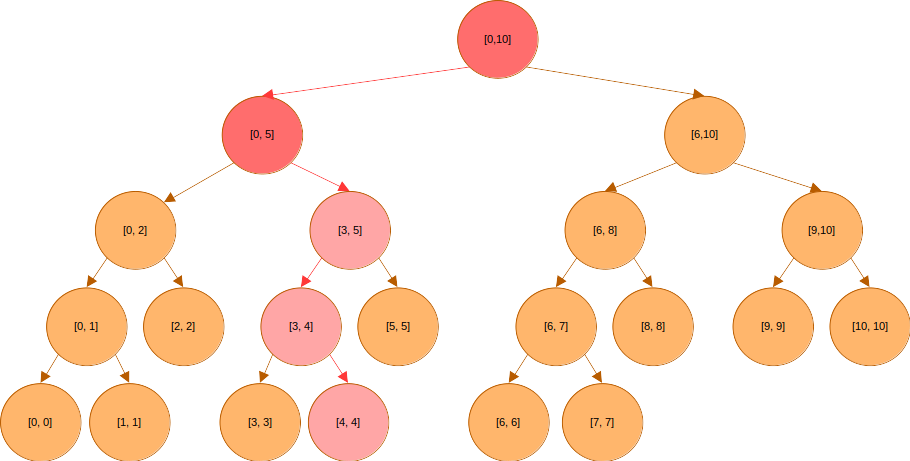
이를 위해서는 미반영된 변경 사항을 관리하기 위한 자료 구조가 추가로 필요하다. 아래와 같은 세그먼트 트리의 파란색 원(lazy라 하자)이 해당 구간에 미반영된 값을 반영시키기 위해 쓰이는 자료 구조다.

미반영된 값의 반영

미반영된 값을 반영시킨다는 것은 다음과 같은 작업을 한다는 것이다.

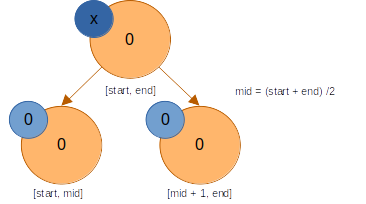
$[start, end]$ 노드에 미반영 된 값 $x$가 있다고 하자. 탐색 중 $[start, end]$ 노드를 만나면 해당 노드의 값을 $x$에 따라 바꿔준다.

구간합 세그먼트 트리라면, 이 $x$는 구간의 모든 각 원소들에 더해줄 값을 말한다. 구간 내 모든 원소에 $x$를 더해주니, 해당 구간에는 $(end - start + 1) \times x$를 더해주게 될 것이다.

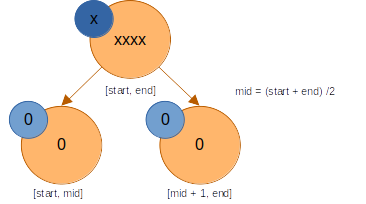
이제 바로 아래의 자식 노드들의 lazy 값을 적절히 바꿔준다. 이 값은 나중에 해당 노드들을 갱신해야 할 때 쓰이게 된다.

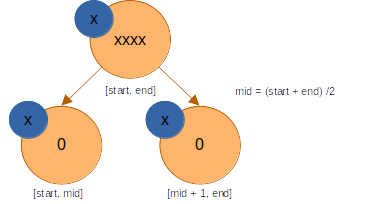
$[start, end]$ 노드의 lazy값은 반영되었으니 초기값으로 되돌려준다.

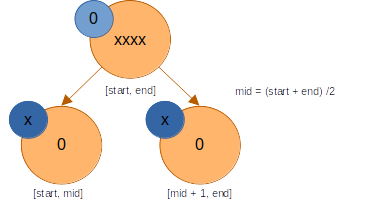
이제 다음과 같이 구간합을 관리하는 세그먼트 트리를 살펴보자.

업데이트

1. 아직 미반영된 값이 있으면 반영한다.
2. 갱신 구간에 포함되는 노드를 발견하면, 해당 노드의 lazy 값을 변경하고 반영한다.

이 트리의 $[0, 8]$ 구간의 모든 원소에 3을 더하려 한다고 해보자.

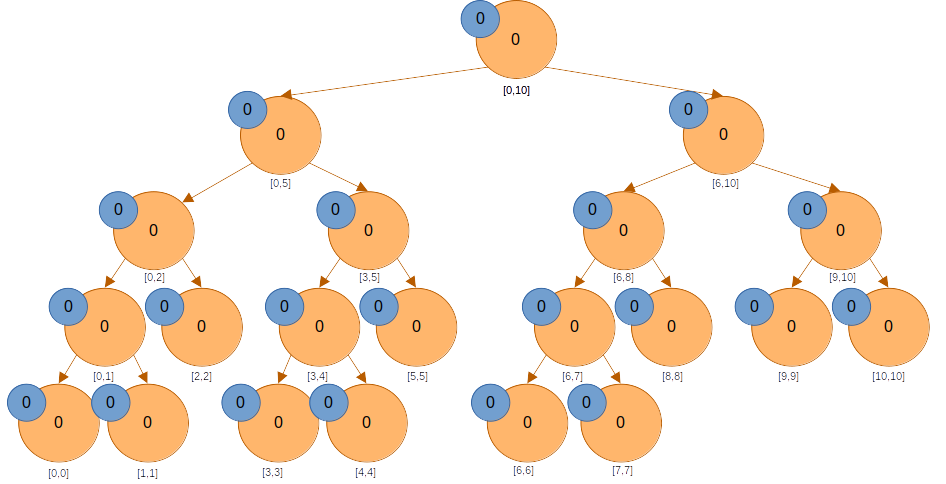
루트에서부터 시작해 내려가면서 해당 노드에 아직 반영되지 않은 값이 있으면 반영시켜준다.

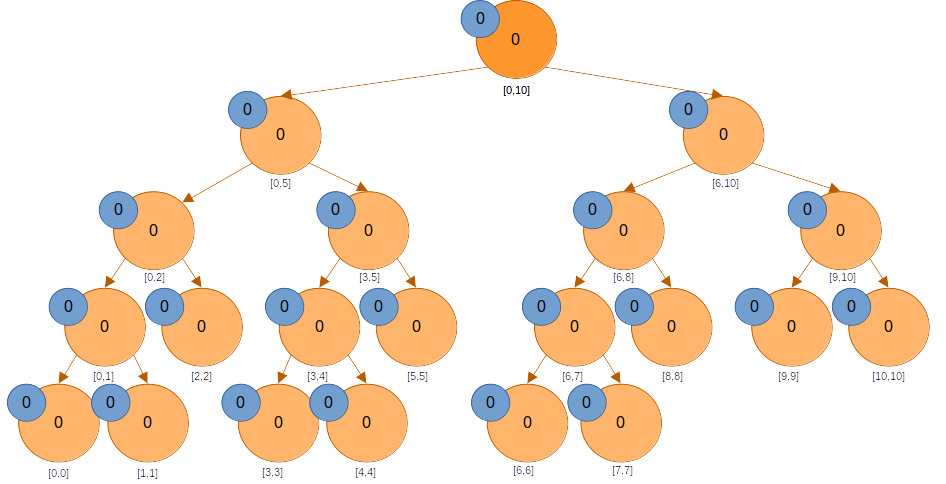
$[0, 10]$ 노드에는 아직 반영되지 않은 값이 없다. 아래로 내려가보자.

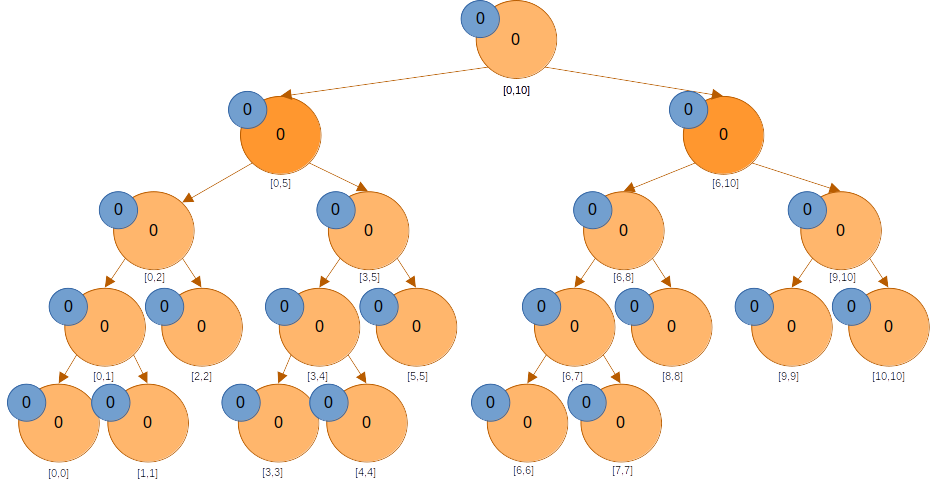
$[0, 5]$에는 미반영된 값이 없다. 하지만 $[0,5]$는 $[0,8]$에 완전히 포함되어 있는 구간이다. 해당 노드의 lazy 값에 3을 더해준다.

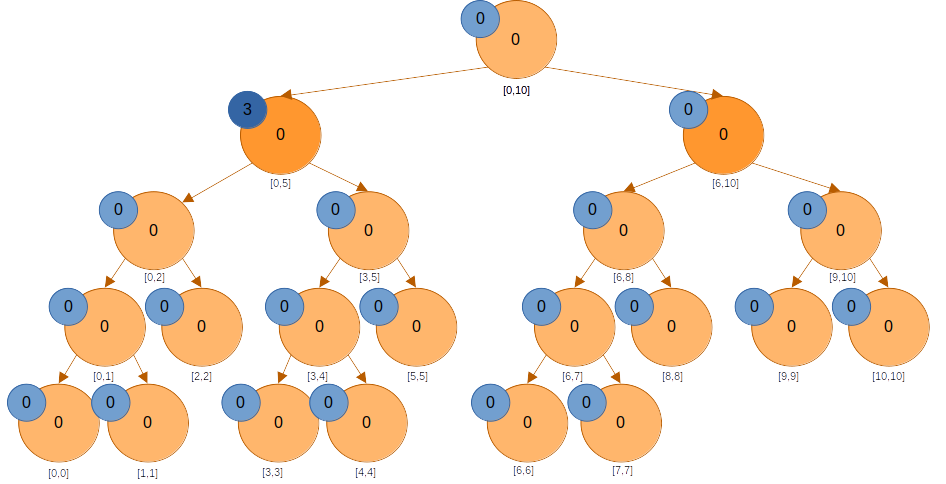
$[0,5]$의 세그트리 노드에 변화를 반영시켜준다. 구간합이므로 해당 구간에는 $(5-0+1) \times 3 = 18$이 더해진다. 값을 반영해줬으니 lazy는 0으로 바꿔 준다. 리프노드가 아니므로 두 자식의 lazy에도 변경 사항을 전파한다.

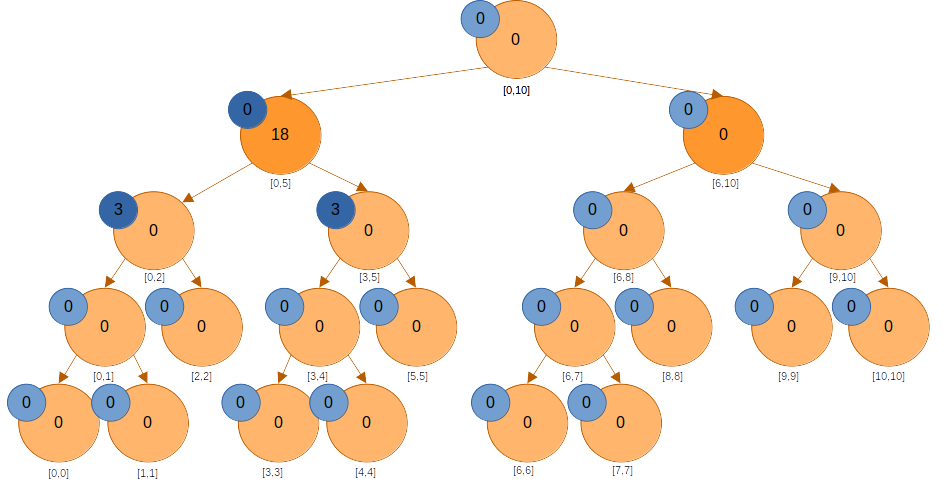
$[6, 10]$은 $[0,8]$에 포함되지 않고, 아직 미반영된 값도 없다. 아래로 내려간다.

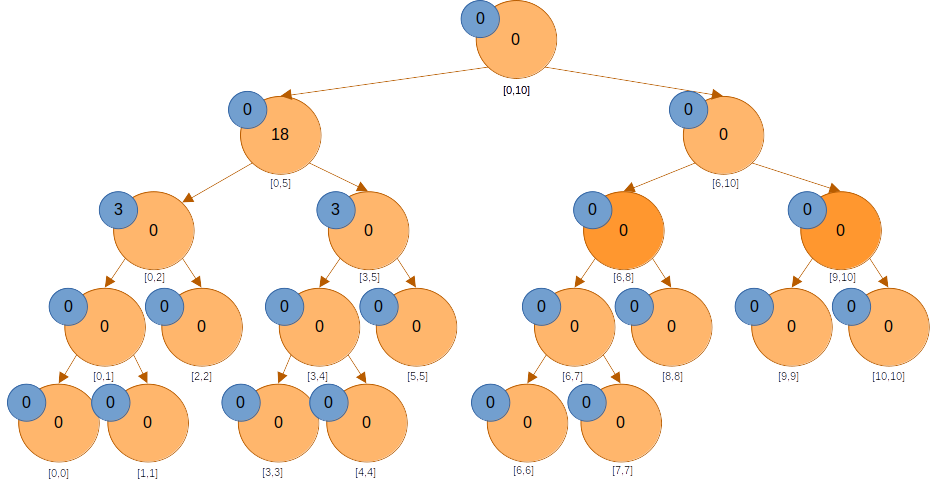
$[6, 8]$은 미반영된 값이 없지만 $[0, 8]$ 구간에 포함되어 있다. 따라서 lazy 값을 변경하고 노드의 값을 변경시킨 후 자식 노드의 lazy에도 변경할 값을 전파한다. $[6,8]$구간이므로 노드의 값에는 $(8 - 6 + 1) \times 3 = 9$가 더해진다.

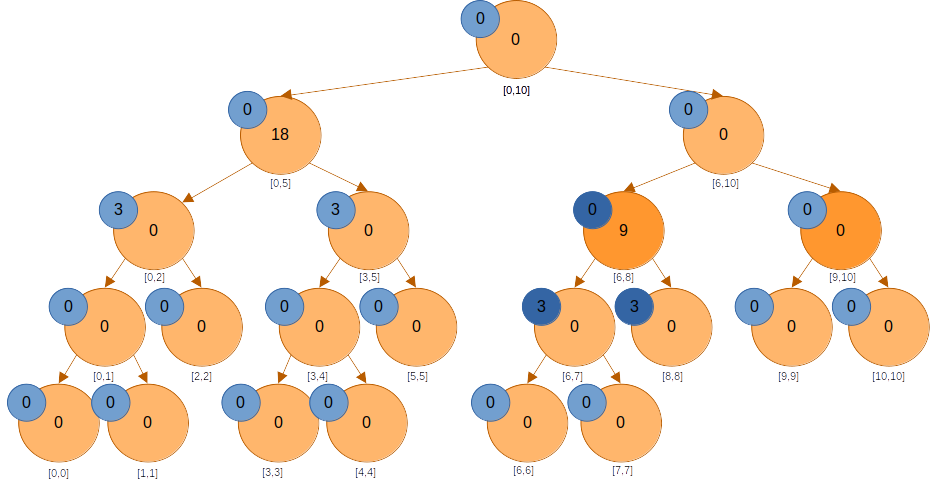
$[6, 10]$ 노드의 값은 두 자식 노드의 합으로 변한다.

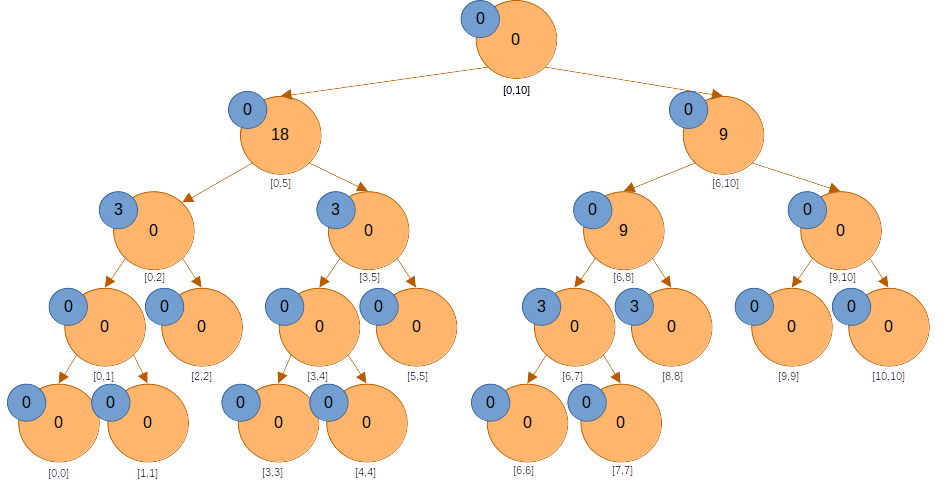
$[0, 10]$ 노드의 값도 두 자식 노드의 합으로 변한다.

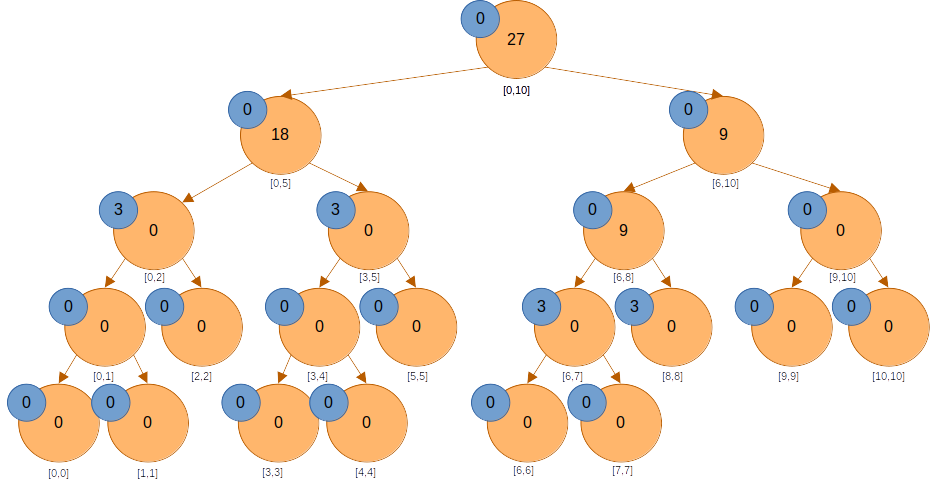
아래의 짙게 색칠된 노드들만을 변경하면서 $[0,8]$의 구간합을 업데이트했다.

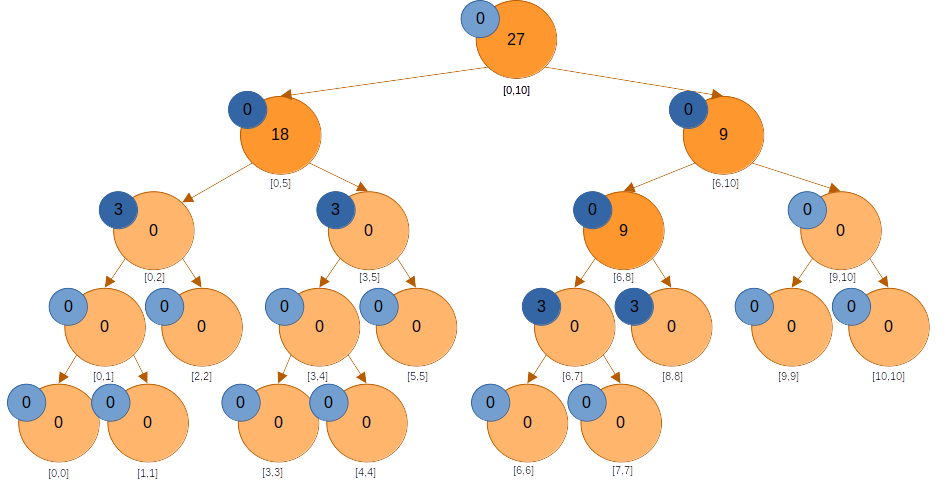
쿼리

1. 아직 미반영된 값이 있으면 반영시킨다.
2. 쿼리 구간에 포함되는 노드라면, 해당 노드의 값을 반환한다.

여기서 $[4,4]$에 대한 쿼리가 들어왔다고 하자. 앞서 $[0, 8]$ 구간의 모든 원소들에 3을 더해줬으므로 3이라는 결과가 나와야 할 것이다.

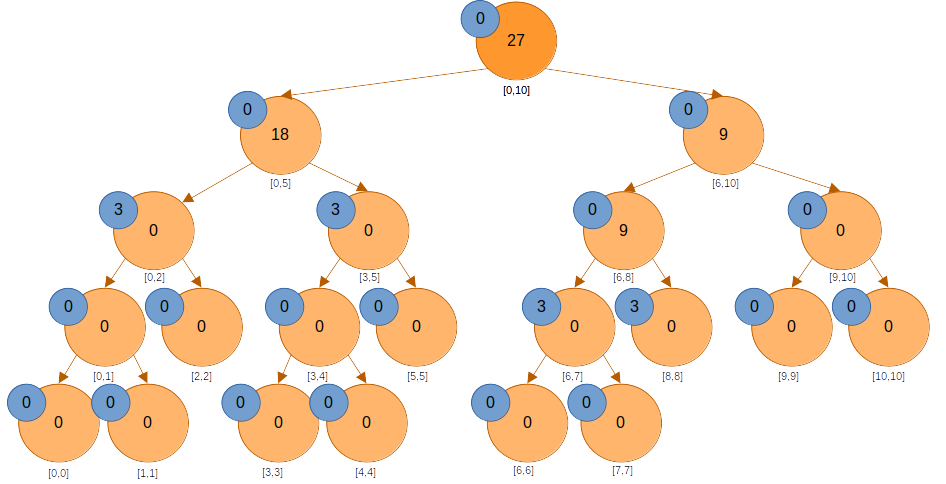
$[0, 10]$에는 미반영된 값이 없다. 내려간다.

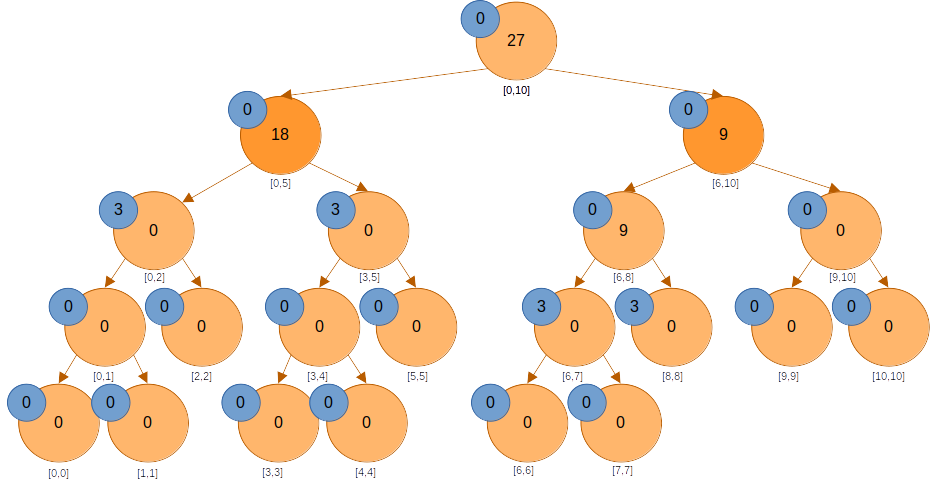
$[0, 5], [6, 10]$에도 미반영된 값이 없다. $[6, 10]$은 쿼리 구간과 겹치지 않으니 바로 0을 반환한다. $[0, 5]$ 아래로 내려간다.

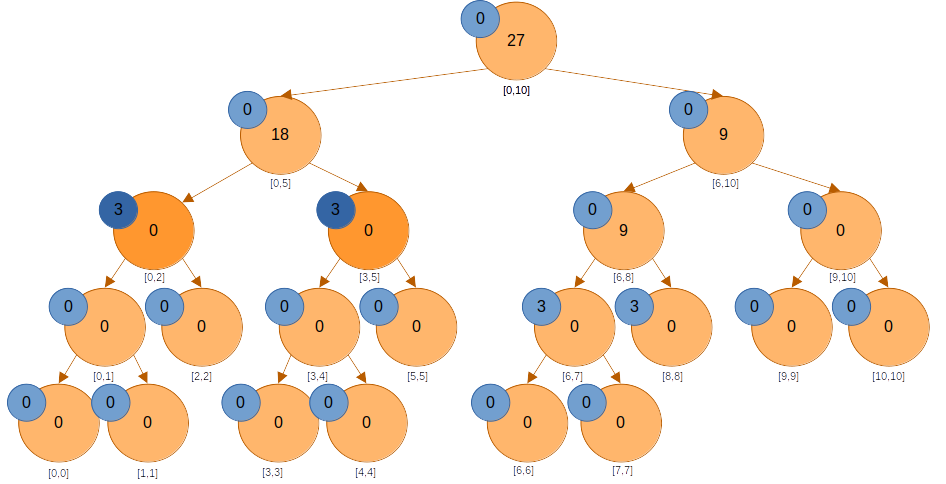
$[0, 2], [3, 5]$에는 미반영된 값이 있으니 반영해줘야 한다. 값을 반영해주면 노드의 값도 바뀌고, 자식 노드들의 lazy 값도 변한다.

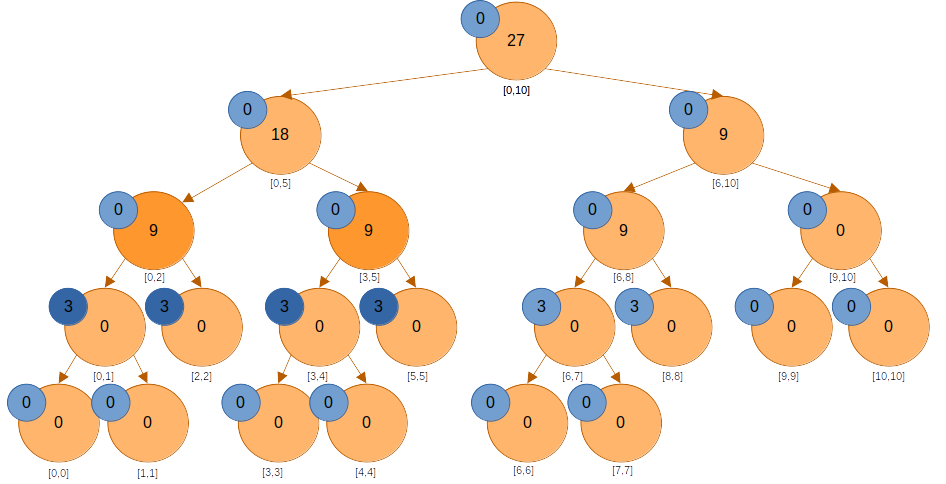
$[0,2]$는 쿼리 구간과 겹치지 않으니 0을 반환하고, $[3,5]$를 내려가본다.

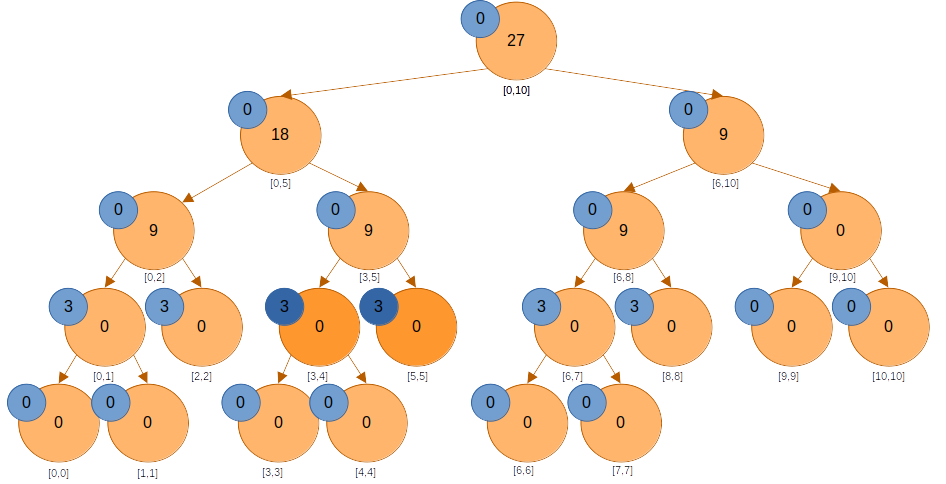
두 자식 노드들에 미반영된 값을 반영한다. $[3,4]$의 자식의 lazy도 바뀐다.

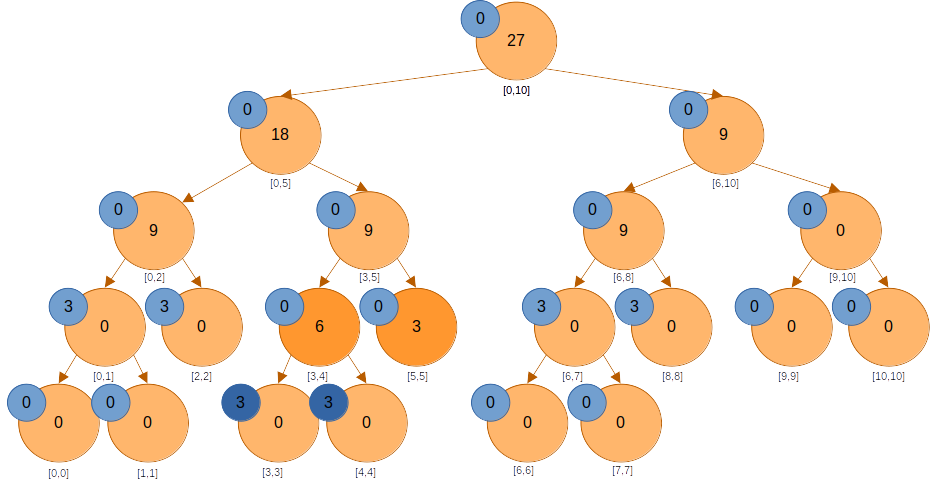
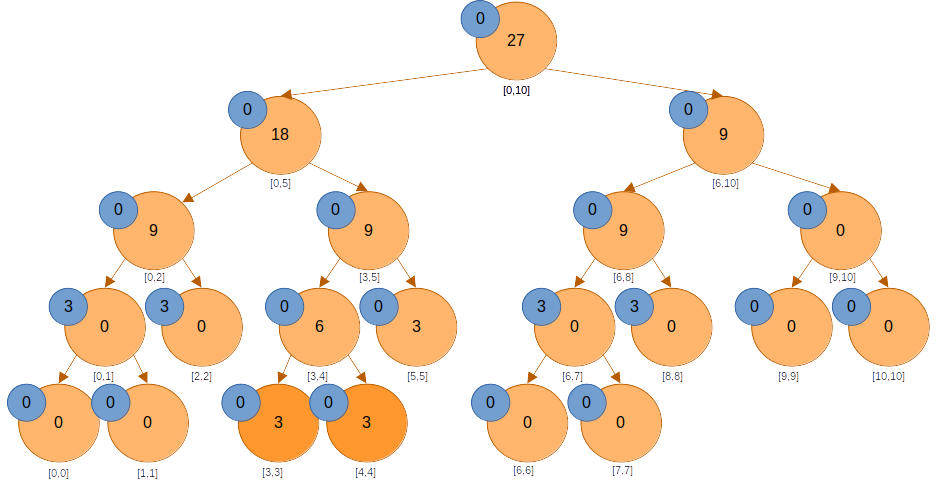
계속 내려가서 값을 반영시켜주면, 최종 결과는 아래와 같이 된다. $[4, 4]$까지 변경 사항이 반영됐고, 이제는 $[4, 4]$ 구간 쿼리에 대한 결과를 제대로 가져올 수 있게 된다.

3. Code

구간합을 관리하기 위한 세그먼트 트리라 할 때, 지연 전파를 사용하는 코드는 다음과 같다.

/**
* @brief [start, end] 구간의 값을 변경한다.
* @param node 노드의 인덱스
* @param start 해당 인덱스의 노드가 담당하는 구간의 시작 
* @param end 해당 인덱스의 노드가 담당하는 구간의 끝
*/
void propagate(int node, int start, int end) {
	if (lazy[node]) {
		tree[node] += (end - start + 1) * lazy[node];

		if (start != end) {//리프 노드가 아니라면 
			lazy[node * 2] += lazy[node];//왼쪽
			lazy[node * 2 + 1] += lazy[node];//오른쪽
		}

		lazy[node] = 0;//미반영된 값이 반영되었으니 초기화
	}
}

/**
* @brief [left, right] 구간의 모든 원소에 각각 val을 더한다
* @param node 노드의 인덱스
* @param start 해당 인덱스의 노드가 담당하는 구간의 시작 
* @param end 해당 인덱스의 노드가 담당하는 구간의 끝
* @param left 갱신하고자 하는 구간의 시작
* @param right 갱신하고자 하는 구간의 끝
* @param val 더할 값
*/
void update(int node, int start, int end, int left, int right, int val){
	propagate(node, start, end);//해당 노드에 미반영된 값이 있으면 반영시킨다. 
	if (right < start || end < left) return;
	if (left <= start && end <= right) {
		lazy[node] += val;//반영시킬 값을 적절히 바꾸고
		propagate(node, start, end);//반영시킨다.
		return;//그 아래로 내려갈 필요는 없다.
	}

	int mid = (start + end) / 2;
	update(node * 2, start, mid, left, right, val);
	update(node * 2 + 1, mid + 1, end, left, right, val);

	tree[node] = tree[node * 2] + tree[node * 2 + 1];
}

/**
* @brief [left, right] 구간의 합 
* @param node 노드의 인덱스
* @param start 해당 인덱스의 노드가 담당하는 구간의 시작 
* @param end 해당 인덱스의 노드가 담당하는 구간의 끝
* @param left 갱신하고자 하는 구간의 시작
* @param right 갱신하고자 하는 구간의 끝
*/
int query(int node, int start, int end, int left, int right){
	propagate(node, start, end);//미반영된 값이 있으면 반영
	if (right < start || end < left) return 0;
	if (left <= start && end <= right) return tree[node];

	int mid = (start + end) / 2;
	return query(node * 2, start, mid, left, right) + query(node * 2 + 1, mid + 1, end, left, right);
}

여기서 lazy 배열에 값을 어떻게 주고, 또 이 미반영된 값을 tree에 어떻게 반영시키느냐에 따라 다양한 문제들을 풀 수 있다.

4. 풀어볼 만한 문제

• 10999 구간 합 구하기 2 : 구간합 문제
• 12895 화려한 마을 : 비트마스킹 활용
• 1395 스위치 : 다양한 활용 1
• 18407 가로 블록 쌓기: 다양한 활용 2