[Algo] 폴라드 로(Pollard Rho) 인수분해 알고리즘

Park Yeongseo·2024년 4월 5일
algorithm알고리즘인수분해폴라드 로

Algorithm

목록 보기
7/20
post-thumbnail

폴라드 로 알고리즘은 1974년 폴라드가 만들어 낸, 합성수의 인수를 찾는 알고리즘이다. 이전에 작성한 이 글을 읽고 오기를 추천한다.

David.M.Burton의 Elementary Number Theory의 내용을 정리한 내용입니다.

1. 폴라드 로 알고리즘 (기본)

합성수로 알려진 큰 홀수 nn이 있다고 하자. 폴라드 로 알고리즘은 정수 계수를 가진, 최소 2차 이상의 간단한 다항식을 정하는 것으로부터 시작한다.

f(x)=x2+a,a≠0,−2f(x) = x^2 + a, a \neq 0, -2

함수 f(x)f(x)는 임의의 값 x0x_0 으로부터 시작해, 다음의 관계를 만족하는 유사 난수 수열 x1, x2, x3, ...x_1,\ x_2,\ x_3,\ ... 을 재귀적으로 만들어 내는 데 쓰인다.

xk+1≡f(xk)(mod  n)k=0, 1, 2, ...x_{k+1} \equiv f(x_k) (\mod n) \qquad k = 0,\ 1,\ 2,\ ...

정수 dd가 1이 아닌, nn보다 작은 nn의 약수라 하자. d<nd < n이므로 dd를 법으로 하는 합동류(congruence class)는 nn을 법으로 하는 합동류보다 작다. 그렇기 때문에 위 수열에는 다음을 만족하는 법 dd에 대해서는 같은 합동류에 속하지만 법 nn에 대해서는 다른 합동류에 속하는 xk, xjx_k,\ x_j 쌍이 있을 수 있다. 즉 다음을 만족하는 xk, xjx_k,\ x_j가 있을 수 있다.

xk≡xj(mod  d)xk≢xj(mod  n)\begin{aligned} x_k \equiv x_j(\mod d)\\ x_k \not\equiv x_j(\mod n) \end{aligned}

xkx_k와 xjx_j가 나머지 dd에 대해 합동이라는 것은 dd가 xk−xjx_k - x_j를 나눈다는 것이다. 한편 xkx_k와 xjx_j는 법 nn에 대해서는 합동이 아니므로, nn은 xk−xjx_k - x_j를 나누지 않는다. 따라서 gcd(xk−xj,n)gcd(x_k - x_j, n)은 1이 아닌 nn의 약수이다.

d∣n이므로 n=da이고, d∣(xk−xj)이므로 (xk−xj)=db라 할 수 있다.(a, b는 정수)n∤(xk−xj)이므로 gcd(xk−xj,n)은 d보다 크거나 같은, n이 아닌 정수다.\begin{aligned} &d | n이므로\ n= da이고,\ d | (x_k - x_j)이므로\ (x_k - x_j) = db라\ 할\ 수\ 있다.(a,\ b는\ 정수)\\ &n \not\mid (x_k-x_j)이므로\ gcd(x_k-x_j, n)은\ d보다\ 크거나\ 같은,\ n이\ 아닌\ 정수다. \end{aligned}

다만 실제로는 nn의 약수 dd에 대해서는 이외에 미리 알려진 게 없다. 하지만 정수 xkx_k를 계속 따라가다 보면 dd를 찾을 수 있을지도 모른다. xkx_k와 xjx_j (단 k>jk > j)를 비교하며 1이 아닌 gcd(xk−xj,n)gcd(x_k - x_j, n)이 나올 때까지 반복해보자.

그러나 이렇게 얻은 최대 공약수가 반드시 nn의 가장 작은 인수라는 보장은 없고, 더욱이 소수라는 보장은 없다. 또한 계산을 이어갔을 때 드물게 nn의 진약수가 아닌 nn이 나올 가능성도 있다. 이때는 다른 x0x_0 값이나 다른 다항식 f(x)f(x)를 사용해서 해결할 수 있다.

Example(1)

정수 n=2189n = 2189, x0=1x_0 = 1, f(x)=x2+1f(x) = x^2 + 1이라 하자. 이때 나타나는 수열은 다음과 같다.

x1=2, x2=5, x3=26, x4=677, x5=829, ...x_1 = 2,\ x_2 = 5,\ x_3 = 26,\ x_4 = 677,\ x_5 = 829,\ ...

수열에 나타나는 서로 다른 xkx_k를 서로 비교해보면 gcd(x5−x3,2189)=gcd(803,2189)=11gcd(x_5 - x_3, 2189) = gcd(803, 2189) = 11을 찾을 수 있다. 2189÷11=1992189 \div 11 = 199이므로 1111은 21892189의 인수임을 확인할 수 있다.

(CODE) 기본 폴라드 로

아래는 위에서 설명한 기본 폴라드 로를 구현한 코드다. 다만 int의 오버플로와 같은 문제는 따로 처리하고 있지는 않다.

#include <iostream>
#include <vector>
using namespace std;

vector<int> x;

int f(int x_k, int a, int n){//간단한 다항식
    return (x_k * x_k + a) % n;
}

int gcd(int a, int b){
    a = abs(a);
    b = abs(b);

    int r;

    if (a < b) swap(a, b);

    while (b){
        r = a % b;
        a = b;
        b = r;
    }

    return a;
}

int pollard_rho(int n){
    if (n == 1) return n;

    int a = rand() % (n - 2) + 2; // a는 n보다 작은, -2, 0이 아닌 정수여야 함 
    int x_0 = rand() % 20; //임의의 초항을 정한다

    x.push_back(x_0);//초항을 넣어주자

    while (true){
        int x_k = f(x.back(), a, n);//다음 항을 계산

        for (int x_j : x){//이전에 나온 모든 항들에 대해
            int g = gcd(x_k - x_j, n);//최대공약수를 계산해보자.

			if (g == n) {//드물게 일어나는 경우. 다시 계산해봐야 한다.
                x.clear();
                return pollard_rho(n);//다른 초항과 상수항으로 다시 시작해보자
            }
			else if (g != 1) {//non-trivial factor를 찾은 경우
                return g;
            }
        }

        x.push_back(x_k);
    }

    return n;
}

int main(){
    int n;//n은 합성수인 홀수.
    scanf("%d", &n);

    int p = pollard_rho(n);

    printf("%d %% %d = %d", n, p, n % p);
}

2. 최적화

문제는 kk가 커지면, 모든 j<kj < k에 대해 gcd(xk−xj,n)gcd(x_k - x_j, n)를 찾는 일이 너무 부담스러워진다는 것이다(위 코드의 39번 줄). 이를 보다 최적화하기 위해, k=2jk = 2j인 경우만을 고려해도 됨을 보이도록 하자.

dd가 nn보다 작은, 1이 아닌 nn의 약수라 하자. 만약 xk≡xj(mod  d)x_k \equiv x_j (\mod d)이면 f(x)f(x)가 선택된 방식에 따라,

xj+1=f(xj)≡f(xk)=xk+1(mod  d)x_{j+1} = f(x_j) \equiv f(x_k) = x_{k+1} (\mod d)

이다. 다시 말해 수열 {xk}\{x_k\}에 modulo dmodulo\ d를 적용한 수열은 언젠가 길이 k−jk-j 의 구간이 무한히 반복되는 수열이 된다. 즉 만약 r≡s(mod  (k−j))r \equiv s (\mod{(k -j)}) (r≥j,s≥j)(r \geq j, s \geq j) 이면, xr≡xs(mod  d)x_r \equiv x_s(\mod{d})이다. 특히 tt가 jj보다 큰 k−jk-j의 배수이면, x2t≡xt(mod  t)x_{2t} \equiv x_t(\mod{t})가 되고, 따라서 1<gcd(x2k−xk,n)<n1 < gcd(x_{2k} - x_k, n) < n인 정수 k가 있을 것이라 기대할 수 있다.

유일한 단점은 n의 자명하지 않은 인수인 gcd(xi−xj,n)gcd(x_i - x_j, n)가 처음으로 나타나는 때가 언제인지 바로 알 수 있는 것은 아니라는 점이다.

Example (2)

n=30623n = 30623을 인수분해하려 한다고 하자. x0=3,f(x)=x2−1x_0 = 3, f(x) = x^2 - 1이라 하면, 이로부터 만들 수 있는 수열은 다음과 같다.
8,63,3968,4801,21104,2856,18319,18926,...8, 63, 3968, 4801, 21104, 2856, 18319, 18926, ...
각 x2kx_{2k}와 xkx_k를 비교해보면 다음을 얻을 수 있다.

x2−x1=55gcd(55,n)=1x4−x2=4738gcd(55,n)=1x7−x3=24558gcd(24558,n)=1x8−x4=14125gcd(14125,n)=113\begin{aligned} &x2 -x1 = 55 \quad gcd(55, n) = 1\\ &x4 - x2 = 4738 \quad gcd(55, n) = 1\\ &x7-x3 = 24558 \quad gcd(24558, n) = 1\\ &x8 - x4 = 14125 \quad gcd(14125, n) = 113\\ \end{aligned}

113×271=30623113 \times 271 = 30623이므로 113이 30623의 인수임을 알 수 있다.

한편 위 수열에 각각 mod  113\mod{113}을 해주면 다음의 새로운 수열을 얻을 수 있다.
8,63,13,55,86,50,13,55,...8, 63, 13, 55, 86, 50, 13, 55, ...
이 수열에서는 13,55,86,5013, 55, 86, 50이 계속해서 반복된다. 이를 그림으로 나타내면 다음과 같다.

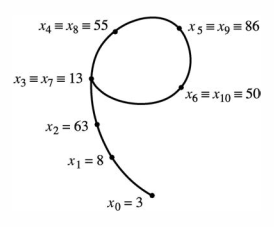
이 모양은 그리스 문자 ρ\rho와 닮아 있다. 여기서 소개한 폴라드의 인수분해 알고리즘을 가리켜 "폴라드 로 알고리즘"이라 부르는 이유다.

(CODE) 최적화 폴라드 로 코드

int pollard_rho(int n){
    if (n == 1) return n;

    int a = rand() % (n - 2) + 2; // a는 n보다 작은, -2, 0이 아닌 정수다. 
    int x_0 = rand() % 20; //임의의 초항을 정한다

    x.push_back(x_0);//초항을 넣어주자

    while (true){
        x.push_back(f(x.back(), a, n));//다음 항을 계산하고 넣어주기

        int k = x.size() - 1;
        if (k % 2) continue;//홀수 번째 항이라면 건너뛴다.

        int g = gcd(x[k] - x[k / 2], n);
        
        if (g == n) {//드물게 일어나는 경우. 다시 계산해봐야 한다.
            x.clear();
            return pollard_rho(n);//다른 초항과 상수항으로 다시 시작해보자
        }
        else if (g != 1) {//non-trivial factor를 찾은 경우
            printf("g: %d\n", g);
            return g;
        }
    }

    return n;
}

5. 남은 문제

폴라드 로 알고리즘에서 인수분해할 nn은 "합성수인 홀수"여야 한다. 위 코드를 실행해보면 알겠지만 nn이 소수인 경우는 제대로 동작하지 않는다.

따라서 임의로 입력되는 nn이 합성수인지 아닌지도 모르는 경우에는 이를 판별할 방법도 있어야 한다. 임의의 큰 정수 nn의 소수 여부를 확인하기 위한 알고리즘으로는 다음으로 포스팅될 밀러-라빈 소수판별법(Miller-Rabin primality test)이 있고, 이 알고리즘을 폴라드 로와 조합해 임의의 큰 정수 nn의 소인수분해도 할 수 있다.

profile
Park Yeongseo
이전 포스트

[Algo] 그레이엄 스캔 (Graham Scan)

다음 포스트

[Algo] 밀러-라빈 소수 판별법(Miller-Rabin Primality Test)

0개의 댓글