1. 세그먼트 트리

세그먼트 트리(segment tree)는 연속된 구간 내 데이터에 대한 쿼리를 빠르게 처리할 수 있는, 이진 트리 기반의 자료 구조다.

예를 들어 길이 N의 배열이 있다고 하자. 이 배열의 특정 구간을 대표할 수 있는 값, 예컨대 구간 내 원소의 합, 곱, 최댓값, 최솟값 등을 묻는 쿼리가 반복적으로 주어진다고 하자. 세그먼트 트리를 이용하면 이 쿼리들을 $O(\log{N})$의 시간에 처리할 수 있다.

물론, 예를 들어 구간합의 경우, 흔히 사용하는 누적합 이용하면 $O(1)$의 시간에 쿼리를 처리할 수도 있다. 하지만 주어진 배열에서 새 값으로의 갱신도 일어나는 경우가 있다면 어떨까? 누적합의 경우, 한 원소의 변화가 해당 원소의 인덱스 이후의 누적합에도 영향을 주어야 하기에, 변화가 전체에 제대로 반영되기 위한 시간복잡도는 $O(N)$이라 할 수 있다. 한편 세그먼트 트리를 사용하는 경우, 한 원소의 변화가 전체에 반영되는 데에는 $O(\log{N})$의 시간이 걸린다.

세그먼트 트리는 이런 구간에 대한 쿼리 및 원소 갱신이 필요한 경우에 유용하게 쓸 수 있고, 구현만 조금씩 바꿔주면 여러 문제들에 적용할 수 있기 때문에(ex. 합, 곱, 최대, 최소 등등), 말 그대로 솔브닥 점수가 복사되는, 점수 복사기라 할 수 있다.

1) 개념

세그먼트 트리의 기본 아이디어는 다음과 같이 정리할 수 있겠다.

(1) 트리의 각 노드는 특정 구간을 담당한다.
(2) 노드의 왼쪽 자식은 구간의 왼쪽 절반, 오른쪽 자식은 나머지 절반을 담당한다.

(1) 트리의 각 노드는 특정 구간을 담당한다

세그먼트 트리를 이루는 각 노드는 특정 구간을 담당하며, 해당 노드에는 그 노드가 담당하는 구간의 대표값(합, 곱, 최대, 최소 등등)이 들어 있다.

길이 $11$의 배열을 예로 생각해보자. 루트 노드는 전체 구간, 인덱스로 말하자면 $[0, 10]$의 구간을 담당한다.

(2) 노드의 왼쪽 자식은 구간의 왼쪽 절반, 오른쪽 자식은 구간의 나머지 절반을 담당한다.

앞서 세그먼트 트리는 이진 트리에 기반한 자료 구조라 했다. 즉 각 노드는 최대 2개의 자식 노드를 가질 수 있다. 노드의 왼쪽 자식은 구간의 왼쪽 절반, 오른쪽 자식은 구간의 오른쪽 절반을 담당하도록 구성한다.

단 이때 부분 구간의 대표값들을 가지고서 해당 노드의 대표값을 찾을 수 있음이 보장되어야 한다. 예를 들어 $[0, 10]$의 구간합은 $[0, 5]$의 구간합과 $[6, 10]$의 구간합이다. 다른 예로, $[0, 10]$의 최댓값은 $[0,5]$의 최댓값과 $[6, 10]$의 최댓값 중 최대다.

$[0, 10]$의 구간을 반으로 나눠보자. 길이가 11이니, 왼쪽 자식이 담당하는 구간의 길이는 6, 오른쪽 자식이 담당하는 구간의 길이는 5가 된다. 트리로 그리면 다음과 같다.

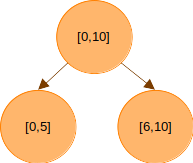
$[0, 5]$의 구간은 또 $[0, 2], [3,5]$의 구간으로 나눌 수 있다.

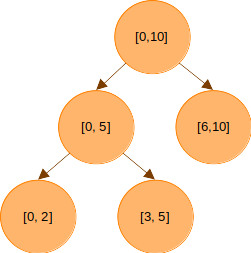
마찬가지로 $[6, 10]$도 반으로 나눌 수 있다. 더 이상 구간을 나눌 수 없을 때까지 나눠 가며 트리를 만든 결과는 다음과 같다.

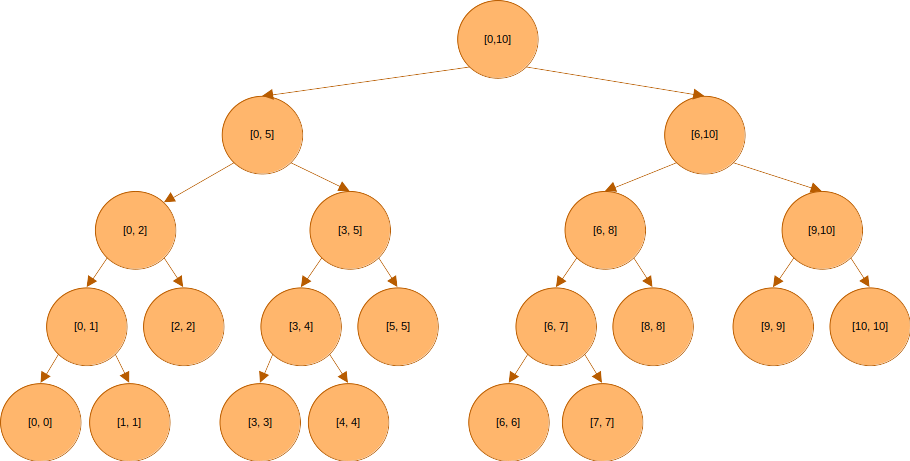
2) 구간 쿼리

세그먼트 트리에서 특정 구간의 대푯값을 찾는 쿼리는 $O(\log{N})$의 시간에 처리될 수 있다.

만약 $[2, 8]$ 구간의 대푯값을 알고 싶다면 어떤 노드의 값들을 알아야 할까?

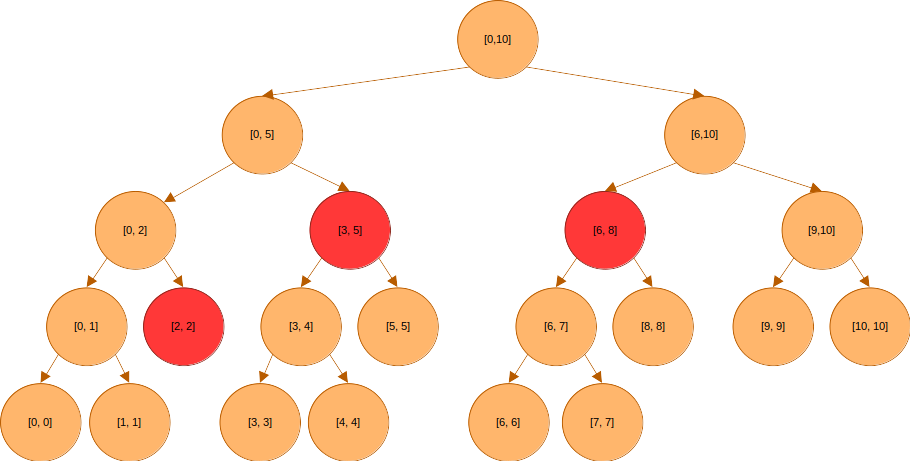
$[2, 7]$ 구간의 대푯값을 알고 싶다면, $[2,2], [3, 5], [6, 8]$ 구간을 담당하는 세 노드의 값만 알면 된다. 부분 구간의 대표값들을 가지고서 그것들을 합친 구간의 대표값을 찾을 수 있음이 보장되기 때문이다.

$[0, 8]$ 구간을 알고 싶다면 어떨까?

$[0, 8]$을 알고 싶다면 $[0, 5], [6, 8]$만 알면 된다.

그렇다면 이 노드들은 어떻게 찾을 수 있을까? 정답은 간단하다.

루트에서 시작해 내려가면서 처음으로 만나게 되는, 쿼리 구간에 완전히 포함되는 노드들을 찾아낸다.

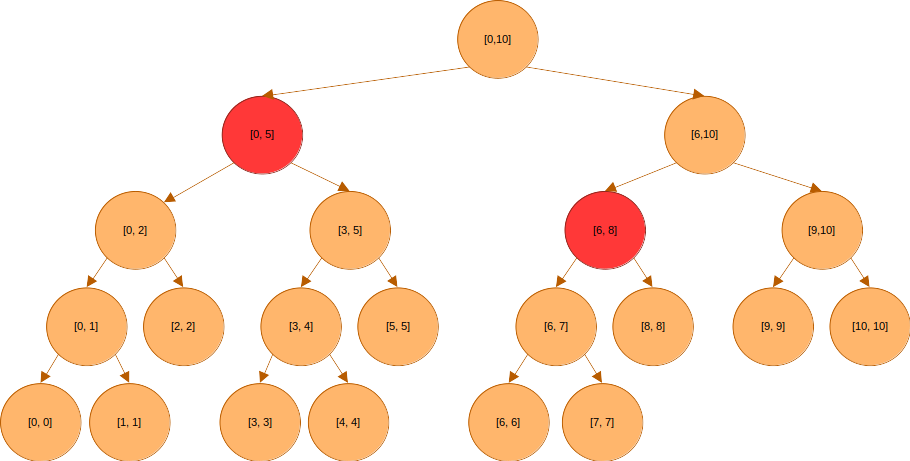
다시 $[2, 8]$의 대푯값을 찾으려 한다고 해보자.

루트는 $[0, 10]$의 구간을 커버한다.

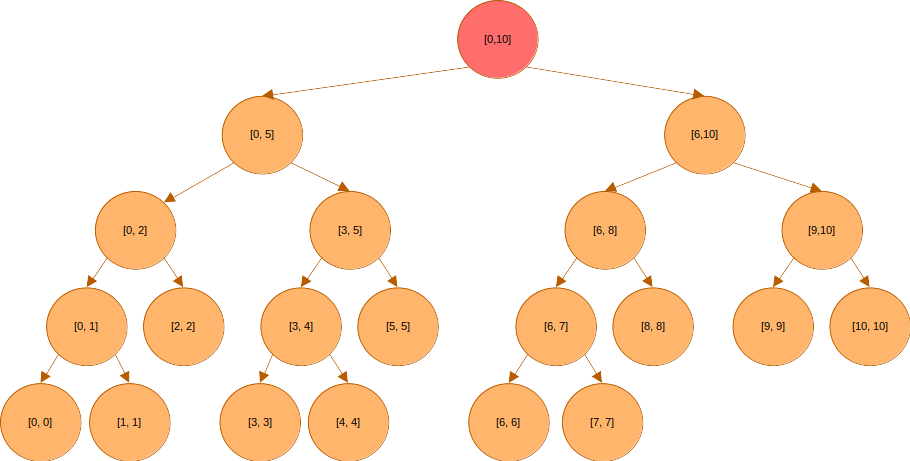
이 구간은 쿼리 구간 $[2, 8]$에 포함되지 않으니 아래로 내려가야 한다.

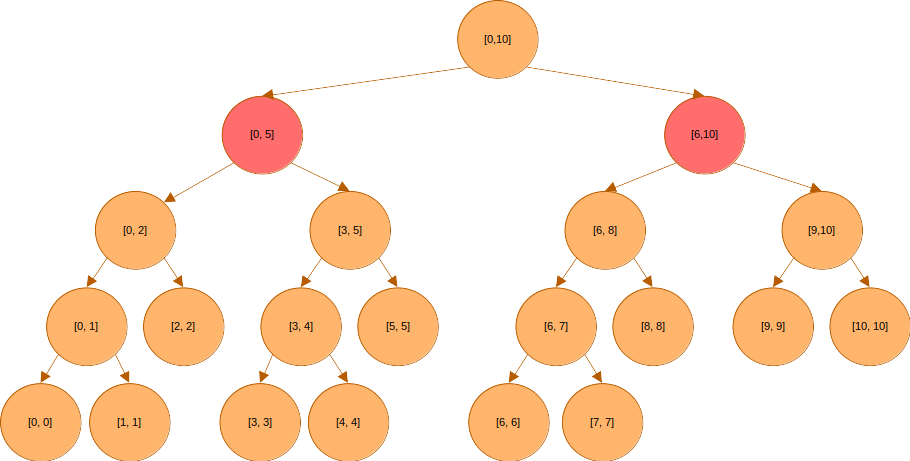
$[0, 5]$와 $[6, 10]$도 쿼리 구간에 포함되지 않기는 마찬가지다. 내려가야한다.

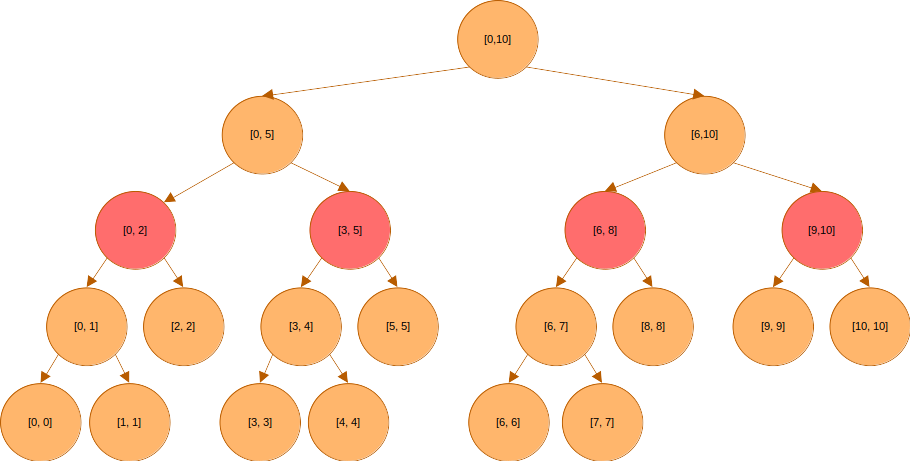
$[3, 5]$와 $[6, 8]$은 쿼리 구간에 포함되어 있다. 따라서 더 아래로 탐색을 하지 않는다.
쿼리 구간과 겹치는 부분이 있는 $[0,2]$의 경우 아래로 더 탐색을 해야 하지만, $[9, 10]$은 쿼리 구간과 겹치지 않으므로 탐색을 더 할 필요가 없다.

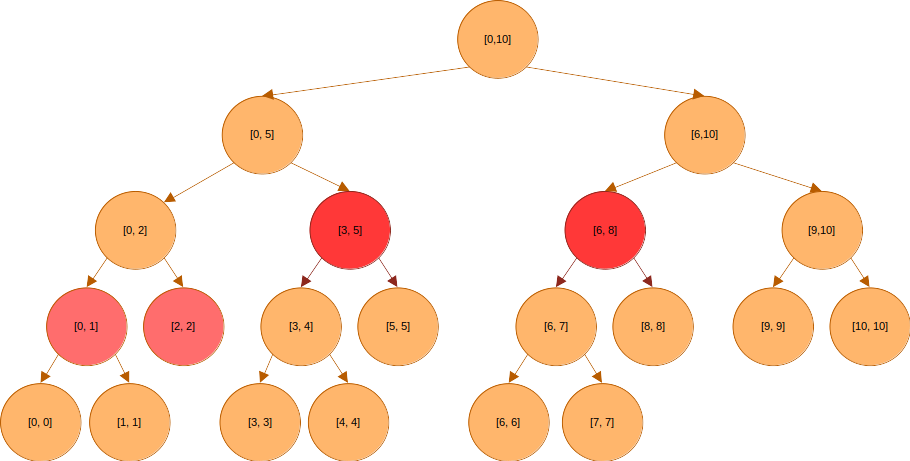
$[0,1]$은 쿼리 구간과 겹치지 않으므로 더 이상 탐색할 필요가 없고, $[2, 2]$는 쿼리 구간에 포함되어 있다.

$[2, 8]$ 구간의 대푯값에 대한 쿼리를 처리하기 위해 필요한 노드들을 모두 찾았다. 이 노드들에 담긴 세그먼트 트리(segment tree)는 연속된 구간 내 데이터에 대한 쿼리를 빠르게 처리할 수 있는, 이진 트리 기반의 자료 구조다. 예를 들어 길이 N의 배열이 있다고 하자. 이 배열의 특정 구간을 대표할 수 있는 값, 예컨대 구간 내 원소의 합, 곱, 최댓값, 최값을 이용하면 $[2, 8]$ 구간의 대푯값을 찾을 수 있다.

3) 갱신

주어진 배열에서 특정 원소의 값이 변하는 경우가 있다고 해보자. 예를 들어, 위의 예에서 3번 원소의 값이 변했다고 해보자.

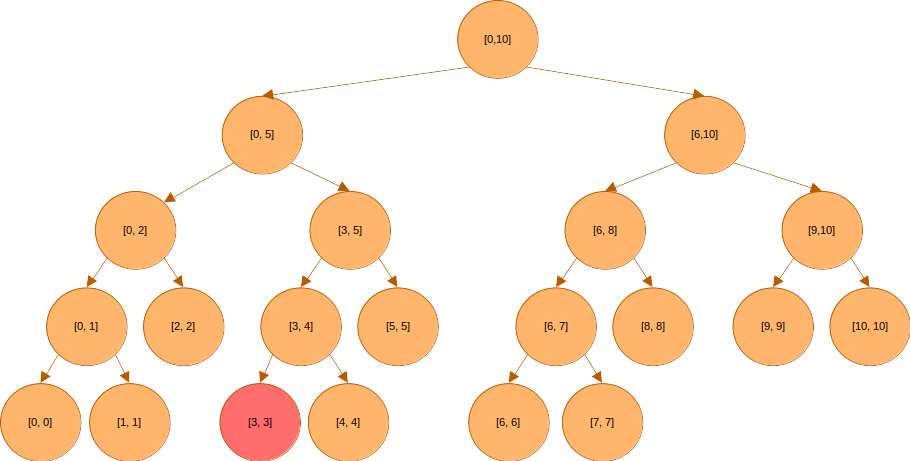
3번 원소의 값이 변하는 경우, 3번이 포함된 구간을 커버하는 모든 노드의 값도 변해야 한다. 즉 아래에 표시된 모든 노드들의 값이 변해, 3번 원소의 변화를 반영할 수 있어야 한다.

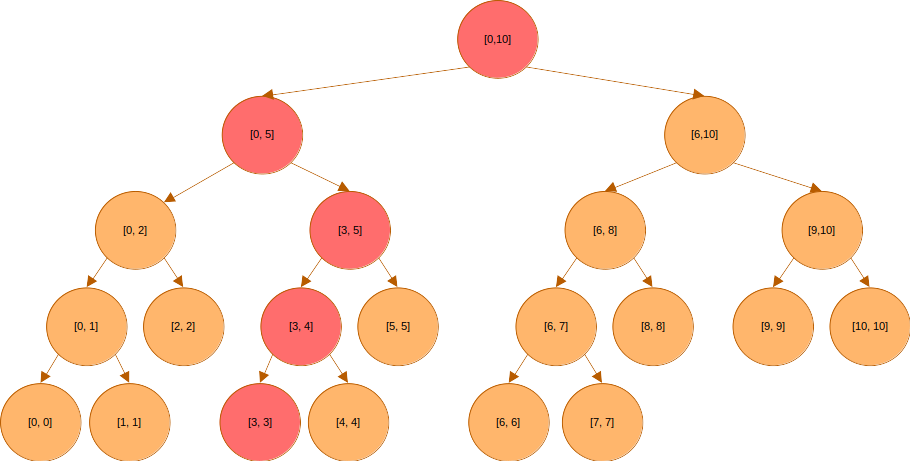
이 노드들은 구간 쿼리에서와 마찬가지의 방법으로 찾을 수 있다.

루트에서 시작해 리프 노드까지 내려가면서, 변경하고자 하는 원소 인덱스를 포함하는 구간들을 모두 갱신한다.

세그먼트 트리에서 원소 하나의 값을 갱신하고, 그 변화가 해당 원소를 포함하는 구간 전체에 반영시키는 데에는 $O(\log{N})$의 시간이 걸린다.

한편, 위와 같이 한 원소의 값만 변경하는 게 아니라, 특정 구간에 속한 모든 원소들의 값을 일괄적으로 변경할 수도 있다. 이때에는 갱신하고자 하는 구간과 겹치는 구간들을 모두 갱신해주어야 한다. 갱신하고자 하는 구간 내의 모든 원소들을 각각 갱신시켜 준다고 생각해도 좋다.

예를 들어 $[2, 4]$ 구간을 갱신한다고 해보자. 이때 값이 변해야 할 노드들은 다음과 같다.

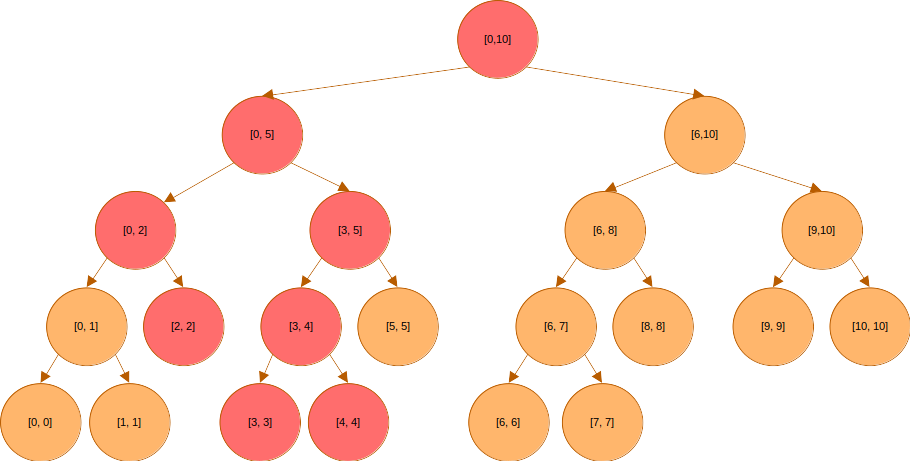
이때 만약 변경하고자 하는 구간의 길이가 $L$이라면, 해당 구간 내 원소들을 일괄 변경하는 데 걸리는 시간은 $O(Llog{N}) = O(Nlog{N})$이 될 것이다.

2. 세그먼트 트리의 구현 (C++)

관리하고자 하는 배열의 길이가 $N$이라 하자. 이를 관리하기 위해 필요한 세그먼트 트리 노드의 개수는 최소 $2N - 1$개이며, 물론 이 $2N-1$개의 노드만을 이용해서 세그먼트 트리를 만드는 것도 가능하다.

하지만 보통은 힙을 구현할 때처럼 1차원 배열을 이용해 구현한다.

• 일차원 배열을 이용해 구현한다.
• 루트 노드의 인덱스는 1이다.
• 왼쪽 자식의 인덱스는 부모 인덱스 2, 오른쪽 자식의 인덱스는 부모 인덱스 2 + 1이 된다.

이렇게 세그먼트 트리를 구현하기 위해 사용하는 1차원 배열의 크기는 얼마여야 할까? 앞의 예제를 다시 살펴 보고, 위의 방식대로 각 노드에 번호를 매겨보면 다음과 같다.

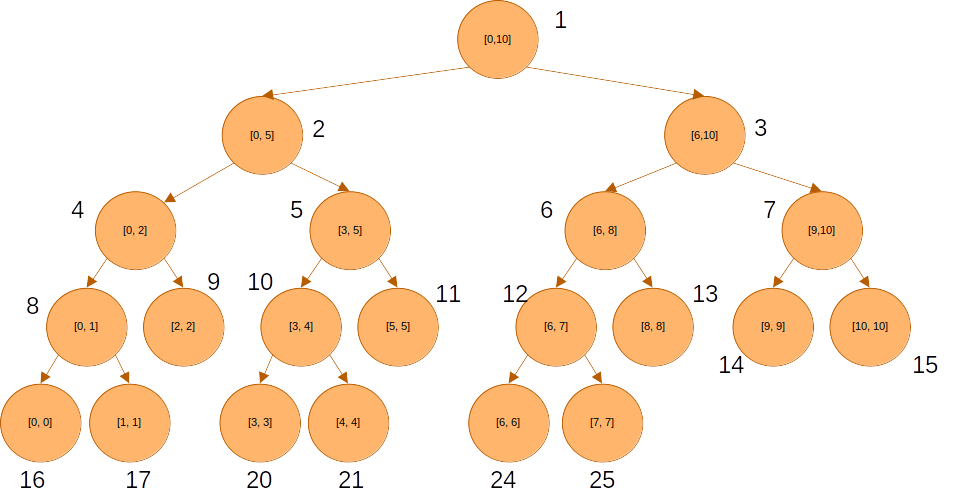
이렇게 각 노드에 번호를 매겨 보면, 마지막 노드의 번호가 25이므로 크기가 26인 1차원 배열을 이용하면 $[0, 10]$ 구간을 관리하는 세그먼트 트리를 만들 수 있다. 하지만 주어진 길이의 배열을 관리하는 세그먼트 트리의 마지막 노드 번호가 정확히 무엇이 될지 계산하는 것은 번거롭다.

위 트리를 포화 이진트리로 생각해보자.

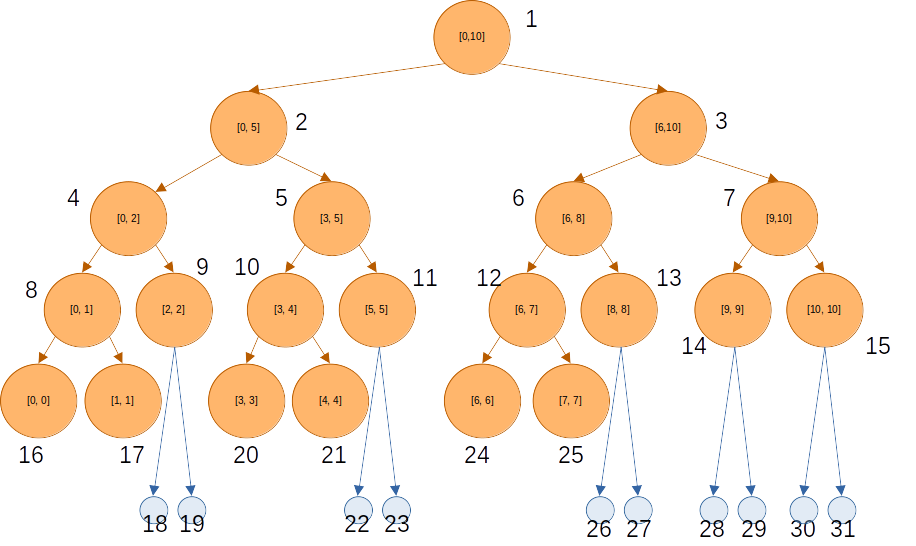
9, 11, 13, 14, 15번 노드의 경우, 구현 상으로는 좌우 자식들을 가지지만, 실제로 더 이상 탐색은 일어나지 않는다고 생각할 수 있다.

이렇게 생각하면, 세그먼트 트리를 1차원 배열로 구현할 때의 마지막 노드 번호를 따로 계산하지 않고, 1차원 배열의 크기를 ($N$보다 크거나 같은 가장 작은 2의 제곱수) * 2로 두기만 하면 된다.

더 쉽게는, ($N$보다 크거나 같은 가장 작은 2의 제곱수) * 2 $\leq$ $4N$임을 이용해, 간단히 1차원 배열의 크기를 $4N$으로 두어 사용해도 좋다.

int segtree[4 * N];//세그먼트 트리를 구현하기 위해 쓰이는 1차원 배열 

이하 구현에서는 주어진 배열의 구간합을 관리하기 위해 세그먼트 트리를 사용한다고 가정하자.

(1) 구간 갱신 코드

구간을 갱신하려면 갱신하고자 하는 구간과 겹치는 구간들을 모두 갱신해주어야 한다.

/**
* @brief [left, right] 구간의 모든 원소에 각각 val을 더한다
* @param idx 노드의 인덱스
* @param start 해당 인덱스의 노드가 담당하는 구간의 시작 
* @param end 해당 인덱스의 노드가 담당하는 구간의 끝
* @param left 갱신하고자 하는 구간의 시작
* @param right 갱신하고자 하는 구간의 끝
* @param val 더할 값
*/
void update(int idx, int start, int end, int left, int right, int val) {
	// 노드의 담당 구간과 갱신하고자 하는 구간이 전혀 겹치지 않는 경우다
	if (right < start || end < left) return;

	// start == end인 경우, 즉 주어진 배열의 원소 하나를 가리킨다.
	// 그 아래로의 탐색은 불필요하므로 값을 갱신한 후 즉시 리턴한다
	if (start == end) {
		segtree[idx] += val;
		return;	
	}
	
	int mid = (start + end) / 2;

	//왼쪽 자식의 인덱스는 부모 인덱스 * 2이고, 그 담당 구간은 부모가 담당하는 구간의 왼쪽 절반이다. 왼쪽 절반 구간의 구간합이 구해진다.
	update(idx * 2, start, mid, left, right, val);	

	//오른쪽 자식의 인덱스는 부모 인덱스 * 2 + 1이고, 그 담당 구간은 부모가 담당하는 구간의 오른쪽 절반이다. 오른쪽 절반 구간의 구간합이 구해진다.
	update(idx * 2 + 1, mid + 1, end, left, right, val);	

	//이 노드가 담당하는 구간의 구간합은 왼쪽 절반 구간의 구간합 + 오른쪽 절반 구간의 구간합과 같다.
	segtree[idx] = segtree[idx * 2] + segtree[idx * 2 + 1];
}

(2) 구간 쿼리 코드

특정 구간에 대한 쿼리를 처리할 떄에는 루트에서 시작해 내려가면서 처음으로 만나게 되는, 쿼리 구간에 완전히 포함되는 노드들을 찾아낸다.

/**
* @brief [left, right] 구간의 모든 원소의 합을 구한다
* @param idx 노드의 인덱스
* @param start 해당 인덱스의 노드가 담당하는 구간의 시작 
* @param end 해당 인덱스의 노드가 담당하는 구간의 끝
* @param left 쿼리 구간의 시작
* @param right 쿼리 구간의 끝
* @return [left, right] 구간의 구간합
*/
int query(int idx, int start, int end, int left, int right){
	// 노드의 담당 구간과 갱신하고자 하는 구간이 전혀 겹치지 않는 경우다.
	if (right < start || end < left) return 0;

	// 쿼리 구간에 완전히 포함되는 노드를 찾아낸 경우, 해당 값을 리턴한다.
	if (left <= start && end <= right) return segtree[idx];

	int mid = (start + end) / 2;

	// 왼쪽 절반 구간의 구간합을 구하고 오른쪽 절반 구간의 구간합을 구한 후 둘을 더해 반환한다.
	return query(idx * 2, start, mid, left, right) 
			+ query(idx * 2 + 1, mid + 1, end, left, right);
}

3. 지연 전파

이렇게 구간 갱신 및 구간 쿼리를 처리할 수 있게 됐다. 그런데 구간 갱신에는 한 가지 해결해야 할 문제가 있다. 바로 변경하고자 하는 구간의 길이가 $L$일 때, 해당 구간 내 원소들을 일괄 변경하는 데 걸리는 시간이 $O(Llog{N})$이 된다는 것이다. 예를 들어 아래와 같이 전체 구간을 갱신해야 하는 경우, 그 시간 복잡도는 $O(Nlog{N})$이 된다.

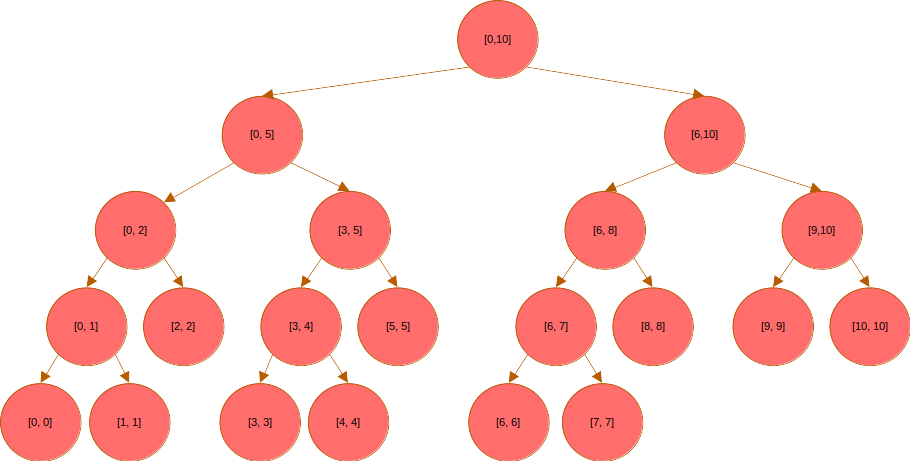
주어진 구간의 모든 원소에 특정 값을 더하는 연산, 그리고 특정 구간의 구간합을 묻는 문제가 있다고 하자. 일반적인 누적합을 이용하는 경우, 구간 갱신의 시간복잡도는 $O(N)$이고, 구간합 쿼리 처리의 시간복잡도는 $O(1)$이 된다.

구간 내 원소들을 일괄적으로 갱신하는 데 걸리는 $O(Nlog{N})$의 시간은, 그냥 naive하게 모든 원소들에 순차적으로 값을 더해주는 것보다도 느리다.

이러한 문제를 해결하기 위해 쓰이는 알고리즘이, 구간 갱신을 $O(log{N})$에 가능케 하는 지연 전파(lazy propagation)다. 이에 대한 내용은 다음에.