문제

1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다. (단, 시작점은 계단에 포함되지 않는다.)
3. 마지막 계단은 반드시 밟아야 한다.

풀이 과정

처음에 생각해낸 점화식은 다음과 같다.
이 경우, 연속으로 3개를 밟았는지 여부를 확인할 수 없기 때문에 틀린 점화식이었다.

$\text{정답} = \max(\text{DP}[N-1], \text{DP}[N-2])$

GPT로부터 힌트를 얻어보았다.

💡 GPT의 힌트

상태 정의에 '연속 횟수' 포함하기이 문제를 해결하는 핵심 힌트는 DP 테이블의 정의를 확장하는 것입니다.현재 계단 $i$를 밟았을 때의 최대 점수를 저장하는 것뿐만 아니라, 직전에 몇 개의 계단을 연속으로 밟았는지에 대한 정보도 함께 저장해야 합니다.

GPT의 힌트를 바탕으로 점화식을 수정해보았다.

"연속된 세 개의 계단을 모두 밟아서는 안 된다." 핵심은 2번 규칙이다. 이를 처리하기 위해 DP 테이블을 2차원 리스트로 확장시켰다.

일반적인 DP 문제처럼 DP[i]를 'i번째 계단까지의 최대 점수'로 정의하면 연속 3칸 금지 규칙을 적용할 수 없다. 따라서 i번째 계단을 밟을 때, 직전에 몇 개의 계단을 연속으로 밟았는지에 대한 정보를 DP 테이블에 추가해야한다.

DP 테이블을 2차원 배열로 정의합니다: DP[i][j]

• i: 현재 위치한 계단의 번호.
• j: $i$번째 계단을 밟는 것이 연속 몇 번째 계단인지 (1 또는 2).

DP 정의	의미
DP[i][1]	$i$번째 계단을 밟았고, 연속 1번째로 밟았을 때의 최대 점수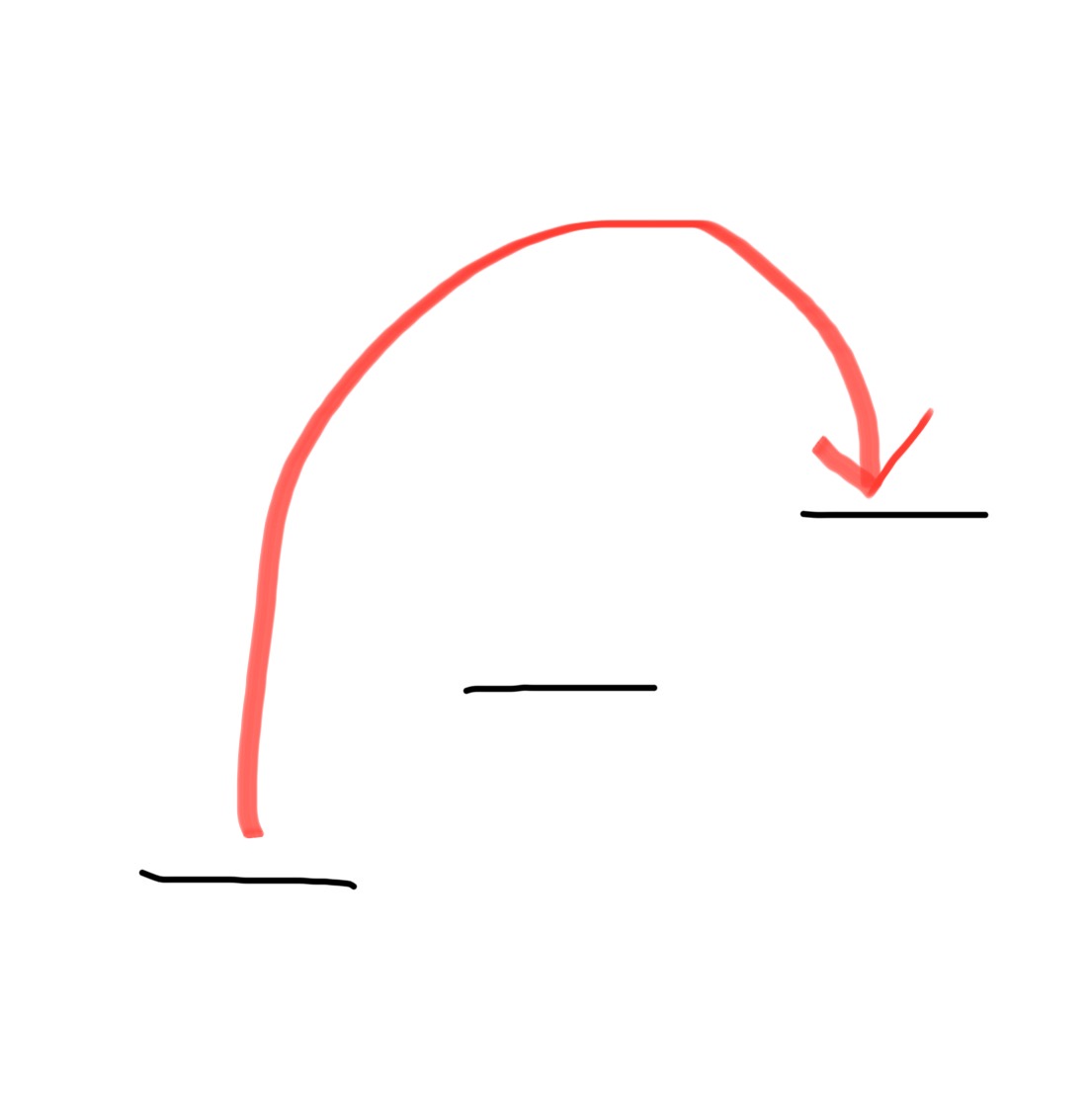
DP[i][2]	$i$번째 계단을 밟았고, 연속 2번째로 밟았을 때의 최대 점수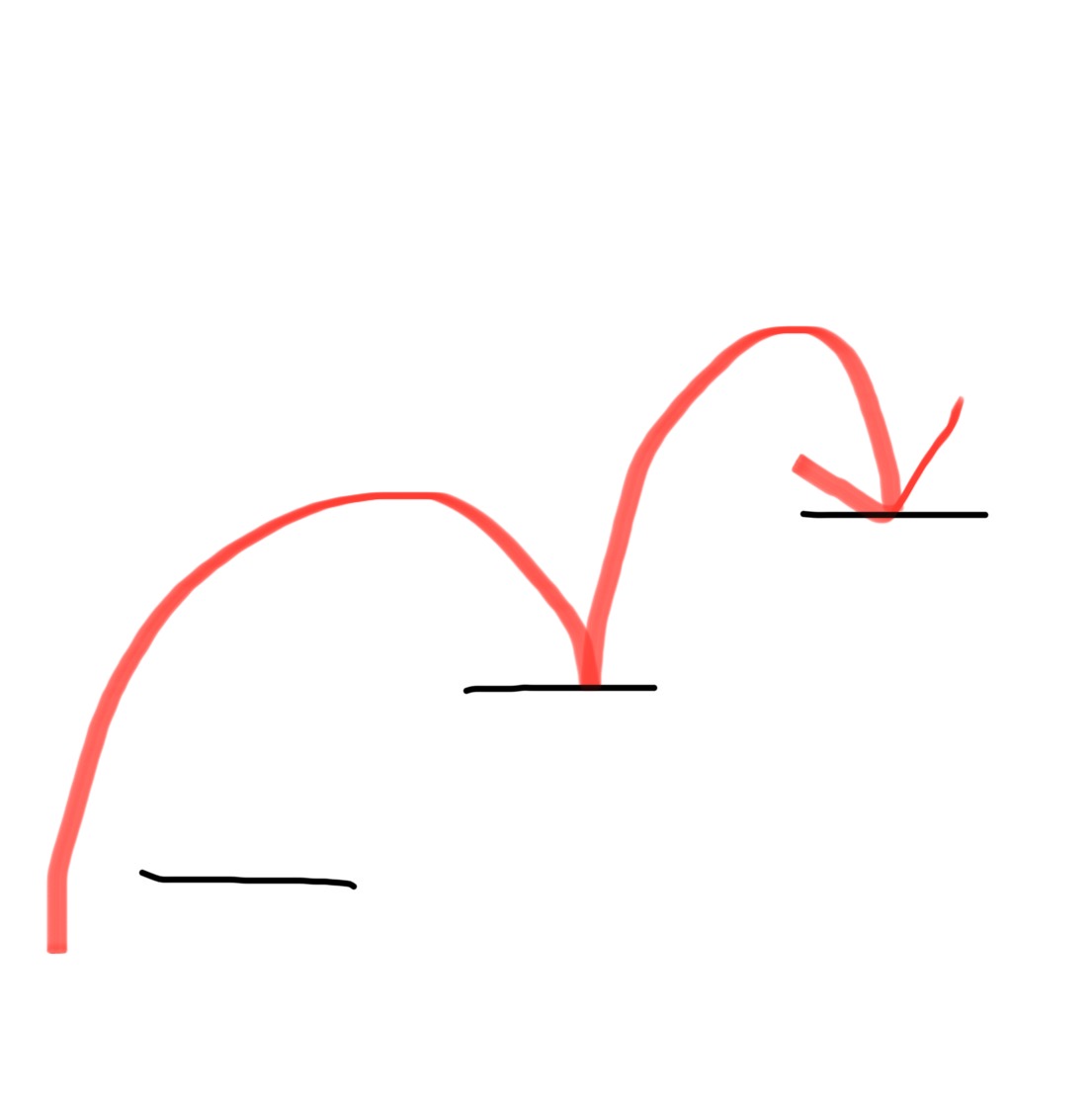

(연속 3번째는 규칙 위반이므로 연속 2번째까지만 정의한다.)

📝 점화식 유도: 경우의 수 나누기

$i$번째 계단의 점수를 stairs[i]라고 할 때,

1. DP[i][1]을 계산하는 경우 (i를 연속 1번째로 밟음)

$i$를 연속 1번째로 밟았다는 것은 직전 계단 ($i-1$)을 건너뛰고 $i$로 왔다는 의미입니다. 즉, $i-2$번째 계단에서 2칸을 점프해서 $i$로 온 경우만 해당됩니다.

이때 $i-2$까지의 최대 점수는 $i-2$가 연속 1번째든 2번째든 상관없으므로, 두 경우 중 더 큰 값을 선택합니다.

$\text{DP}[i][1] = \max(\text{DP}[i-2][1], \text{DP}[i-2][2]) + \text{stairs}[i]$

2. DP[i][2]을 계산하는 경우 (i를 연속 2번째로 밟음)

$i$를 연속 2번째로 밟았다는 것은 직전 계단 ($i-1$)을 밟고 1칸 전진해서 $i$로 왔다는 의미입니다.

연속 3개를 피하기 위해서는 $i-1$을 밟는 것이 반드시 연속 1번째였어야 합니다. ($i-1$이 연속 2번째였다면, $i-2$, $i-1$, $i$가 되어 3개가 됩니다.)

$\text{DP}[i][2] = \text{DP}[i-1][1] + \text{stairs}[i]$

🌟 최종 결과

최종적으로 $N$번째 계단까지 도달했을 때의 최대 점수는 $N$번째 계단을 연속 1번째로 밟았을 때와 연속 2번째로 밟았을 때의 두 가지 경우 중 더 큰 값입니다.

$\text{정답} = \max(\text{DP}[N][1], \text{DP}[N][2])$

이 문제처럼 제약 조건이 '연속 횟수'에 관련된 경우, DP 테이블의 상태를 확장하여 연속 횟수 정보를 포함하는 것이 핵심 전략입니다!

---

💻 최종 Python 풀이 코드

n = int(input())
stairs = [0] * (n+1)
# DP 테이블 정의: DP[i][j], j는 연속 횟수 (1 또는 2)
dp = [[0] * 3 for _ in range(n+1)]

# 계단 점수 입력
for i in range(1, n+1):
    stairs[i] = int(input())

# 초기값 설정 (1번째 계단)
dp[1][1] = stairs[1]

# 2번째 계단부터 최종 점화식 적용
for i in range(2, n+1):
    dp[i][1] = max(dp[i-2][1], dp[i-2][2]) + stairs[i]
    dp[i][2] = dp[i-1][1] + stairs[i]

print(max(dp[n][1], dp[n][2]))

1번째 계단은 무조건 연속 1번째이므로 DP[1][1]만 유효하다.