문제

https://www.acmicpc.net/problem/9461

---

풀이 과정

문제 분석: 숨겨진 점화식 찾기

문제에서 제시된 수열 $P(N)$의 초기 값들을 나열해 봅시다.

$N$	$P(N)$
1	1
2	1
3	1
4	2
5	2
6	3
7	4
8	5
9	7
10	9

이 수열의 값을 자세히 관찰하여 현재 항 $P(N)$을 이전 항들의 합으로 표현할 수 있는지 확인하는 것이 핵심.

🔎 규칙 발견 과정 (핵심 아이디어)

$P(N)$을 자세히 봐보자.
[1, 1, 1, 2, 2, ,3, 4, 5, 7, 9, ...]로 [1, 1, 1, 2, 2, ...] 이후부터는 값이 중복되지 않고 달라지는 것에 주목했다.

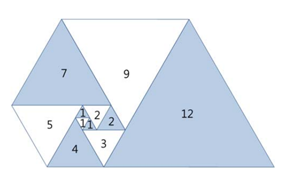
P의 초기값을 [1, 1, 1, 2, 2] 으로 설정한 후, P(6)부터 어떤 변의 합으로 이루어지는지를 적어보았다.

• $P(6) = 1 + 2 = 3$
• $P(7) = 1 + 3 = 4$
• $P(8) = 1 + 4 = 5$
• $P(9) = 2 + 5 = 7$
• $P(10) = 2 + 7 = 9$

이를 일반화하면, $N$번째 항은 $N-1$번째 항과 $N-5$번째 항의 합으로 이루어진다는 규칙을 발견할 수 있었다.

$\text{파도반 수열 점화식: } P(N) = P(N-1) + P(N-5) \quad (N \ge 6)$

참고: 이 문제의 정식 점화식은 $P(N) = P(N-2) + P(N-3)$ 이지만,
내가 발견한 $P(N) = P(N-1) + P(N-5)\quad (N \ge 6)$ 역시 파도반 수열을 계산하는 유효한 규칙이다! 두 규칙 모두 수열의 정의상 성립하며, 초기 값만 정확하다면 동일한 결과를 도출한다.

---

코드

T = int(input())
N = []
for i in range(T):
    N.append(int(input()))


p = [0, 1, 1, 1, 2, 2]
s = 1
e = 5

for i in range(max(N) - e):
    p.append(p[e] + p[s])
    s += 1
    e += 1

for i in N:
    print(p[i])

💻 코드 설명

여러분이 제시한 코드의 논리는 다음과 같습니다.

1. 초기 값 설정:
   • 파도반 수열의 초기 값을 p 리스트에 저장합니다. $P(0)$은 정의되지 않지만, 계산의 편의를 위해 0을 넣고 $P(1)$부터 $P(5)$까지의 값을 [0, 1, 1, 1, 2, 2]로 설정했습니다.
2. 규칙 적용 (슬라이딩 윈도우 개념):
   • $P(6)$부터 필요한 수열을 계산합니다. $P(6)$을 계산할 때 $P(1)$과 $P(5)$를 사용해야 합니다.
   • 여러분의 코드에서 s (start, $P(N-5)$에 해당하는 인덱스)와 e (end, $P(N-1)$에 해당하는 인덱스)라는 두 개의 포인터를 사용했습니다.
   • 초기 상태: s = 1, e = 5 (이때 $P(6) = P[5] + P[1]$을 계산할 준비가 됩니다.)
   • 반복: 새로운 $P(i)$ 값을 계산할 때마다 p.append(p[e] + p[s])를 수행하고, 다음 계산을 위해 s와 e를 1씩 증가시켜 포인터를 이동시킵니다 (슬라이딩).

계산할 $P(N)$	s (인덱스)	e (인덱스)	계산 식
$P(6)$	1	5	$P[5] + P[1]$
$P(7)$	2	6	$P[6] + P[2]$
$P(8)$	3	7	$P[7] + P[3]$
$\dots$	$\dots$	$\dots$	$\dots$
$P(N)$	$N-5$	$N-1$	$P[N-1] + P[N-5]$

이러한 방식으로, 가장 큰 입력 $N$까지의 수열을 미리 계산(max(N) - e만큼 반복)해두고, 최종적으로 입력된 $N$에 해당하는 값을 출력하는 방식이다.

---

마무리

이 문제는 언뜻 보면 복잡한 나선 모양 때문에 어려워 보이지만, 숨겨진 규칙(점화식)만 찾아내면 Dynamic Programming(DP)을 활용해 간단하게 풀 수 있었다.