단순 삽입 정렬

단순 삽입 정렬
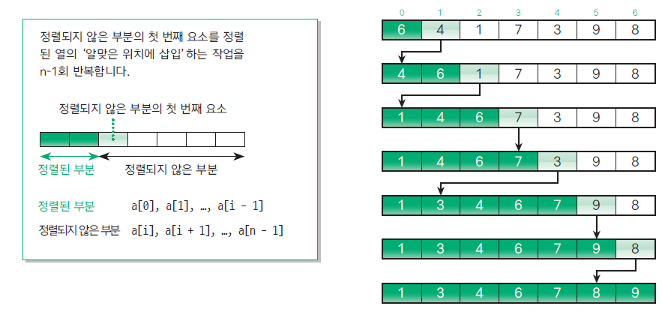
: 정렬되지 않은 부분의 첫 번째 요소를 정렬된 열의 '알맞은 위치에 삽입'하는 작업을 n-1회 반복한다.

- 2번째 요소부터 선택하여 진행한다.
- n-1회를 반복하여 정렬
- 셔틀 정렬(shuttle sort)이라고도 한다.

/* 단순 삽입 정렬 */
#include <stdio.h>
#include <stdlib.h>

/*--- 단순 삽입 정렬 함수 ---*/
void insertion(int a[], int n)
{
	int i, j;
	for (i = 1; i < n; i++) {
		int tmp = a[i];
		for (j = i; j > 0 && a[j - 1] > tmp; j--)
			a[j] = a[j - 1];
		a[j] = tmp;
	}
}

int main(void)
{
	int i, nx;
	int *x; 						/* 배열의 첫 번째 요소에 대한 포인터 */
	puts("단순 삽입 정렬");
	printf("요소수 : ");
	scanf("%d", &nx);
	x = calloc(nx, sizeof(int)); 	/* 요소의 개수가 nx인 int형 배열을 생성 */

	for (i = 0; i < nx; i++) {
		printf("x[%d] : ", i);
		scanf("%d", &x[i]);
	}

	insertion(x, nx);		/* 배열 x를 단순 삽입 정렬 */
	
	puts("오름차순으로 정렬했습니다.");
	for (i = 0; i < nx; i++)
		printf("x[%d] = %d\n", i, x[i]);
	
	free(x);				/* 배열을 해제 */
	
	return 0;
}

---

코드1

/*--- 단순 삽입 정렬 함수 ---*/
void insertion(int a[], int n)
{
	int i, j;
	//인덱스 0은 이미 정렬된 것으로 본다.
	for (i = 1; i < n; i++) {
		int tmp = a[i]; //현재 삽입될 숫자인 i번째 정수를 tmp로 복사해놓는다.

		//현재 정렬된 배열은 i-1까지이므로 i-1번째 부터 역순으로 조사한다.
		//i가 [0]이면 앞에 정렬된 배열이 없어서 조사할 것이 없어지므로 i는 0보다 커야 한다.
		//[i]보다 한 칸 앞에 있는 값이 [i]보다 크면 교환을 한다.
		//[i]보다 한 칸 앞에 있는 값을 오른쪽으로 이동시킨다.
		for (j = i; j > 0 && a[j - 1] > tmp; j--)
			a[j] = a[j - 1];
		
		//원래 [i]값을 왼쪽으로 한 칸 이동시킨 곳에 넣는다. 위의 for문에서 j는 --됨.
		a[j] = tmp;
	}
}

---

코드2

// 삽입 정렬

코드출처: https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html


void insertion_sort(int list[], int n){
  int i, j, key;

  // 인텍스 0은 이미 정렬된 것으로 볼 수 있다.
  for(i=1; i<n; i++){
    key = list[i]; // 현재 삽입될 숫자인 i번째 정수를 key 변수로 복사

    // 현재 정렬된 배열은 i-1까지이므로 i-1번째부터 역순으로 조사한다.
    // j 값은 음수가 아니어야 되고
    // key 값보다 정렬된 배열에 있는 값이 크면 j번째를 j+1번째로 이동
    for(j=i-1; j>=0 && list[j]>key; j--){
      list[j+1] = list[j]; // 레코드의 오른쪽으로 이동
    }

    list[j+1] = key;
  }
}

https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html

---

삽입 정렬의 특징

• 장점 :
  - 정렬을 마친 상태에 가까우면 정렬 속도가 매우 빨라진다.
  - 삽입정렬은 안정성이 있다.(stable sort)
  - 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
  - Selection Sort나 Bubble Sort과 같은 O(n^2) 알고리즘에 비교하여 상대적으로 빠르다.
• 단점 :
  - 삽입할 위치가 멀리 떨어져 있으면 이동(대입)해야 하는 횟수가 많아진다.
  - 비효율적이다.

삽입 정렬의 시간복잡도

• 최선의 경우 : O(n)
• 평균과 최악의 경우 : O(n^2)

참고)

• (내 손으로 직접 코딩하며 확인한다!) 자료구조와 함께 배우는 알고리즘 입문 - C 언어 편
• https://wonjayk.tistory.com/218?category=558920
• https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
• https://gyoogle.dev/blog/algorithm/Insertion%20Sort.html