정의
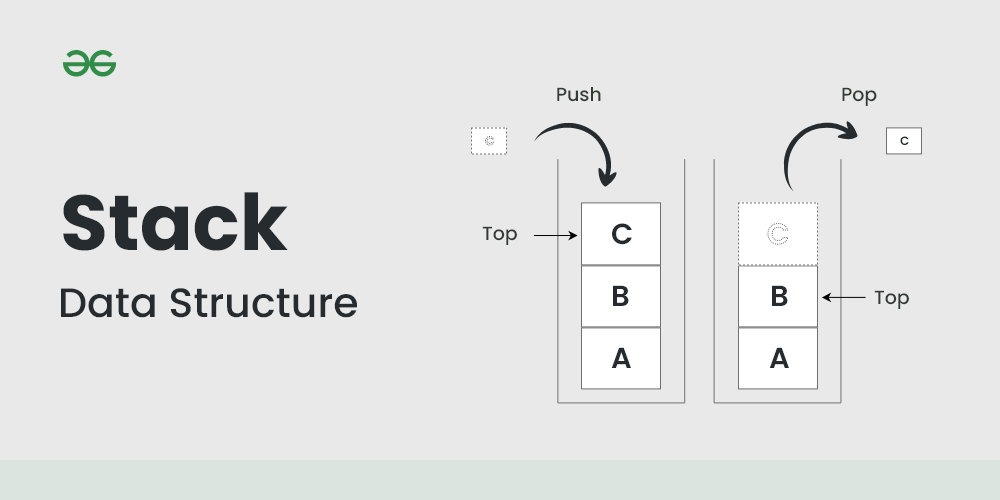
스택은 LIFO(Last In First Out) 원칙을 따르는 선형 자료구조다. 마지막에 삽입된 요소가 가장 먼저 삭제되는 구조로, 한쪽 끝(top)에서만 삽입과 삭제가 이루어진다.
기본 개념
↓ push ↑ pop
┌─────────┐
│ 5 │ ← top (최상단)
├─────────┤
│ 3 │
├─────────┤
│ 1 │
└─────────┘
주요 연산
- push: 스택의 최상단에 요소 삽입
- pop: 스택의 최상단 요소 제거 및 반환
- peek/top: 최상단 요소 조회 (제거하지 않음)
- isEmpty: 스택이 비어있는지 확인
- size: 스택의 크기 반환
시간 복잡도
| 연산 | 시간 복잡도 | 설명 |
|---|---|---|
| push | O(1) | 최상단에 삽입 |
| pop | O(1) | 최상단에서 제거 |
| peek | O(1) | 최상단 요소 조회 |
| search | O(n) | 특정 요소 찾기 |
스택의 search 시간 복잡도가 O(n)인 이유
자바스크립트에서 스택을 배열로 구현하면 본질적으로 배열과 동일하다고 생각할 수 있는데 여기서 중요한 점은 스택의 ADT(Abstract Data Type) 관점에서 생각해야 한다는 것이다.
스택에서 특정 요소를 찾으려면:
- 맨 위부터 순차적으로 확인해야 한다
- 찾는 요소가 스택의 맨 아래에 있다면 모든 요소를 확인해야 한다
- 스택의 중간 요소에 직접 접근할 수 없다 (ADT 관점에서)
// 스택에서 요소 찾기 (이론적 구현)
function searchStack(stack, target) {
let temp = [];
let found = false;
// 스택을 하나씩 pop하면서 찾기
while (!stack.isEmpty()) {
let element = stack.pop();
temp.push(element);
if (element === target) {
found = true;
break;
}
}
// 원래 스택 상태로 복원
while (temp.length > 0) {
stack.push(temp.pop());
}
return found;
}
공간 복잡도
- O(n): n개의 요소를 저장하는 공간 필요
JavaScript / TypeScript 구현
배열 기반 스택
class ArrayStack<T> {
private items: T[] = [];
// 요소 삽입
push(item: T): void {
this.items.push(item);
}
// 요소 제거 및 반환
pop(): T | undefined {
return this.items.pop();
}
// 최상단 요소 조회
peek(): T | undefined {
return this.items[this.items.length - 1];
}
// 스택이 비어있는지 확인
isEmpty(): boolean {
return this.items.length === 0;
}
// 스택 크기
size(): number {
return this.items.length;
}
// 스택 초기화
clear(): void {
this.items = [];
}
}
연결 리스트 기반 스택
class StackNode<T> {
data: T;
next: StackNode<T> | null;
constructor(data: T) {
this.data = data;
this.next = null;
}
}
class LinkedStack<T> {
private top: StackNode<T> | null = null;
private count: number = 0;
push(data: T): void {
const newNode = new StackNode(data);
newNode.next = this.top;
this.top = newNode;
this.count++;
}
pop(): T | undefined {
if (!this.top) {
return undefined;
}
const data = this.top.data;
this.top = this.top.next;
this.count--;
return data;
}
peek(): T | undefined {
return this.top?.data;
}
isEmpty(): boolean {
return this.top === null;
}
size(): number {
return this.count;
}
}
실생활 비유
접시 더미
- 접시를 쌓을 때: 맨 위에 올린다 (push)
- 접시를 꺼낼 때: 맨 위에서 가져간다 (pop)
- 중간에 있는 접시를 꺼내려면 위의 접시들을 먼저 치워야 한다
React에서의 스택 활용
모달 스택 관리
interface Modal {
id: string;
component: React.ComponentType;
props?: Record<string, any>;
}
const ModalProvider: React.FC<{ children: React.ReactNode }> = ({ children }) => {
const [modalStack, setModalStack] = useState<Modal[]>([]);
const openModal = (modal: Modal) => {
setModalStack(prev => [...prev, modal]);
};
const closeModal = () => {
setModalStack(prev => prev.slice(0, -1)); // pop과 같은 효과
};
const closeAllModals = () => {
setModalStack([]);
};
return (
<ModalContext.Provider value={{ openModal, closeModal, closeAllModals }}>
{children}
{modalStack.map((modal, index) => (
<modal.component key={modal.id} {...modal.props} />
))}
</ModalContext.Provider>
);
};
장점
- 단순한 구조: 구현이 간단하고 이해하기 쉽다
- 빠른 연산: push, pop, peek 모두 O(1) 시간
- 메모리 효율: 필요한 공간만 사용
- 자연스러운 재귀: 재귀 호출과 자연스럽게 매칭
단점
- 제한적 접근: 최상단 요소만 접근 가능
- 중간 요소 접근 불가: 특정 위치 요소에 바로 접근할 수 없다
- 검색 비효율: 특정 요소 찾기에 O(n) 시간 필요
활용 사례 정리
- 함수 호출 관리: 프로그램 실행 스택
- 표현식 계산: 중위/후위 표기법 변환, 계산기
- 구문 분석: 괄호 매칭, 컴파일러의 파싱
- 백트래킹: 미로 찾기, 퍼즐 해결
- 웹 개발: 브라우저 히스토리, Undo/Redo, 모달 관리
최적화 팁
- 크기 제한: 무한 증가 방지를 위한 최대 크기 설정
- 메모리 풀링: 자주 사용되는 경우 노드 재사용
- 배열 vs 연결리스트: 크기가 예측 가능하면 배열, 동적이면 연결리스트
- 타입 안전성: TypeScript 제네릭으로 타입 안전성 확보