[CS285] Ch4. Introduction to Reinforcement Learning 강화학습 소개

YJ·2025년 1월 17일

CS 285 DRL Deep Reinforcement Learning RL

CS 285

목록 보기

1/6

Deep Reinforcement Learning을 소개하는 Berkely CS 285 강좌의 Ch4~Ch9를 들으며 제 지식과 함께 정리해보고자 합니다. 강의 링크는 아래를 참고하세요.

https://rail.eecs.berkeley.edu/deeprlcourse/

제 나름의 지식을 많이 덧붙여 틀린 부분이 있을 수 있습니다. 발견하시면 댓글로 지적 부탁드립니다!
이해가 안되는 경우 질문도 환영입니다!

Ch4. introduction to reinforcement learning

Definitions

강화학습이란

쉽게 말해 환경(environment)과 상호작용하는 agent가 task에 맞는 올바른 행동(=reward가 높아지는 행동)을 하도록 학습시키는 방법입니다. Imitation learning(전문가의 행동을 따라하는 모방학습)과 다른 점은 정해진 정답이 없는 상태에서 reward를 통해 agent가 스스로 최적의 행동을 학습한다는 것입니다. 이는 복잡한 의사 결정 문제를 해결하기 위해 고안된 방법입니다.

용어 정의

강화학습을 공부하기 위해선 관련 용어에 익숙해져야 합니다. 관련 용어에 대해 알아보겠습니다.

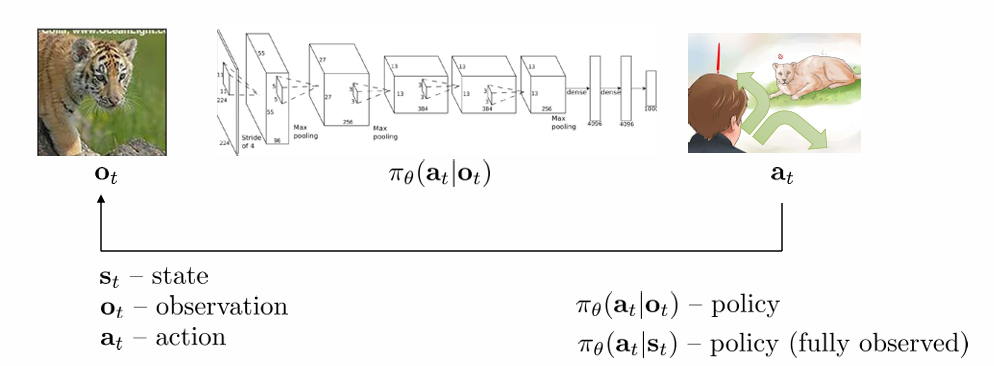
state: agent가 상호작용하는 환경을 정의하는 방식이 state입니다. 자율주행차를 만든다고 하면, 길이 오르막인지 내리막인지, 울퉁불퉁한지 평평한지, 사람이나 동물이 지나가는지 등등으로 환경을 정의할 수 있습니다. 보통 time index를 붙여 $s_t$ 로 표현합니다.

observation: 우리는 학습을 위해 state를 수학적으로 정의합니다. 그런데 agent는 sensor를 통해 환경을 인식하다 보니 한계가 존재할 수밖에 없습니다. 따라서 실제 state에 비해 observation은 한계가 있어 partially observed 될 수밖에 없습니다. 실제 구현에서는 현실을 반영하기 위해 observation이라는 용어를 사용합니다. 그러나 간단한 수학적 정의를 위해 이론에서는 state를 주로 사용하고, partially observed case를 따로 다룹니다. 보통 time index를 붙여 $o_t$ 로 표현합니다.

action: agent가 환경에 가하는 action입니다. 마찬가지로 자율주행차를 생각해보면 차의 주행 속도, 주행 방향 등을 action의 예시로 들 수 있습니다. 보통 time index를 붙여 $a_t$ 로 표현합니다.

policy: 주어진 state(또는 observation)에서 특정 action을 취할 확률 분포입니다. $\pi(a|s)$ 로 나타냅니다. 이 policy를 통해 stochastic 또는 deterministic하게 행동을 결정합니다. policy를 직접 학습하는 강화학습 방법도 있고, policy가 직접적으로 드러나지 않는 강화학습 방법도 있습니다. deep RL에서 deep learning으로 학습시키는 게 바로 이 부분입니다. 이는 후에 살펴보도록 하겠습니다.

transition function: 주어진 state에서 선택한 action을 취할 때 다음 state로 갈 확률입니다. $p = p(s'|s,a)$ 로 표현합니다.

reward: 주어진 state에서 선택한 action을 취할 때 주어지는 보상(스칼라)입니다. $r = r(s,a)$ 로 표현합니다. time index를 붙여 $r_t$ 로 표현하기도 합니다. 보상은 사용자가 정의하는 것입니다. 보상에 따라 수렴속도, 수렴 값, 심지어 수렴 여부가 달라지기도 합니다.

trajectory: 환경의 특정 state에 특정 action을 취하고, 다시 state가 변하고, 다시 action을 취하고.. 이렇게 agent가 상호작용을 반복하여 생긴 경로를 trajectory라고 합니다. $\tau = (s_1, a_1, s_2, a_2, ... s_T, a_T)$ 와 같은 방식으로 나타냅니다. reward를 넣어 표현하는 경우도 많은데, 강의의 표현 방식을 우선 따르겠습니다. 또한 initial state를 time index 0으로 표현하는 경우가 많은데, 강의와 표현을 맞추기 위해 1로 설정하겠습니다.

episode: initial state에서 환경과 상호작용을 통해 상황이 종료될 때까지를 한 epsiode라고 합니다. episode가 종료되는 시점이 정해져 있는 경우 finite horizon case, 아닌 경우를 infinite horizon case라고 합니다.

강의에서 지금 당장 설명하지 않는 것에는 return과 discount factor가 있습니다.

return, discount factor: 바둑두기, 자율주행과 같은 복잡한 의사 결정 문제에서는 당장 얻는 보상도 중요하지만 미래의 보상도 중요합니다. 당장 얻은 보상에 비해 미래의 보상에 얼마나 가중치를 둘 것인가가 discount factor입니다. $\gamma$ 로 나타냅니다. (1 이하의 값을 사용하기 때문에 discount factor라고 합니다.)
이러한 discount factor를 적용한 reward의 합을 return이라고 합니다. 시점 t에서의 return은 $G_t = \sum\gamma^{k}r_{t+k}$ 와 같이 나타냅니다. (infinite horizon 방식으로 표현하였습니다.)

MDP(Markov Decision Process)

강화학습의 가장 기본 가정은 우리가 다루는 문제가 MDP라는 가정입니다. 이는 강화학습 이론과 관련된 논문에서 무조건 가장 처음에 정의하니, 구성 요소가 무엇인지 필수적으로 알아가시면 좋습니다.

Markov Property

환경의 state $s_t$ 가 있을 때 다음 state $s_{t+1}$ 로 전이될 확률을 transition probability라고 합니다. 이 때 transition probability가 더 과거의 state와 관계 없이 직전의 state에만 영향을 받는 것을 Markov Property라고 합니다. 직전 state에만 영향을 받는다는 가정의 좋은 점은, 다음과 같이 transition probability가 간단해진다는 것입니다.

p(s_{t+1}|s_t, s_{t-1}, ..., s_0) = p(s_{t+1}|s_t)

Markov Chain

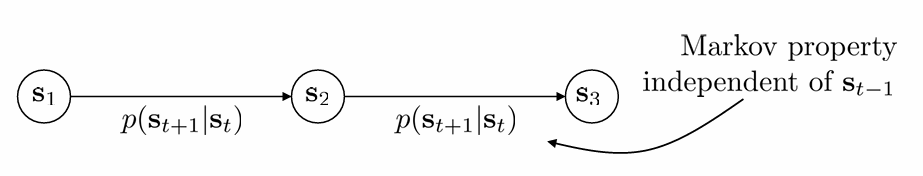
Markov Chain은 Markov Property를 가지는 discrete-time stochastic process입니다. stochastic(random) process는 시간 t에 따라 확률 분포가 변화하는 random variable을 의미합니다. discrete-time이라는 것은 실제와 달리 이 시간이 continuous 하지 않다는 것입니다. (구현에서는 dt를 fix해두고 dt마다 환경을 관측하는 방식으로 이루어집니다. discrete 하기 때문에 음수가 아닌 정수로 time index를 정의합니다.)
Markov Property를 만족하기 때문에 우리는 한 시점 $t$ 에서 다음 시점 $t+1$ 에 state $i$ 에서 state $j$ 로 넘어갈 state transition operator(여기서는 matrix)를 정의할 수 있습니다. 따라서 Markov Chain은 state space $\mathcal{S}$ 와 transition operator $\mathcal{T}$ 로 이루어졌다고 볼 수 있고, 이를 다음과 같이 표현합니다.

\mathcal{M} = \{\mathcal{S}, \mathcal{T}\}

이때 $\mathcal{T}$ 가 operator인 이유는 다음과 같이 시간 $t$ 에서 state가 $i$ 일 확률 벡터를 시간 $t+1$ 에서 state가 $j$ 일 확률 벡터로 선형 변환해주는, operator의 역할을 하기 때문입니다.

\mathcal{T}_{i,j} = p(s_{t+1}=j|s_t=i)

\mu_{t,i} = p(s_t=i)

\mathcal{T}_{i,j}\mu_{t,i}=\mu_{t+1,j}

예시를 통해 이해하면 쉬운데, 이는 kreyszig 공업수학 10판 7.2절의 예제를 통해 설명하도록 하겠습니다.

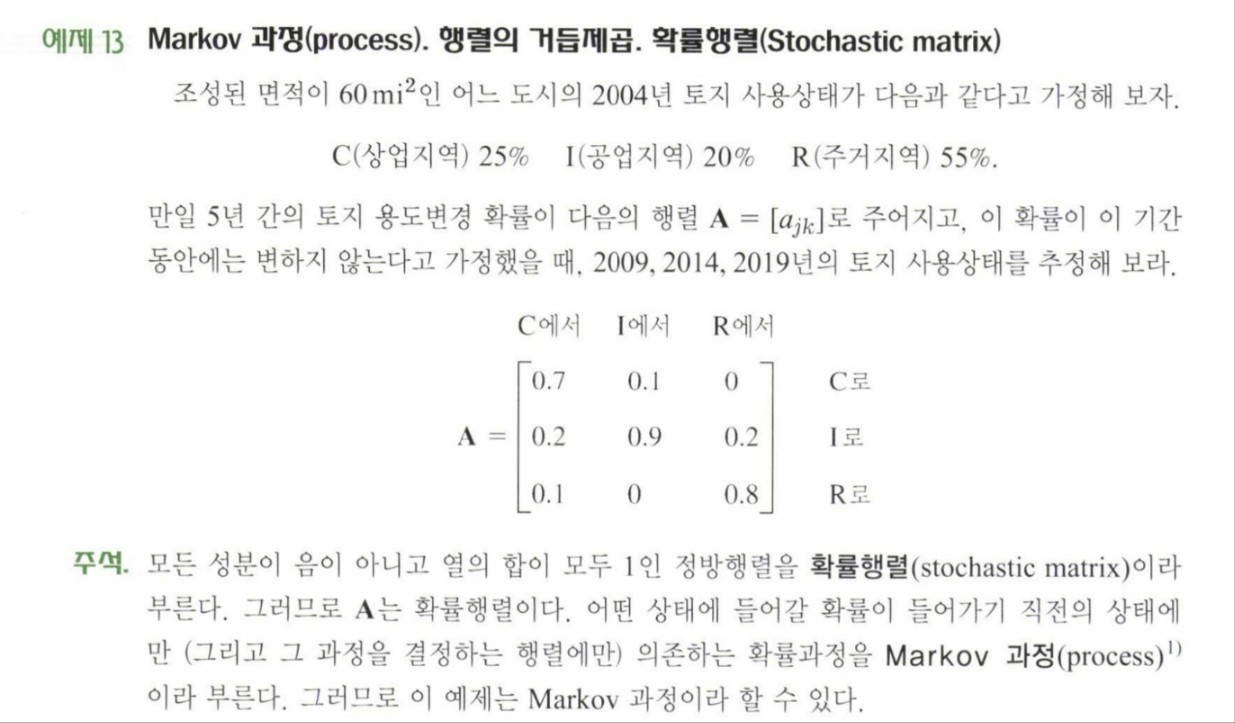
어떤 년도의 토지 사용 비율은 5년전의 토지 사용 비율에만 영향을 받고, 한 용도로 사용되던 토지가 다른 용도로 사용될 확률은 위와 같이 transition matrix로 주어집니다. 그렇다면 2014년의 토지 사용 상태는 다음과 같이 행렬 곱으로 구할 수 있습니다.

x_{04} = \begin{pmatrix} 0.25\\ 0.20\\ 0.55 \end{pmatrix}

x_{09} = Ax_{04} = \begin{pmatrix} 0.7 & 0.1 & 0.0\\ 0.2 & 0.9 & 0.2\\ 0.1 & 0.0 & 0.8 \end{pmatrix} \begin{pmatrix} 0.25\\ 0.20\\ 0.55 \end{pmatrix} = \begin{pmatrix} 0.195\\ 0.340\\ 0.465 \end{pmatrix}

따라서 2009년에 상업지역으로 19.5%, 공업지역으로 34%, 주거지역으로 46.5%의 토지가 사용된다고 볼 수 있습니다.

Markov Decision Process

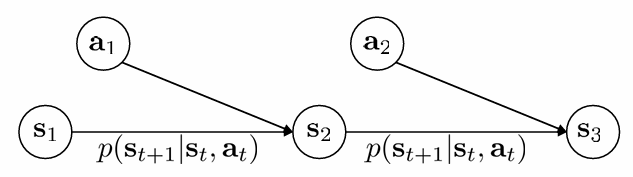
Markov Chain만으로는 강화학습을 설명할 수 없습니다. action이 없기 때문입니다. action이라는 decision을 통해 환경과 상호작용하는 Markov Chain을 MDP라고 합니다. 이 때 MDP의 구성요소는 action space $\mathcal{A}$ 와 reward function $r$ 을 포함하여 다음과 같이 표현합니다.

\mathcal{M} = \{\mathcal{S}, \mathcal{T}, \mathcal{A}, r\}

이제 transition에 action도 함께 관여하기 때문에, transition operator는 tensor가 되어 다음과 같이 나타낼 수 있습니다.

\mathcal{T}_{i,j,k} = p(s_{t+1}=k|s_t=i,a_t=j)

\mu_{t,i} = p(s_t=i)

\xi_{t,j} = p(a_t=j)

\mathcal{T}_{i,j,k}\mu_{t,i}\xi_{t,j}=\mu_{t+1,k}

RL 이론과 관련된 논문에서 아래와 같이 MDP notation을 정의하고 시작하는 경우가 많습니다. 참고하세요
(논문은 soft actor-critic입니다. https://arxiv.org/abs/1801.01290)

Partially Observed MDP

partially observed case의 경우에는 observation space $\mathcal{O}$ 와 emission probability ${\varepsilon}=p(o_t|s_t)$ 을 포함하여 다음과 같이 작성합니다. 그렇게 중요하게 다루진 않지만 짚고 넘어갑시다.

\mathcal{M} = \{\mathcal{S}, \mathcal{T}, \mathcal{A}, \mathcal{O}, \varepsilon, r\}

Goal of Reinfocement Learning

probability of trajectory

Markov 가정에 의해 앞서 정의한 trajectory의 probability를 작성해보면 다음과 같습니다.

p_\theta(\tau) = p_\theta(s_1, a_1, s_2, a_2, ... s_T, a_T) = p(s_1)\displaystyle\prod_{t=1}^{T}{\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)}

복잡해 보이지만, $\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)$ 은 한 state에서 action을 고르고, 그 state에서 action을 골랐기 때문에 이루어지는 transition의 확률입니다. 첫 state부터 이러한 transition이 T까지 일어난다는 의미가 됩니다.

objective function

우리가 원하는 것은 agnet가 보상이 최대화되는 방향으로 policy를 학습하는 것입니다. policy는 stochastic하기 때문에, 같은 policy를 사용하더라도 매번 trajectory가 달라지겠죠. 우리는 가능한 모든 trajectory에 대해 보상이 높았으면 좋겠습니다. 따라서 다음과 같이 reward의 합인 return(이 때 discount factor = 1로 우선 시작합니다)의 기댓값을 최대화하는 게 강화학습의 goal이며, 이 기댓값이 objective function이 됩니다.

E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t}{r(s_t,a_t)}\right]

다음 강의부터 본격적으로 배우는 policy gradient의 경우에는 policy를 $\theta$ 로 매개화하게 됩니다. DRL에서는 결국 policy로 neural net을 사용한다고 보시면 됩니다. 그렇다면 이 neural net의 weight가 학습 대상이 되고, $\theta$ 는 다음과 같이 구할 수 있습니다.

\theta^*=\argmax_\theta E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t}{r(s_t,a_t)}\right]

이 때 finite horizon case의 경우 expectation의 linearity를 이용하여 식을 다음과 같이 전개할 수 있습니다.

=\argmax_\theta \displaystyle\sum_{t=1}^{T}{E_{\tau\sim p_\theta(\tau)}\left[r(s_t,a_t)\right]}

infinite horizon case의 경우에는 linearity를 함부로 적용할 수 없는데요( $T \rightarrow \infin$ 이기 때문), 이런 경우 stationary distribution을 가정합니다. stationary distribution이란 transition이 계속해서 반복되다 보면 state distribution(특정 상태에 머무를 확률)이 결국 고정된다는 것입니다. 이는 결국 다음과 같은 식의 성립을 이야기하는 것이므로 transition matrix가 1인 eigenvalue를 갖는다는 가정입니다.

\mu =\mathcal{T}\mu

(\mathcal{T}-I)\mu=0

stationary distribution은 앞서 살펴본 예제에서도 성립합니다. eigenvalue를 1로 두면 eigenvector를 구할 수 있고, 이는 곧 $T \rightarrow \infin$ 에서의 state distribution이 됩니다. 계산 과정은 생략하겠습니다.
이 statinary distribution 가정에 의해 $T \rightarrow \infin$ 에서 다음 식이 성립합니다. objective를 T로 나누어준 것은 수렴성을 보장하기 위해서입니다.

\theta^*=\argmax_\theta \frac{1}{T} \displaystyle\sum_{t=1}^{T}{E_{\tau\sim p_\theta(\tau)}\left[r(s_t,a_t)\right]} \rightarrow E_{(s,a)\sim p_\theta(s,a)}\left[r(s,a)\right]

즉 $T \rightarrow \infin$ 이니 (s,a)의 확률이 일정해지고 이 확률분포에 의한 각 time에서 보상의 평균은 결국 한 time에서 보상의 기댓값이 된다는 것이죠.

why expectation?

강화학습에서는 이렇듯 대부분의 경우 expectation을 수학적으로 다루는데요. 그 이유는 smooth하게 만들기(미분 가능하게 만들기라고 보시면 됩니다) 위해서입니다.

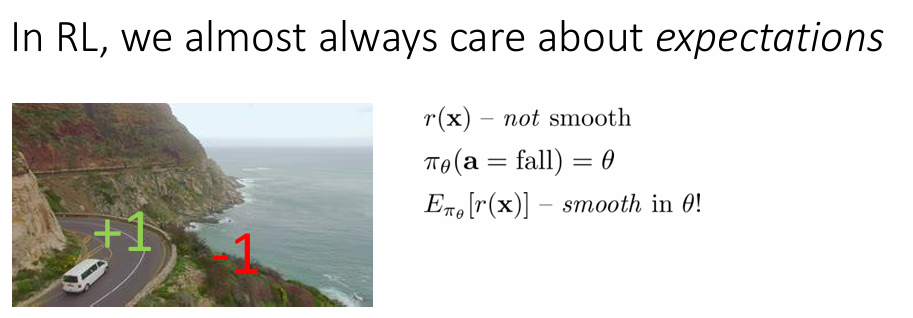
강의의 예시입니다. 우리가 만약 절벽 옆을 지나갈 때, 절벽을 통과하면 보상이 1, 떨어지면 -1이라고 하겠습니다. station과 action space에서 reward function은 smooth하지 않습니다. (1또는 -1이니, 불연속인 공간이 생긴다고 보시면 됩니다.)
이 때 policy를, action이 fall일 확률을 theta로 매개화한다면, reward의 expectation은 다음과 같이 $\theta$ 에 대해 smooth해지는 것을 확인할 수 있습니다. 이와 같은 성질 때문에 expectation을 사용합니다.

E_{\pi_\theta}[r(x)]=1\times(1-\theta)-1\times\theta=1-2\theta

Algorithms

anatomy of a reinforcement learning algorithm

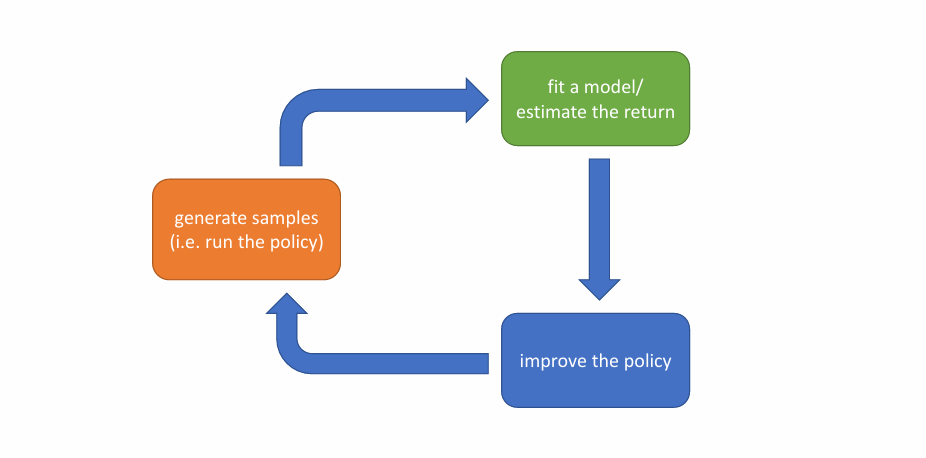
모든 RL 알고리즘은 이와 같이 세 단계의 반복으로 이해할 수 있습니다.

generate samples: 학습을 하려면 우선 sample이 있어야겠죠. 환경과 상호작용을 하는 단계입니다.
fit a model / estimate the return: improve를 위해 필요한 계산을 하는 단계입니다. return의 기댓값을 알아야 하기 때문에 return을 추정하는 단계도 여기에 들어가 있습니다.
improve the policy: 계산을 바탕으로 policy를 improve 합니다.

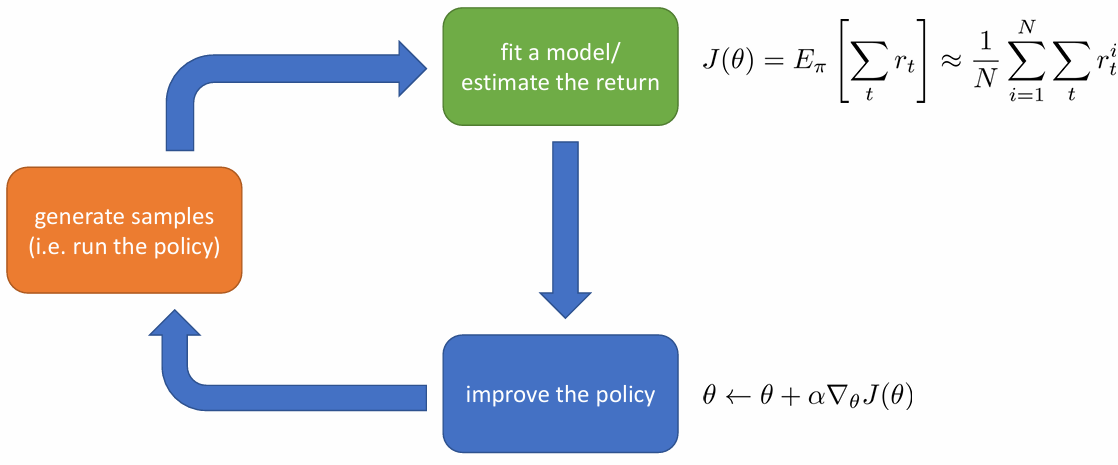
강의의 예시입니다. 단순히 return의 기댓값을 sample을 많이 뽑아 평균하는 방식으로 계산하고, parameter $\theta$ 를 objective function에 대한 gradient ascent(objective function인 expectation of return을 최대화해야 하므로)로 update하는 방식입니다. objective function의 gradient는 다음 강에서 본격적으로 살펴볼 예정입니다.

which part is expensive?

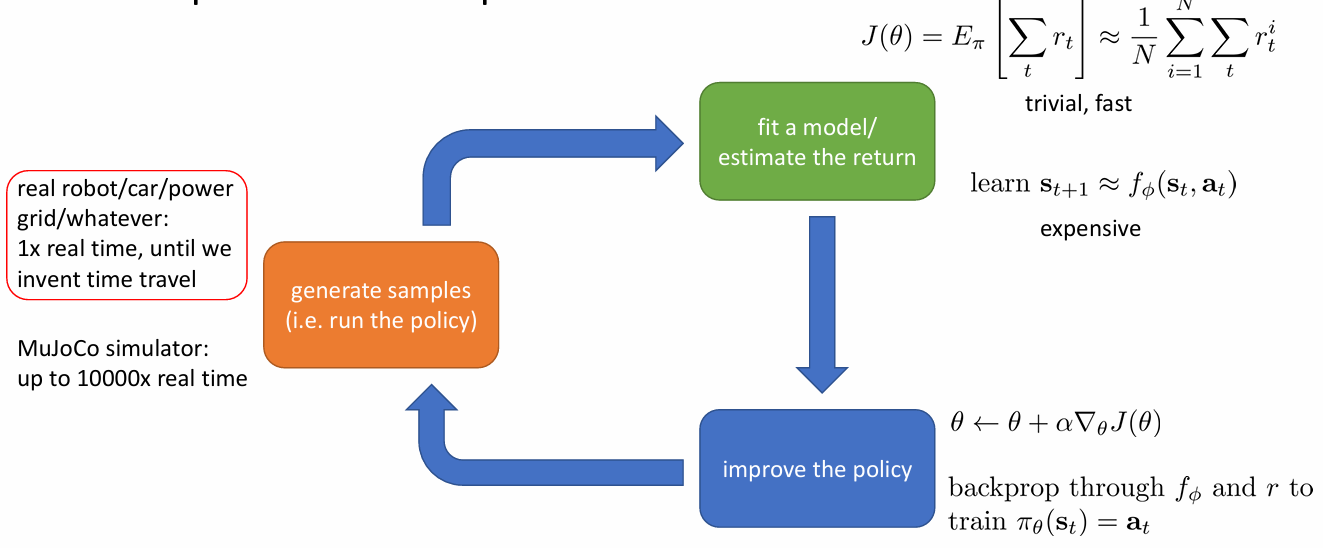
셋 중 어떤 부분이 비용이 많이 드는지는 환경에 따라 다릅니다. 시뮬레이션을 할 수 있다면 sample generation은 비교적 쌉니다. 두 번째 단계에서는 neural net을 학습하는 것 보다는 단순히 구해진 return을 평균하는 게 훨씬 빠르겠죠. policy를 improve하는 부분도 알고리즘에 따라 다릅니다.

Value Functions

강화학습에서 policy가 직접적으로 드러나지 않는 알고리즘들이 있다고 했었죠. 그 알고리즘들은 value function을 이용합니다. value function은 Q-function(state & action value function)과 Value function(state value function)으로 나뉩니다.

Definitions

Q function: time step t의 state $s_t$ 에서 action $a_t$ 를 취했을 때, 앞으로 얻게 될(time step T까지) reward의 합(return)의 기댓값입니다.

Q^\pi(s_t,a_t) = \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t,a_t]

reward function은 정해져있기 때문에, time step t에서의 reward는 정해진 값이고, t+1부터는 transition probability와 policy에 따라서 확률적으로 분포합니다. 따라서 앞으로의 return은 예측해야하는 값이고, 이를 예측하기 위해 기댓값을 사용하는 게 적절하겠죠.

Value function: time step t에서 state가 $s_t$ 일 때 앞으로 얻게 될 return의 기댓값입니다.

V^\pi(s_t) = \sum_{t'=t}^{T} E_{\pi_\theta}[r(s_{t'},a_{t'})|s_t]

정의에 의해 Value function은 Q function의 기댓값이 됩니다. trajectory의 time step t에서 취할 수 있는 action의 분포는 policy를 따르기 때문에, 다음과 같이 나타낼 수 있습니다.

V^\pi(s_t) = E_{a_t \sim \pi_\theta(a_t|s_t)}[Q^\pi(s_t,a_t)]

Usage (1): objective function

Q-function과 Value function을 정의해서 좋은 점은 objetive function을 좀 더 간단히 나타낼 수 있다는 점입니다. 앞서 finite horizon case에서 RL의 objective function이 다음과 같음을 설명한 바 있습니다.

E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t=1}^{T}{r(s_t,a_t)}\right]

이를 state와 action을 쪼개 매 step에 대해 나타내면 다음과 같습니다.

E_{s_1 \sim p(s_1)}[E_{a_1 \sim \pi(a_1|s_1)}[r(s_1, a_1) +E_{s_2 \sim p(s_2|s_1,a_1)}[E_{a_2 \sim \pi(a_2|s_2)}[r(s_2,a_2)+...|s_2]|s_1,a_1]|s_1]]

조금 복잡해보이지만, s_1이 p를 따르고, action은 policy를 따르고, 그 다음 state는 transition probability를 따르고...를 풀어서 설명한 것입니다. 이 때, Q function을 이용해 이를 나타내면 다음과 같습니다.

E_{s_1 \sim p(s_1)}[E_{a_1 \sim \pi(a_1|s_1)}[Q(s_1,a_1)|s_1]]

앞서 살펴본 Q function과 Value function의 정의에 의해 최종적으로 다음과 같이 나타낼 수 있습니다.

E_{s_1 \sim p(s_1)}[V(s_1)]

즉 RL의 objective function은 initial state value function의 기대값이 됩니다.

Usage (2): update policy

policy를 update 하는 데에 value function을 이용할 수 있습니다.

$a = \argmax_a Q(s,a)$ 인 action을 $\pi'(a|s)=1$ 로 만들기

다시 말해 특정 state에서 가장 높은 return 기댓값을 갖는 행동만 취하자는 뜻입니다. 굉장히 hard한 방식이죠. 이는 policy가 무엇인지와는 크게 관계가 없습니다. 다시말해 explicit한 policy를 가질 필요 없이, argmax를 취하는 방식으로 행동을 결정할 수 있습니다. 이는 value based method의 핵심 아이디어입니다.

good action a가 취해질 확률을 높이는 방식으로 policy update

앞서 argmax를 취하는 방식으로 hard하게 action을 결정하는 방식을 취했다면, 지금은 좋은 action을 뽑을 확률 $\pi(a|s)$ 를 높이는 방식으로 gradient를 구합니다. 이는 policy gradient method의 핵심 아이디어입니다.
그렇다면 좋은 action이란 무엇일까요? 정의에 의해 같은 state에 대해 Q-function 값이 Value function값보다 크다면, 평균보다 return이 큰 action이라고 볼 수 있습니다. 따라서 이러한 action을 좋은 action이라고 할 수 있고, 이를 위해 $Q-V$ 를 따로 Advantage function이라고 정의합니다. 더 자세한 이야기는 다음 강에서 살펴보겠습니다.

Types of Algorithms

RL의 알고리즘을 개괄적으로 소개하도록 하겠습니다. 자세한 내용은 앞으로의 포스팅을 통해 살펴볼 예정입니다.

Model-based algorithms

환경이 상호작용에 의해 변화하는 규칙을 알고 있다 = transition function을 알고 있다는 가정 하에 행동을 최적화하는 방법입니다. 저는 model-based algorithm까지는 다루지 않을 것이기 때문에, transition function을 예측하는 것이 model-based algorithm이다 정도만 짚고 넘어가도록 하겠습니다.

Policy Gradients

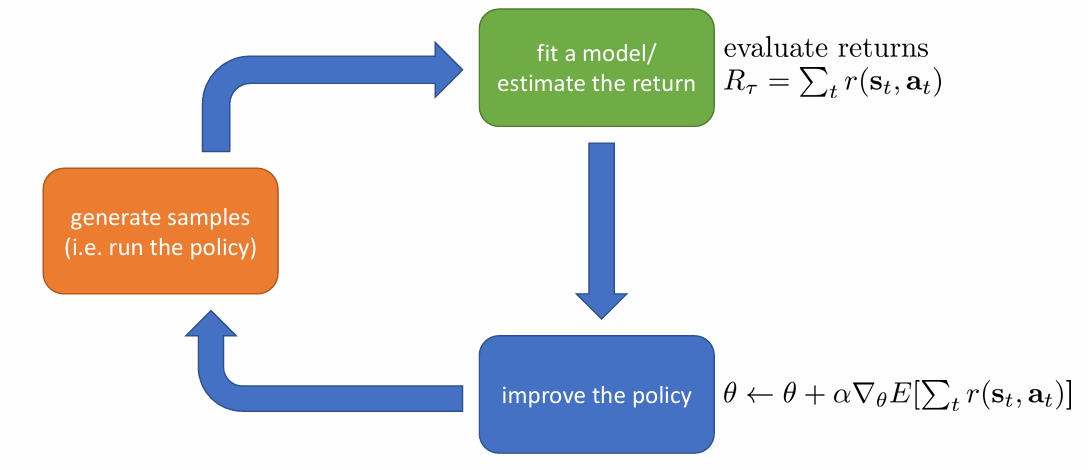
objective function의 direct한 gradient를 구해서 이를 gradient ascent 하는 방식으로 policy를 update하는 방법입니다. 앞서 살펴보았듯이 좋은 action을 택할 확률을 높이는 방향으로 policy가 update되게 됩니다.

Value Based

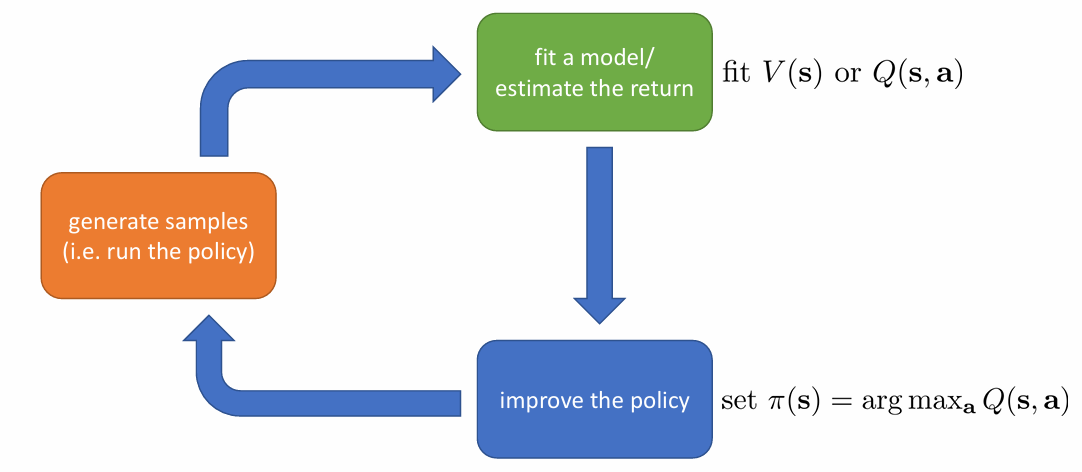
value function을 구해 argmax를 취하는 방식으로, 직접적인 policy를 나타내지 않는 방법입니다.

Actor-Critic

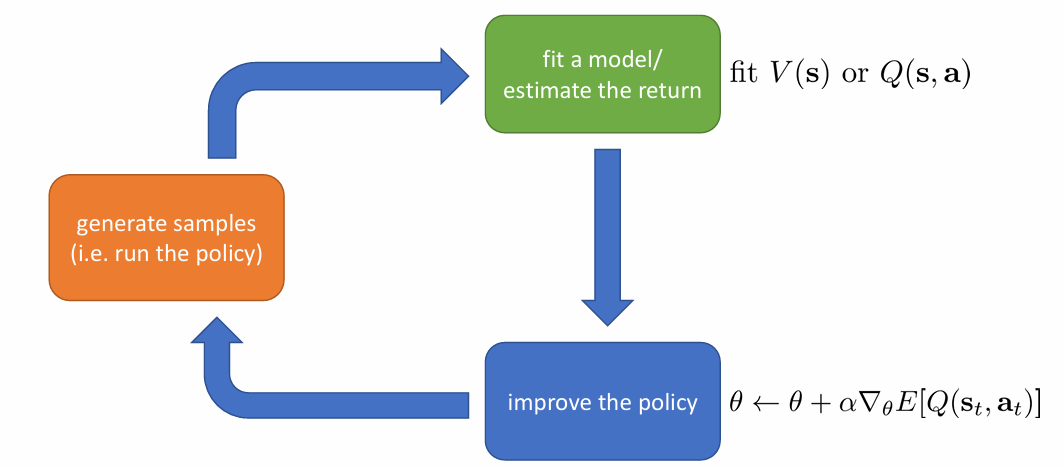
두 방법을 합친 방법으로 value function을 estimate하여 policy를 update하는 방식입니다.

Tradeoffs between Algorithms

그렇다면 왜 이렇게 많은 알고리즘이 존재하는 것일까요? 그 이유는 바로 알고리즘이 각각의 특성을 가져 문제 상황에 따라 적절한 알고리즘이 달라지기 때문입니다.

sample efficiency

sample efficiency란 적절한 학습을 하는 데 필요한 샘플의 양을 의미합니다. sample이 많이 필요하다면 효율적이라고 할 수 없겠죠. 이와 관련된 알고리즘의 특성이 있습니다. on-policy와 off-policy입니다.

on-policy: 그 policy로 얻은 sample만 학습에 사용할 수 있는 알고리즘입니다.
off-policy: 다른 policy로 얻은 sample도 학습에 사용할 수 있는 알고리즘입니다.

당연히 off-policy가 sample 효율성이 좋을 것입니다. 일단 sample을 조금 더 쉽게 얻을 수 있습니다. off-policy 내에서도 더 적은 sample이 필요한 알고리즘들이 존재합니다.

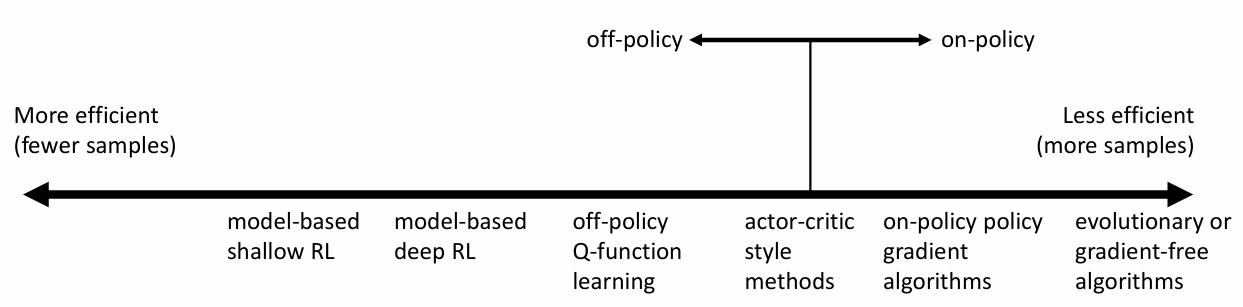
그러나 우리가 항상 off-policy 알고리즘만을 사용하는 것은 아닙니다. sample 효율성이 낮더라도 시뮬레이션이 가능하다면 충분히 많은 sample을 얻을 수 있고, 그래서 다른 장점이 있는(덜 복잡하다던가, 더 안정하다던가) on-policy 알고리즘을 사용하게 되는 경우도 많습니다.

stability and ease of use

문제 상황에 따라 특정 알고리즘은 수렴하지 않을 수도 있습니다. 이는 알고리즘을 이용할 때 가장 먼저 고려해야할 부분입니다. 열심히 학습을 했는데 수렴하지 않는다면 아무 의미 없는 학습이 되겠죠. 따라서 수렴하는가? 무엇으로 수렴하는가? 항상 수렴하는가?와 같은 질문이 RL에서는 문제가 될 수 있습니다. 수렴성에 관해서는 알고리즘들을 배우면서 더 깊게 살펴보도록 하겠습니다.

assumption

알고리즘마다 전제가 다르기 때문에, 특정 상황에서 사용할 수 있는 알고리즘이 달라집니다. 다음과 같은 가정들이 자주 등장합니다.

full observability: state를 fully observable하다고 가정하는 알고리즘입니다. value function을 fitting하는 method에서 주로 사용하는 가정입니다.
episodic learning: 우리가 상호작용하는 환경이 에피소드로 이루어져있다, 즉 끝이 있다고 보는 가정입니다. pure policy gradients에서 자주 가정합니다.
continuity or smoothness: 우리가 사용하는 수학적인 장치들로 인해 사용되는 가정입니다. continuous value function learning method에서 주로 사용합니다.

이로서 ch4에 대한 포스팅이 끝났습니다. 예시는 강의를 참고하시길 추천드립니다. 틀린 부분이나 이해가 안된 부분이 있다면 댓글 주세요!

CS285 website: https://rail.eecs.berkeley.edu/deeprlcourse/

다음 포스트

[CS285] Ch4. Introduction to Reinforcement Learning 강화학습 소개

CS 285

Ch4. introduction to reinforcement learning