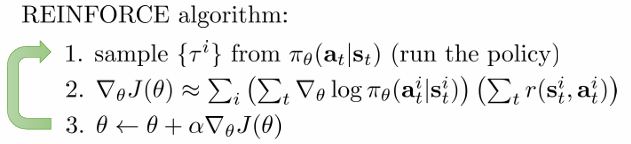[CS285] Ch5. Policy Gradient

YJ·2025년 1월 20일

CS 285 DRL Deep Reinforcement Learning RL

CS 285

목록 보기

2/6

Deep Reinforcement Learning을 소개하는 Berkely CS 285 강좌의 Ch4~Ch9를 들으며 제 지식과 함께 정리해보고자 합니다. 강의 링크는 아래를 참고하세요.

https://rail.eecs.berkeley.edu/deeprlcourse/

제 나름의 지식을 많이 덧붙여 틀린 부분이 있을 수 있습니다. 발견하시면 댓글로 지적 부탁드립니다!
이해가 안되는 경우 질문도 환영입니다!

Ch5. Policy Gradient

Direct policy differentiation

objective function of RL

ch4에서 RL의 objective function은 return의 기댓값이라고 언급한 바 있습니다. 수식으로 살펴보면 다음과 같이 objective function을 최대화하는 parameter를 찾는 게 RL의 학습이 됩니다.

\theta^*=\argmax_\theta E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t}{r(s_t,a_t)}\right]

finite horizon case의 경우 objective function을 다음과 같이 전개할 수 있고

\theta^*= \argmax_\theta \displaystyle\sum_{t=1}^{T}{E_{\tau\sim p_\theta(\tau)}\left[r(s_t,a_t)\right]}

infinite horizon case의 경우 statinary distribution 가정을 하면 다음과 같이 정리할 수 있다고 언급한 바 있습니다.

\theta^*= \argmax_\theta E_{(s,a)\sim p_\theta(s,a)}\left[r(s,a)\right]

evaluating the objective

objective function은 결국 return의 기댓값인데요, 기댓값을 계산하기 위해서는 trajectory의 확률 분포와 각 경우의 return 값을 알아야합니다. 그러나 대부분의 환경에서 이를 아는 것은 굉장히 어렵습니다. (이것이 model-free 알고리즘이고, 제 포스팅에서 다룰 것은 전부 model-free algorithm입니다.) 따라서 우리는 환경과 많이 부딪혀보면서(=sampling) 얻은 샘플로 return의 기댓값을 추정해야만 합니다.

가장 간단한 방법은 N번의 시행을 통해 얻은 return을 평균내는 방식입니다. (이를 Monte Carlo Estimation이라고 합니다.)이는 다음과 같은 식으로 나타낼 수 있습니다

J(\theta) = E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t}{r(s_t,a_t)}\right] \approx \frac{1}{N}\sum_{i}\sum_{t}r(s_{i,t}, a_{i,t})

i는 sample에 대한 index입니다.

direct policy differentiation

같은 방식을 gradient에 대해서도 사용할 수 있는데요, 그러면 우선 gradient를 구하는 식을 알아야만 합니다. objective function의 gradient 값을 알아보도록 하겠습니다. objective function은 다음과 같습니다.

J(\theta) = E_{\tau\sim p_\theta(\tau)}\left[\displaystyle\sum_{t}{r(s_t,a_t)}\right]

objective function을 trajectory $\tau$ 에 대해 간단히 나타낸 뒤 기댓값의 정의에 의해 식으로 나타내면 다음과 같습니다.

J(\theta)= E_{\tau\sim p_\theta(\tau)}[r(\tau)] = \int p_\theta(\tau)r(\tau)d \tau

$\theta$ 에 대한 gradient를 취하면 gradient를 integral 안으로 넣을 수 있습니다.

\nabla_\theta J(\theta)= \nabla_\theta \int p_\theta(\tau)r(\tau)d \tau = \int \nabla_\theta p_\theta(\tau)r(\tau)d \tau

다음과 같은 trick을 이용하면 gradient를 간단히 정리할 수 있습니다.

p_\theta(\tau) \nabla_\theta \log{p_\theta(\tau)} = p_\theta(\tau) \frac{\nabla_\theta p_\theta(\tau)}{p_\theta(\tau)} = \nabla_\theta p_\theta(\tau)

\nabla_\theta J(\theta)= \int \nabla_\theta p_\theta(\tau)r(\tau)d \tau = \int p_\theta(\tau) \nabla_\theta \log{ p_\theta(\tau)}r(\tau)d \tau = E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}r(\tau)]

gradient를 마찬가지로 기댓값 기호를 이용해 나타낼 수 있게 되었습니다.

그렇다면 objective function을 N번의 시행을 통해 얻은 return 값의 평균으로 추정했던 것과 마찬가지로, N번의 시행을 통해 얻은 괄호 안의 값의 평균으로 추정해볼 수 있을 겁니다. 그 전에 괄호 안의 식을 좀 더 풀어보아야 합니다.

지난 포스팅에서 MDP 성질을 가지는 trajectory의 probability를 다음과 같은 식을 통해 정리한 바 있습니다.

p_\theta(\tau) = p_\theta(s_1, a_1, s_2, a_2, ... s_T, a_T) = p(s_1)\displaystyle\prod_{t=1}^{T}{\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)}

이는 결국 state $s_t$ 에서 policy를 통해 action $a_t$ 를 뽑고 transition probability에 의해 다음 state $s_{t+1}$ 을 뽑는 과정의 반복이었습니다. 이 식에 로그를 씌워주면 다음과 같이 정리할 수 있습니다.

\log{p_\theta(\tau)} = \log{p(s_1)} + \displaystyle\sum_{t=1}^{T}{\log{\pi_\theta(a_t|s_t)}}+\displaystyle\sum_{t=1}^{T}{\log{p(s_{t+1}|s_t,a_t)}}

여기에 $\theta$ 에 대한 gradient를 취해주면 다음과 같이 가운데 항만 남게 됩니다. 이는 policy만이 $\theta$ 에 대한 식이고 나머지는 $\theta$ 와 관계 없기 때문입니다.

\nabla_\theta \log{p_\theta(\tau)} = \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_t|s_t)}}

따라서 이 식을 이용하여 objective function의 gradient를 나타내보면 다음과 같습니다.

\nabla_\theta J(\theta) = E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}r(\tau)] = E_{\tau\sim p_\theta(\tau)}\left[\left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_t|s_t)}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_t,a_t)} \right) \right]

그렇다면 이제 이 값을 N번 계산해 얻은 평균으로 다음과 같이 gradient를 추정할 수 있습니다.

\nabla_\theta J(\theta) = E_{\tau\sim p_\theta(\tau)}\left[\left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_t|s_t)}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_t,a_t)} \right) \right] \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_{i,t},a_{i,t})} \right)

그러면 이렇게 얻은 gradient로 목적함수를 최대화 하는 방향으로 $\theta$ 를 update하는 gradient ascent를 쓰게 됩니다.

\theta \leftarrow \theta + \nabla_\theta J(\theta)

이 때 보상함수는 우리가 직접 설정하거나 환경에서 주어지는 값이고, DRL에서 policy는 neural network로 주어지기 때문에 backpropagation을 통해 gradient를 구하기만 하면 됩니다. pytorch나 tensorflow같은 라이브러리들이 gradient를 자동으로 계산해주기 때문에, 우리는 단순히 N번의 시행을 통해 gradient를 구할 수 있게 되는 것입니다.

REINFORCE 알고리즘

여기서 policy gradient의 가장 기본이 되는 REINFORCE 알고리즘이 나오게 됩니다. 알고리즘은 다음과 같습니다. 방금까지 설명한 내용이므로 알고리즘에 대해서는 더 설명하지 않겠습니다.

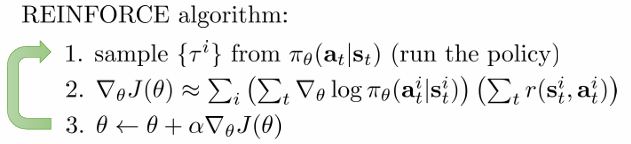
Understanding Policy Gradients

policy gradient 식의 의미를 maximum likelihood method와 비교해보면 정성적 의미를 파악하기가 쉬워집니다. 우선 앞서 구한 RL의 objective function 의 gradient는 다음과 같았습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_{i,t},a_{i,t})} \right)

Maiximum likelihood method의 objective function은 다음과 같습니다. likelihood란 데이터가 특정 분포에서 만들어졌을 확률을 의미합니다. state에 대한 최적의 action이 주어진 상황에서 policy $\pi$ 를 $\theta$ 로 매개화 했을 때, 그 policy에서 state가 주어졌을 때 그 action을 선택할 확률을 높이는 방식으로, 즉 likelihood를 높이는 방식로 $\theta$ 를 update합니다.

\nabla_\theta J_{ML}(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}}\right)

(maximum likelihood에 관해서는 다음 글을 참고하시면 좋을 거 같습니다. https://process-mining.tistory.com/93)

두 gradient의 공통점이 보이시나요? policy gradient의 return 항을 제외하고는 식이 동일합니다. ML 방법에서는 state에 대한 최적의 action이 주어져있기 때문에 그 state에서 그 action을 선택할 확률을 높이기만 하면 됩니다. 그러나 policy gradient에서는 state에 대한 action이 현재 policy에 의해 생성되고 그 action이 얼마나 좋은지 나쁜지가 reward로 주어질 뿐입니다. 따라서, reward에 따라 reward가 큰 action은 증가시키고 reward가 작은 쪽은 감소시키는 방향으로 $\theta$ 를 update하게 된다는 것입니다. 이것이 return 항의 유무 차이가 발생하는 이유입니다.

강의에는 gaussian policy의 예시가 나오긴 하는데, 직관적인 이해가 중요한 부분이라고 생각하기 때문에 추후에 추가하도록 하겠습니다.

Partial Observability

partial observability case에 대해서도 딱히 변화 없이 식을 사용할 수 있습니다. 이 경우 policy는 어차피 observe에 의해 결정되는 것이고, reward는 state와 action에 대한 함수니 식을 이렇게 쓰는 것 뿐입니다.

Reducing Variance

high variance

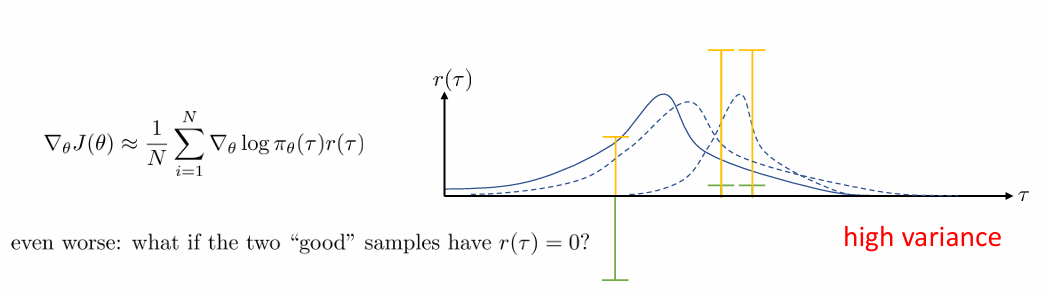
policy gradient의 큰 문제가 있는데요, 바로 high variance입니다. 위의 그림의 예시를 통해 살펴보겠습니다. Return이 초록색과 같이 주어지는 경우, policy gradient를 이용하여 update하면 probability distribution은 return이 음수인 경우를 아주 줄이고, return이 양수인 경우를 아주 늘리면서 급격하게 변화하게 됩니다. (맨 오른쪽 곡선) Return이 노란색처럼 주어지는 경우에는 probability distribution이 초록색에 비해서는 덜 급격하게 변하게 됩니다.(가운데 곡선) 만약 오른쪽 두 경우의 Return이 0으로 주어진다면 어떨까요? 왼쪽 trajectory의 확률만 급격하게 줄이는 쪽으로 변화하게 될 것입니다. 즉, sample이 어떤 trajectory고 보상이 어떻게 주어지느냐에 따라 policy가 천차만별로 update 된다는 것입니다.

우리는 gradient 예측에 finite한 size의 sample을 사용하기 때문에 이렇듯 gradient는 일반화되지 못하고 샘플에 따라 급격하게 변화하게 됩니다. 즉, 올바른 예측값이 되지 못한다는 것이죠. 이러한 high variance를 줄여야 알고리즘이 잘 작동할 것입니다. 우리는 sample에 overfitting된 policy를 얻고 싶은 게 아니라 어떤 상황에서도 잘 작동하는 policy를 만들고 싶기 때문입니다. 이를 위한 두 가지 방법을 소개하도록 하겠습니다.

reducing variance(1): causality

앞서 정리한 objective의 gradient는 다음과 같습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_{i,t},a_{i,t})} \right)

여기서 괄호가 쳐져있는 두 항을 다음과 같이 전개해볼 수 있습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=1}^{T}{r(s_{i,t'},a_{i,t'})} \right)

즉, 한 시행에서의 gradient는 매번 timestep에서 policy의 gradient에 return을 곱해준 값을 더한 게 됩니다. 그런데 time step = t에서의 action에 이전의 return들은 아무 의미를 갖지 못합니다. 현재의 action은 미래의 return에만 영향을 주게 되니까요. 이러한 성질을 causality라고 하며, 따라서 위 식을 다음과 같이 정리해볼 수 있습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=t}^{T}{r(s_{i,t'},a_{i,t'})} \right)

매 time step에서 gradient에 앞으로의 return을 곱한 값을 모두 더하게 되는 것이죠. 이러한 return을 "reward to go"라고 이야기하며, $\hat{Q}_{i,t}$ 로 표기합니다.

Causality를 이용하게 되면서 gradient에 곱해주는 return값 자체가 작아지게 됩니다. 따라서 우리가 예측한 gradient 값도 줄어들테고, 그렇게 high variance를 낮추는 방식이 causality를 이용한 방식입니다.

reducing variance(2): baseline

Variance를 낮추기 위해서 causality보다 자주 쓰이는 방식이 baseline입니다. Baseline은 즉 return을 그냥 곱해주지 않고 다음과 같이 baseline b를 빼준 값을 곱해서 전체 variance를 낮추는 방식입니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \left(\displaystyle\sum_{t'=1}^{T}{r(s_{i,t'},a_{i,t'})} - b \right)

Baseline에는 다음과 같이 return의 평균을 많이 사용합니다. 이 baseline을 쓰게 되면 평균보다 return이 높은 행동은 더 많이, 평균보다 return이 낮은 행동은 더 적게 하도록 policy가 update 될 것입니다.

b = \frac{1}{N} \displaystyle\sum_{i=1}^{N}{\displaystyle\sum_{t'=1}^{T} r(s_{i,t'},a_{i,t'})}

말은 되는 것 같은데, 이렇게 함부로 baseline을 빼주어도 되는 것일까요? 결론적으로는 가능합니다. 다음과 같이 gradient에 baseline을 곱한 기댓값은 0이라서, 결국 원래 식 자체에는 변화가 없기 때문입니다.

E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}b] = \int p_\theta(\tau) \nabla_\theta \log{ p_\theta(\tau)}bd \tau = \int \nabla_\theta p_\theta(\tau)bd \tau = b\nabla_\theta \int p_\theta(\tau)d \tau = b\nabla_\theta 1 = 0

b는 $\theta$ 와 관계 없는 식이고, 확률의 전 영역에서 inetgral은 1이 되기 때문에, 결국 baseline을 뺴주는 것은 expectation에 있어 unbiased가 됩니다.

사실 average of reward는 최선의 baseline은 아닙니다. 그러나 구하기 쉽기 때문에 baseline으로 더 많이 사용합니다. 그렇다면 최선의 baseline은 무엇일까요?

다음과 같은 expectation과 variance의 관계식에 의해 최선의 baseline을 구해볼 수 있습니다.

Var[x]=E[x^2]- { E[x] }^2

우리가 구하고자 하는 expectation은 다음과 같습니다.

E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}(r(\tau)-b)]

그에 해당하는 variance는 다음과 같이 전개해볼 수 있습니다.

Var = E_{\tau\sim p_\theta(\tau)}[(\nabla_\theta \log{ p_\theta(\tau)}(r(\tau)-b))^2] - E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}(r(\tau)-b)]^2

그런데 baseline은 expectation에 대해 unbiased이기 때문에 $E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}(r(\tau)-b)]^2$ 는 $E_{\tau\sim p_\theta(\tau)}[\nabla_\theta \log{ p_\theta(\tau)}r(\tau)]^2$ 로 정리할 수 있습니다. 따라서양변을 b에 대해 미분하면 다음과 같습니다.

\frac{dVar}{db} = \frac{d}{db}E[(\nabla_\theta \log{ p_\theta(\tau)}(r(\tau)-b))^2]

= \frac{d}{db}(E[(\nabla_\theta \log{ p_\theta(\tau)})^2r(\tau)^2]-2E[(\nabla_\theta \log{ p_\theta(\tau)})^2r(\tau)b]+E[(\nabla_\theta \log{ p_\theta(\tau)})^2b^2])

= -2E[(\nabla_\theta \log{ p_\theta(\tau)})^2r(\tau)]+2bE[(\nabla_\theta \log{ p_\theta(\tau)})^2] = 0

즉 variance를 최소로 만들어주는 baseline값은 다음과 같습니다.

b = \frac{E[(\nabla_\theta \log{ p_\theta(\tau)})^2r(\tau)]}{E[(\nabla_\theta \log{ p_\theta(\tau)})^2]}

해석으로는 gradient의 크기로 weighted된 return의 expectation입니다. 다만 구현의 복잡성에 있어 잘 쓰이진 않습니다.

Off-Policy Policy Gradients

on-policy vs. off-policy

지난 포스팅에서 on-policy와 off-policy의 차이점을 언급한 바 있습니다. 다시 정리해보면 다음과 같습니다.

on-policy: 그 policy로 얻은 sample만 학습에 사용할 수 있는 알고리즘입니다.
off-policy: 다른 policy로 얻은 sample도 학습에 사용할 수 있는 알고리즘입니다.

policy gradient는 on-policy입니다. 다음과 같은 목적함수 식에서 $\tau\sim p_\theta(\tau)$ 이기 때문입니다. gradient를 구하기 위해서는 그 policy를 통해 구해진 sample만 쓸 수 있다는 뜻이죠.

\nabla_\theta J(\theta) = E_{\tau\sim p_\theta(\tau)}\left[\left(\displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_t|s_t)}}\right) \left(\displaystyle\sum_{t=1}^{T}{r(s_t,a_t)} \right) \right]

기존의 데이터를 얻을 수 있어도 사용할 수 없기 때문에 on-policy은 비효율적인 방법입니다. 따라서 우리는 policy gradient를 off-policy 방법으로 사용할 수 있게 만들고 싶습니다. 그 때 이용하는 것이 importance sampling 입니다.

off-policy policy gradient with importance sampling

예를 들어 $\theta$ 으로 얻은 sample로 새로운 policy의 parameter $\theta'$ 를 학습하고 싶다고 해봅시다. 그러면 우리는 objective를 구함에 있어서 다음과 같은 expectation의 성질을 이용할 수 있습니다. 이를 importance sampling 이라고 합니다.

\begin{aligned} & \ E_{x \sim p_{\theta'}(x)}[f(x)] \\ &= \int p_{\theta'}(x) f(x) dx\\ &= \int \frac{p_\theta(x)}{p_\theta(x)}p_{\theta'}(x) f(x) dx \\ &= \int p_\theta(x) \frac{p_{\theta'}(x)}{p_\theta(x)} f(x) dx \\ &= E_{x \sim p_{\theta}(x)}\left[\frac{p_{\theta'}(x)}{p_\theta(x)}f(x)\right] \end{aligned}

따라서 objective function은 다음과 같이 정리됩니다.

\begin{aligned} J(\theta') &= E_{\tau \sim p_{\theta'}(\tau)}[r(\tau)] \\ &= E_{\tau \sim p_{\theta}(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_\theta(\tau)}r(\tau)\right] \end{aligned}

$\theta'$ 에 대한 gradient는 $\nabla_{\theta'} p_{\theta'}(\tau) = p_{\theta'}(\tau) \nabla_{\theta'} \log{p_{\theta'}(\tau)}$ 에 의해 다음과 같이 정리할 수 있습니다.

\nabla_{\theta'} J(\theta') = E_{\tau \sim p_{\theta}(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_\theta(\tau)} \nabla_{\theta'} \log{p_{\theta'}(\tau)} r(\tau)\right]

여기서 $\theta = \theta'$ 이라면 우리가 아는 policy gradient 식이 됩니다.

이 때 $p_\theta(\tau)$ 는 Markov Property에 의해 다음과 같이 정리되므로, $\frac{p_{\theta'}(\tau)}{p_\theta(\tau)}$ 를 간단히 정리해볼 수 있습니다.

p_\theta(\tau) = p(s_1) \displaystyle\prod_{t=1}^{T}\pi_\theta(a_t|s_t) p(s_{t+1}|s_t,a_t)

\frac{p_{\theta'}(\tau)}{p_\theta(\tau)} = \frac{p(s_1) \prod_{t=1}^{T}\pi_{\theta'}(a_t|s_t) p(s_{t+1}|s_t,a_t)}{p(s_1) \prod_{t=1}^{T}\pi_{\theta}(a_t|s_t) p(s_{t+1}|s_t,a_t)} = \frac{\prod_{t=1}^{T}\pi_{\theta'}(a_t|s_t) }{ \prod_{t=1}^{T}\pi_{\theta}(a_t|s_t)}

마지막 등호는 transition probability가 동일하기 때문에 약분되어 성립합니다.

이를 이용하여 gradient를 다시 써보면 다음과 같습니다.

\begin{aligned} \nabla_{\theta'} J(\theta') &= E_{\tau \sim p_{\theta}(\tau)}\left[\frac{p_{\theta'}(\tau)}{p_\theta(\tau)} \nabla_{\theta'} \log{p_{\theta'}(\tau)} r(\tau)\right] \\ &= E_{\tau \sim p_{\theta}(\tau)}\left[\left(\prod_{t=1}^{T}\frac{\pi_{\theta'}(a_t|s_t) }{ \pi_{\theta}(a_t|s_t)}\right) \left( \sum_{t=1}^{T} \nabla_{\theta'} \log{\pi_{\theta'}(a_t|s_t)} \right) \left( \sum_{t=1}^{T} r(s_t, a_t) \right) \right] \\ \end{aligned}

이 때 causality를 적용해보면 식이 다음과 같이 정리됩니다.

\nabla_{\theta'} J(\theta') = E_{\tau \sim p_{\theta}(\tau)}\left[\sum_{t=1}^{T} \nabla_{\theta'} \log{\pi_{\theta'}(a_t|s_t)} \left(\prod_{t'=1}^{t}\frac{\pi_{\theta'}(a_{t'}|s_{t'}) }{ \pi_{\theta}(a_{t'}|s_{t'})}\right) \left( \sum_{t'=t}^{T} r(s_{t'}, a_{t'}) \left(\prod_{t''=t}^{t'}\frac{\pi_{\theta'}(a_{t''}|s_{t''}) }{ \pi_{\theta}(a_{t''}|s_{t''})}\right) \right) \right] \\

첫번째 $\prod$ 항은 현재까지의 action만이 gradient에 영향을 미치기 때문이고, 두번째 $\prod$ 항은 action은 앞으로의 reward에만 영향을 미치기 때문에 등장합니다. 두번째 $\prod$ 항을 생략하면 policy iteration 알고리즘이 되며, 생략을 해도 꽤 잘 작동합니다. policy iteration에 대해서는 이후의 강의에서 더 자세히 설명합니다.

그런데 이 식에는 문제가 있습니다. $\prod_{t'=1}^{t}\frac{\pi_{\theta'}(a_{t'}|s_{t'}) }{ \pi_{\theta}(a_{t'}|s_{t'})}$ 을 살펴보면 $\frac{\pi_{\theta'}(a_{t'}|s_{t'}) }{ \pi_{\theta}(a_{t'}|s_{t'})}$ 는 $s_t$ 에 대한 $a_t$ 가 $\pi_\theta$ 로 뽑아낸 action이기 때문에 1보다 작을 확률이 매우 높습니다. 1보다 작은 수를 계속 곱하게 되니, 이 값은 $T$ 에 따라 지수적으로 감소하여 gradient vanishing 문제를 야기하게 됩니다.

그리하여 우리는 first-order approximation을 이용하여 gradient를 다르게 추정할 것입니다. 먼저 on-policy의 경우에 대한 목적함수를 다시 보면 다음과 같습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

이 경우 state와 action은 marginal probability $\pi_\theta(s_{i,t}, a_{i,t})$ 에서 sampling된 것이라 볼 수 있습니다. 따라서 우리는 이전과 같이 모든 trajectory에 대한 importance sampling을 사용하지 않고, 한 time step 각각에 대해서만 importance sampling을 사용할 수 있습니다. 그러면 식은 다음과 같이 정리됩니다. 앞선 importance sampling을 위한 유도과정을 잘 살펴보면 쉽게 이해할 수 있습니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\frac{\pi_{\theta'}(s_{t'}, a_{t'}) }{ \pi_{\theta}(s_{t'}, a_{t'})} \nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

조건부 확률의 정의에 의해 식은 다음과 같이 정리됩니다.

= \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\frac{\pi_{\theta'}(s_{t'}) }{ \pi_{\theta}(s_{t'})} \frac{\pi_{\theta'}(a_{t'}|s_{t'}) }{ \pi_{\theta}(a_{t'}|s_{t'})} \nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

이 때 $\frac{\pi_{\theta'}(s_{t'}) }{ \pi_{\theta}(s_{t'})}$ 는 거의 1이라 무시할 수 있고 따라서 이전의 식에서 gradient vanishing 없이 $t'=t$ 만 취할 수 있다는 것이 강의의 설명입니다. 생략 가능한 구체적 이유는 이후 강의에서 설명한다고 합니다.

Implementing Policy Gradients

implementation

다음과 같이 objective의 gradient를 일일이 구하여 더하는 것은 비용이 많이 듭니다.

\nabla_\theta J(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

따라서 우리는 gradient를 구하면 obejctive의 gradient가 되는 식을 먼저 구한 뒤, 그 gradient를 한 번에 구하고 싶습니다. 그 식은 다음과 같습니다.

\tilde{J}(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{ \log{\pi_\theta(a_{i,t}|s_{i,t})}} \hat{Q}_{i,t}

이는 maximum likelihood에서 따온 방법론으로, maximum likelihood에서도 다음과 같이 식을 정리합니다.

\nabla_\theta J_{ML}(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{\nabla_\theta \log{\pi_\theta(a_{i,t}|s_{i,t})}}

\tilde{J}_{ML}(\theta) \approx \frac{1}{N} \displaystyle\sum_{i=1}^{N} \displaystyle\sum_{t=1}^{T}{ \log{\pi_\theta(a_{i,t}|s_{i,t})}}

maximum likelihood 구현을 먼저 살펴보면 다음과 같습니다. discrete action에 대한 구현입니다.

먼저 policy로 prediction을 하면 각 시행에서 각 timestep에 대한 action의 확률 logits를 반환합니다(softmax 해야 우리가 원하는 $\pi_\theta(a_{i,t}|s_{i,t})$ 가 됨). 그러면 actions와 cross entropy를 계산하게 됩니다. maximum likelihood에서는 최선의 action이 정해져있으니, 선택된 action의 logits만 추출되어, 모든 시행에서 모든 t한 loss는 결국 $\tilde{J}$ 를 나타내게 됩니다. 그러면 gradient를 바로 구할 수 있죠.

이 코드를 이용해 policy gradient의 코드를 작성할 수 있습니다.

추가 된 것은 계산된 각 cross entropy에 $\hat{Q}_{i,t}$ 를 곱해주는 항 뿐입니다.

in practice

policy gradient는 high variance를 가지고 있습니다. 따라서 단순히 maximum likelihood를 이용하는 방법만으로는 충분하지 않습니다.

batch size를 크게 하는 방법을 고려할 수 있습니다.
learning rate를 조절해야합니다. policy gradient를 위한 조절 방법이 있는데, 이는 후에 배웁니다.

이로서 ch5에 대한 포스팅이 끝났습니다. advanced policy gradients 부분은 아직 이해가 부족하여, 추후에 따로 포스팅하도록 하겠습니다. 틀린 부분이나 이해가 안된 부분이 있다면 댓글 주세요!

CS285 website: https://rail.eecs.berkeley.edu/deeprlcourse/