Ch 08. 근사 알고리즘 (2)

8.3 통 채우기 문제

통 채우기 문제란?

• 통 용량 C, 물건 n개일 때 모든 물건을 가장 적은 수의 통에 채우는 문제
• 그리디 방법으로 넣을 통 결정

통 채우기 그리디 방법 4가지

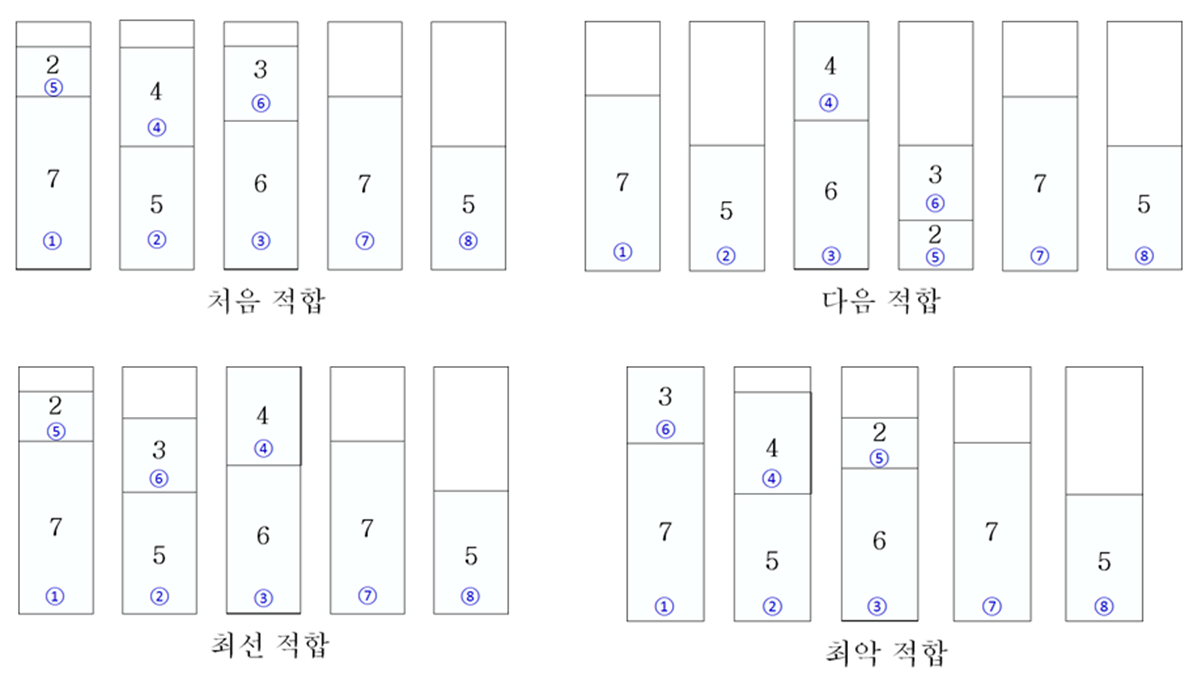
• 최초 적합 (First Fit)

  • 첫 번째 통부터 차례로 살펴보며, 가장 먼저 여유가 있는 통에 새 물건을 넣는다.

• 다음 적합 (Next Fit)

  • 직전에 물건을 넣은 통에 여유가 있으면 새 물건을 넣는다.

• 최선 적합 (Best Fit)

  • 기존의 통 중에서 새 물건이 들어가면 남는 부분이 가장 작은 통에 새 물건을 넣는다.

• 최악 적합 (Worst Fit)

  • 기존의 통 중에서 새 물건이 들어가면 남는 부분이 가장 큰 통에 새 물건을 넣는다.

• 각 방법으로 새 물건을 기존의 통에 넣을 수 없으면, 새로운 통에 새 물건을 넣는다.

과정

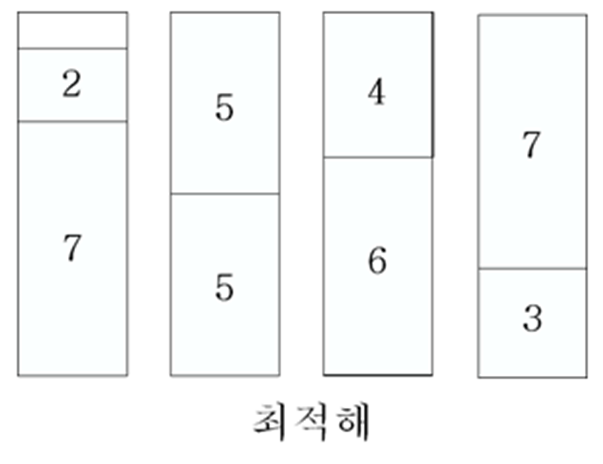
• 통의 용량 C=10, 물건의 크기가 각각 [7, 5, 6, 4, 2, 3, 7, 5]일 때
  

• 최적해
  

의사코드

• 입력: n개 물건 각각 크기
• 출력: 사용된 통의 개수

Approx_BinPacking(){
	cnt = 0   // 사용된 통의 수
	for i = 1 to n {
		if (물건 i 넣을 여유가 있는 기존의 통이 있으면)
			그리디 방법(4가지 중 1)에 따라 정해진 통에 물건 i를 넣는다.
		else
			새 통에 물건 i를 넣는다.
			cnt = cnt + 1   // 통의 수 1 증가
	}
 	return cnt
}

시간복잡도

• 최초 / 최선 / 최악 적합
  • 새 물건을 넣을 때마다 기존의 통(최대 n개)을 살펴보아야 한다.
  • $O(n^2)$
• 다음 적합
  • 직전에 사용된 통만 살펴보면 된다.
  • $O(n)$

근사 비율

• 최초 / 최선 / 최악 적합
  • 2OPT ≥ OPT’
  • 근사 비율: 2
• 다음 적합
  • 2OPT > OPT’
  • 근사 비율: 2

8.4 작업 스케줄링 문제

작업 스케줄링 문제란?

• 모든 작업이 가장 빨리 종료되도록 작업을 기계에 배정하는 문제
  • 작업: n개
  • 각 작업의 수행 시간: $t_i$, $i = 1, 2, 3, ⋯, n$
  • 기계: m개
• 그리디 알고리즘에서 배웠던 작업 스케줄링은 기계를 가장 적게 사용하도록 작업을 배정하는 문제다.(다름!)

과정

• 그리디 방법으로 작업 배정
• 현재까지 배정된 작업에 대해서 가장 빨리 끝나는 기계에 새 작업을 배정

의사코드

입력:

• 작업 n개
• 각 작업 수행 시간 $t_i, i = 1, 2, ⋯, n$
• 기계 $Mj, j = 1,2, ⋯, m$

출력: 모든 작업 종료되는 시간

Approx_JobScheduling(G){
	for j = 1 to m
	L[j] = 0           // 각 기계에 배정된 작업의 종료 시간 초기화
    
	for i = 1 to n {
		min = 1 // 종료 시간 가장 짧은 기계
		for j = 2 to m {    // 가장 일찍 끝나는 기계 찾기
			if (L[j] < L[min]) 
				min = j  
		}
	작업 i를 기계 M_min에 배정한다.
	L[min] = L[min] + t_i
	}
	return 가장 늦은 작업 종료 시간
}

시간복잡도

• n개 작업을 배정
• 마지막에 가장 큰 값 반환 시 배열 L 전체 탐색
• n x O(m) + O(m) = $O(nm)$

근사 비율

• OPT' ≤ 2xOPT
• 근사해는 최적해의 2배를 넘지 않는다

8.5 클러스터링 문제

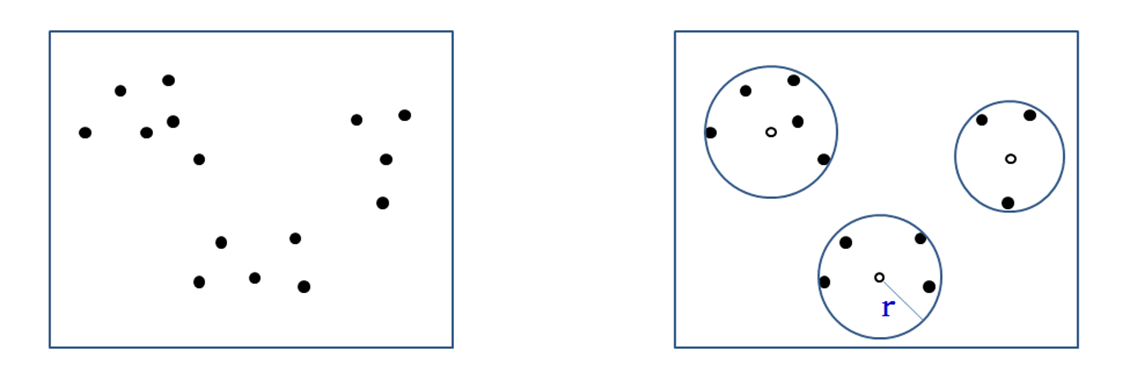
클러스터링 문제란?

• 입력으로 주어진 n개의 점을 k개의 그룹으로 나누고 각 그룹의 중심이 되는 k개의 점을 선택하는 문제
• 가장 큰 반경을 가진 그룹의 직경이 최소가 되도록 k개의 점이 선택되어야 한다.
  

과정

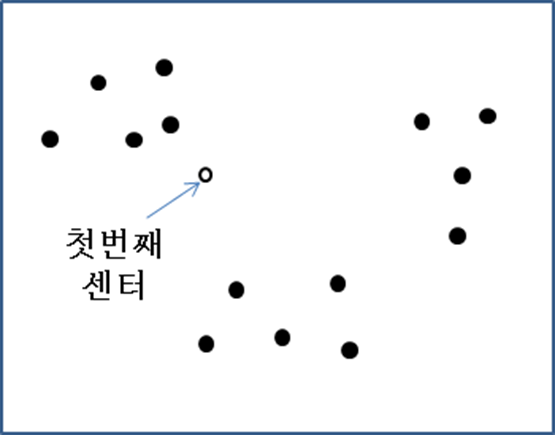
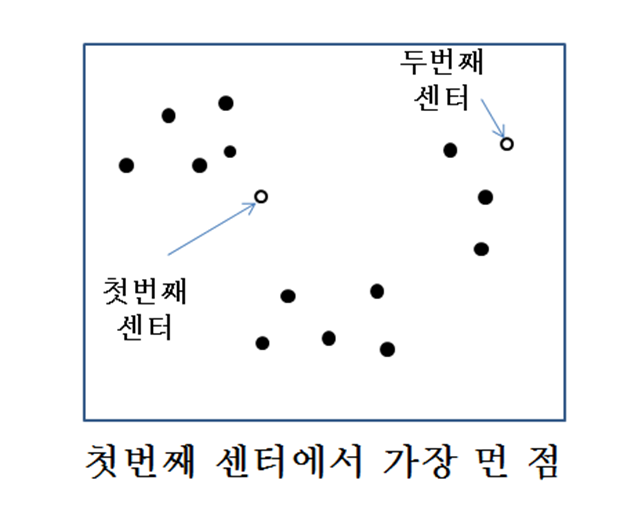
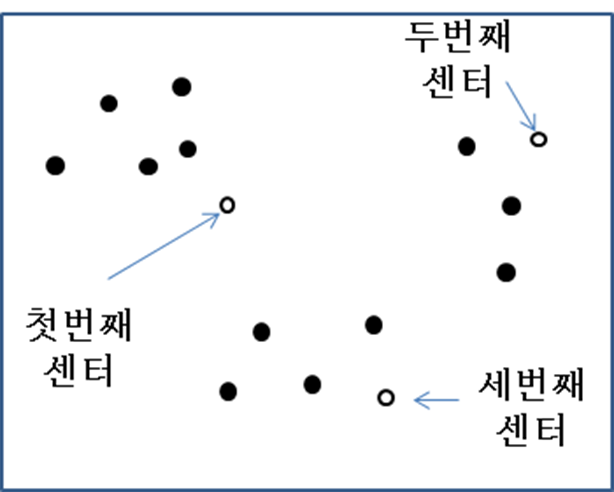
• k개의 센터 선택 방법
  • 첫번째는 랜덤하게 정해진다.
  • 정해진 센터들에서 가장 먼 점을 센터가 k개가 될 때까지 정한다.
    
    
    

의사코드

입력:

• 평면상의 점 n개($x_i, i=0,1, ... ,n-1$)
• 그룹 수 k (k>1)

출력: k개의 점의 그룹 및 각 그룹의 센터

Approx_k_Clusters(G){
	C[1] = r,  //x_r은 n개의 점 중에서 랜덤하게 선택된 점
	for j = 2 to k {
		for i = 0 to n-1 { 
			if ( x_i≠센터 ) 
			x_i와 각 센터까지의 거리를 계산
            x_i와 가장 가까운 센터까지의 거리를 D[i]에 저장
		}
	C[j] = i, //i는 배열 D의 가장 큰 원소의 인덱스이고, x_i는 센터가 아니다. 
	}
	센터가 아닌 각 점 x_i로부터 위에서 찾은 k개의 센터까지 거리를 각각 계산
    그 중 가장 짧은 거리의 센터 찾기 //이때 점 x_i는 가장 가까운 센터의 그룹에 속하게 된다.
	return 배열 C와 각 클러스터에 속한 점들의 리스트
}

시간복잡도

• O(1)+(k-1)x(O(kn)+O(n))+O(kn)
  $\therefore O(k^2n)$

근사 비율

• 2OPT ≥ 2d ≥ OPT’
• 근사 비율: 2를 넘지 않는다.