[Python] 백준 / 타일 채우기 / 2133번 / DP

DP 개념 바로가기

문제

타일 채우기 문제 링크

3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

아래 그림은 3×12 벽을 타일로 채운 예시이다.

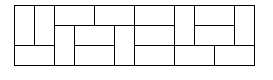
입력

첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.

2

출력

첫째 줄에 경우의 수를 출력한다.

3

접근 방식

dp 값은 타일을 채울 수 있는 경우의 수

• N이 홀수인 경우 타일을 완전히 채울 수 없다

• 3 X 2 를 채울 수 있는 경우의 수는 다음과 같다

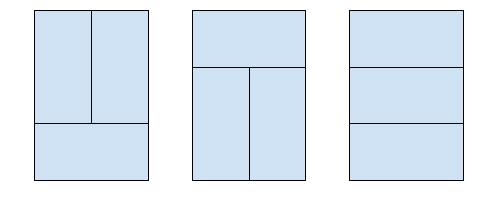
이것을 기본 형태라고 가정한다

• 3 X 4 부터는 특이한 형태가 추가되는데 다음과 같다
  
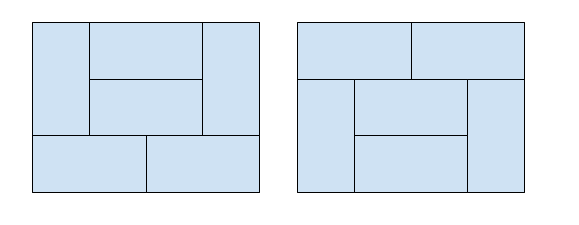
  계속 이런식으로 늘어날 수 있다
  

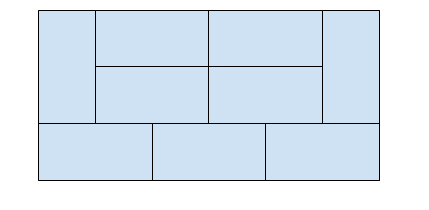
• 결국 3 X N를 채울 수 있는 경우의 수는 3가지의 경우의 수를 더한 값이다

1. N - 2 의 경우의 수에 기본 형태 3가지를 오른쪽에 붙인 경우의 수 (N - 2 경우의 수 X 3)

2. 나머지 N - 4, N - 6 .... 2 까지 모든 짝수 경우의 수에 특이한 형태를 오른쪽에 붙인 경우의 수 (N - 4, ... 2의 경우의 수 X 2)

3. 마지막엔 N의 특이한 형태 ( 2개 )

코드

# url : https://www.acmicpc.net/problem/2133
# 난이도 : silver 1

num = int(input())

dp = [0] * 31

dp[2] = 3

for n in range(4, num+1, 2):
    
    dp[n] += dp[n-2] * 3
    dp[n] += sum([dp[j] for j in range(2, n-2, 2)]) * 2
    dp[n] += 2

print(dp[num])