신경망 처음부터 끝까지 구현하기 outro
데이터 abalone.csv
- 최종 코드
# 라이브러리
import numpy as np
import pandas as pd
import csv
import matplotlib.pyplot as plt
# 랜덤 평균, 표준편차
RND_MEAN = 0
RND_STD = 0.03
# 학습률
LEARNING_RATE = 0.07
# 메인
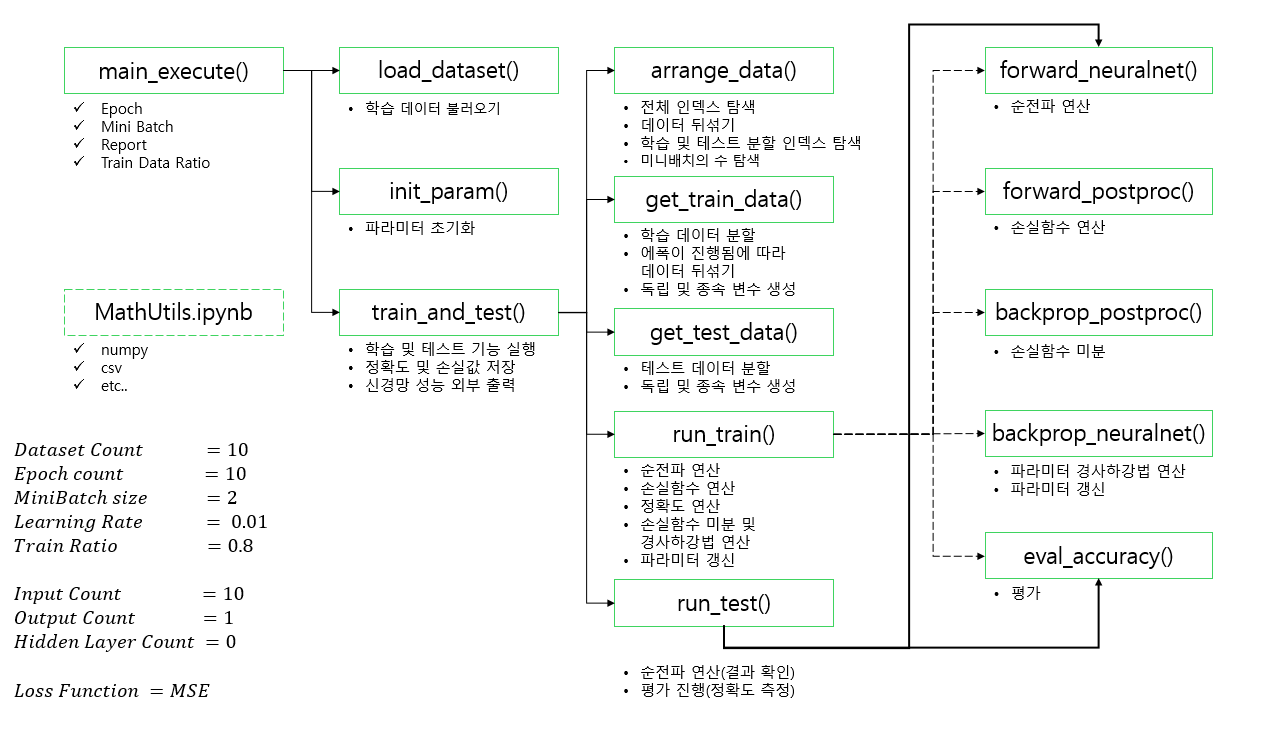
def main_execute(epoch_count = 10, mb_size = 2, report = 2, train_ratio = 0.8):
load_dataset()
weight_initial, bias_initial = init_param()
losses_mean_row, accs_mean_row, final_acc = train_and_test(epoch_count,
mb_size,
report,
train_ratio)
return weight_initial, bias_initial, losses_mean_row, accs_mean_row, final_acc
# 데이터 불러오기 -> 원핫 인코딩
def load_dataset():
with open('/content/abalone.csv') as csvfile:
csvreader = csv.reader(csvfile)
next(csvreader)
rows = []
for row in csvreader:
rows.append(row)
global data, input_cnt, output_cnt
input_cnt, output_cnt = 10, 1
data = np.zeros([len(rows), input_cnt + output_cnt])
for n, row in enumerate(rows):
if row[0] == 'M' : data[n, 0] = 1
if row[0] == 'F' : data[n, 1] = 1
if row[0] == 'I' : data[n, 2] = 1
data[n, 3 : ]= row[1:]
# 가중치, 편향 초기화
def init_param():
global weight, bias
weight_initial = []
bias_initial = []
weight = np.random.normal(RND_MEAN, RND_STD, size = [input_cnt, output_cnt])
bias = np.zeros([output_cnt])
print('==============================================')
print("Initial Weight Value : \n{}".format(weight))
print()
print("Initial Bias Value : \n{}".format(bias))
print('==============================================')
weight_initial.append(weight)
bias_initial.append(bias)
return weight_initial, bias_initial
# 훈련 데이터와 테스트 데이터로 나누고 훈련 데이터를 mini_batch 크기로 나눈 값 저장
def arrange_data(mb_size, train_ratio):
global shuffle_map, test_begin_index
shuffle_map = np.arange(data.shape[0])
np.random.shuffle(shuffle_map)
mini_batch_step_count = int(data.shape[0] * train_ratio) // mb_size
test_begin_index = mini_batch_step_count * mb_size
return mini_batch_step_count
# 테스트 데이터를 X_test와 y_test로 나눔
def get_test_data():
test_data = data[shuffle_map[test_begin_index:]]
return test_data[ : , : -output_cnt], test_data[ : , -output_cnt : ]
# 훈련 데이터를 X_train과 y_train으로 나눔
def get_train_data(mb_size, n):
if n == 0:
np.random.shuffle(shuffle_map[:test_begin_index])
train_data = data[shuffle_map[mb_size * n : mb_size * (n+1) ]]
return train_data[ : , : -output_cnt], train_data[ : , -output_cnt : ]
# 데이터 학습 도중 정확도와 손실 및 테스트 정확도 저장
def train_and_test(epoch_count, mb_size, report, train_ratio):
mini_batch_step_count = arrange_data(mb_size, train_ratio)
test_x, test_y = get_test_data()
losses_mean_row = []
accs_mean_row = []
for epoch in range(epoch_count):
losses = []
accs = []
for n in range(mini_batch_step_count):
train_x, train_y = get_train_data(mb_size, n)
loss, acc = run_train(train_x, train_y)
losses.append(loss)
accs.append(acc)
if report > 0 and (epoch + 1) % report == 0:
acc = run_test(test_x, test_y)
print("Epoch {} : Train - Loss = {:.3f}, Accuracy = {:.3f} / Test - Accuracy = {:.3f}".\
format(epoch + 1, np.mean(losses), np.mean(accs), acc))
losses_mean = np.mean(losses)
accs_mean = np.mean(accs) * 100
losses_mean_row.append(losses_mean)
accs_mean_row.append(accs_mean)
final_acc = run_test(test_x, test_y)
print("=" * 30, "Final TEST", "=" * 30)
print("\nFinal Accuracy : {:.3f}".format(final_acc))
return losses_mean_row, accs_mean_row, final_acc
# 순전파 계산 ( x 행렬과 가중치 행렬곱에 편향을 더해 y_hat에 저장 => 예측 값)
def forward_neuralnet(x):
y_hat = np.matmul(x, weight) + bias
return y_hat, x
# Mean Square Error
def forward_postproc(y_hat, y):
diff = y_hat - y
square = np.square(diff)
loss = np.mean(square)
return loss, diff
# 평가
def eval_accuracy(y_hat, y):
mdiff = np.mean(np.abs((y_hat - y) / y))
return 1 - mdiff
# 손실함수 미분
def backprop_postproc(diff):
M_N = diff.shape
g_mse_square = np.ones(M_N) / np.prod(M_N)
g_square_diff = 2 * diff
g_diff_output = 1
G_diff = g_mse_square * g_square_diff
G_output = g_diff_output * G_diff
return G_output
# 경사하강법 및 파라미터 갱신
def backprop_neuralnet(G_output, x):
global weight, bias
x_transpose = x.transpose()
G_w = np.matmul(x_transpose, G_output)
G_b = np.sum(G_output, axis = 0)
weight -= LEARNING_RATE * G_w
bias -= LEARNING_RATE * G_b
# 순전파, MSE연산 후 손실함수 미분, 경사하강법으로 파라미터 갱신
def run_train(x, y):
y_hat, aux_nn_x = forward_neuralnet(x)
loss, aux_pp_diff = forward_postproc(y_hat, y)
accuracy = eval_accuracy(y_hat, y)
G_output = backprop_postproc(aux_pp_diff)
backprop_neuralnet(G_output, aux_nn_x)
return loss, accuracy
# 순전파 연산 후 정확도 계산
def run_test(x,y):
y_hat, _ = forward_neuralnet(x)
accuracy = eval_accuracy(y_hat, y)
return accuracy
weight_initial, bias_initial, losses_mean_row, accs_mean_row, final_acc = main_execute(epoch_count = 100,
mb_size = 32,
report = 10,
train_ratio = 0.8)
print('==============================================')
print("changed weight \n", weight)
print()
print("changed bias \n", bias)
print('==============================================')
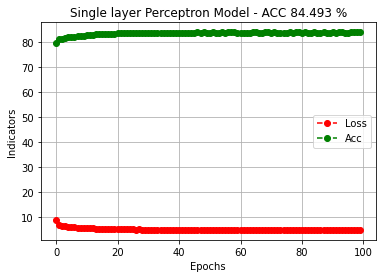
plt.plot(losses_mean_row, '--o', color = 'red', label = 'Loss')
plt.plot(accs_mean_row, '--o', color = 'green', label = 'Acc')
plt.title("Single layer Perceptron Model - ACC {:.3f} %".\
format(final_acc * 100))
plt.xlabel("Epochs")
plt.ylabel("Indicators")
plt.grid()
plt.legend()
plt.show()- 실행 결과
==============================================
Initial Weight Value :
[[ 0.00392687]
[-0.03023993]
[-0.01874033]
[-0.01190798]
[ 0.00395032]
[-0.03944189]
[-0.00296807]
[-0.00039526]
[-0.04362359]
[-0.04090817]]
Initial Bias Value :
[0.]
==============================================
Epoch 10 : Train - Loss = 5.787, Accuracy = 0.825 / Test - Accuracy = 0.834
Epoch 20 : Train - Loss = 5.303, Accuracy = 0.833 / Test - Accuracy = 0.840
Epoch 30 : Train - Loss = 5.158, Accuracy = 0.835 / Test - Accuracy = 0.846
Epoch 40 : Train - Loss = 5.093, Accuracy = 0.837 / Test - Accuracy = 0.845
Epoch 50 : Train - Loss = 5.059, Accuracy = 0.836 / Test - Accuracy = 0.848
Epoch 60 : Train - Loss = 5.060, Accuracy = 0.836 / Test - Accuracy = 0.847
Epoch 70 : Train - Loss = 5.035, Accuracy = 0.837 / Test - Accuracy = 0.841
Epoch 80 : Train - Loss = 5.045, Accuracy = 0.837 / Test - Accuracy = 0.843
Epoch 90 : Train - Loss = 5.032, Accuracy = 0.837 / Test - Accuracy = 0.844
Epoch 100 : Train - Loss = 5.031, Accuracy = 0.837 / Test - Accuracy = 0.845
============================== Final TEST ==============================
Final Accuracy : 0.845
==============================================
changed weight
[[ 1.31452981]
[ 1.31307042]
[ 0.25433609]
[ 3.48375914]
[ 6.19192754]
[ 6.50558166]
[ 5.92247413]
[-17.15839346]
[ -4.83310333]
[ 12.32289052]]
changed bias
[2.92698972]
==============================================