지도학습 - 선형회귀 (Linear Regression) 개념
회귀 모델
-
어떤 자료에 대하여 그 값에 영향을 주는 조건을 고려하여 구한 평균
(어떤 데이터들은 굉장히 크거나 작을지라도 전체적으로 이 데이터들은 전체 평균으로 회귀하려는 특징이 있다는 통계학 기법) -
y = h(x1, x2, x3 ..xk; w1, w2, w3 ... wk) + e
h() : 조건에 따른 평균을 구하는 함수 (회귀 모델)
x : 어떤 조건(특성)
w : 각 조건의 영향력(가중치)
e : 오차항 / 다양한 현실적인 한계로 발생하는 불확실성 / 일종의 잡음(noise)
선형 모델
- 입력 특성에 대한 선형 함수를 만들어 예측을 수행
- 다양한 선형 모델이 존재
- 분류와 회귀에 모두 사용 가능
비용 함수
- 그려진 직선(H(x))와 실제 데이터(y)의 차이
- Cost의 총 합이 작은 H(x)일수록 데이터를 잘 대변하는 훌륭한 Linear Regression
- Cost는 양수일 수도 음수일 수도 있기 때문에 Cost의 총 합을 구할 때 각 Cost값을 제곱하여 평균을 내는 방식(MSE)을 사용
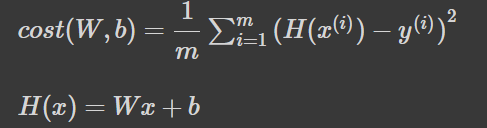
머신러닝에서 learning의 목적은 Cost를 정의하고 이를 최소화하는 것
Cost를 최소로 하는 방법 (경사하강법)
- 경사 하강법 = Gradient descent algorithm
- 점진적인 하강, 점진적으로 반복적인 계산을 통해 가중치 값을 업데이트 하면서 오류 값이 최소가 되는 값을 구하는 방식
- 함수의 기울기를 구하여 기울기가 낮은 쪽으로 계속 이동하여 값을 최적화 시키는 방법(오차가 가장 작은 방향으로 이동시키는 방법)
