고정 소수점 & 부동 소수점

고정 소수점

• 움직이지 않고 고정된 소수점이라는 의미 즉, 소수점 아래 숫자가 있는 실수들을 표기하는 방식을 고정 소수점으로 하는 것

• 이것은 10진수를 2진수로 바꿨다고 했을 때 그 값을 그대로 활용함을 의미함

• 컴퓨터는 2진수로 수를 취급하기 때문에 고정 소수점, 부동 소수점을 활용하는 것

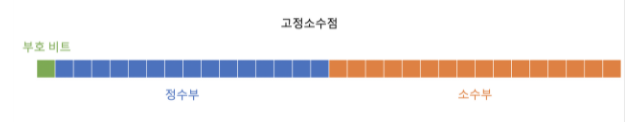
• 32비트 상황에서 고정 소수점을 나타내면 아래와 같음

• 부호 비트는 실수의 부호를 나타내는 것으로 음수면 1, 양수면 0임

• 정수부는 실수의 정수 부분을 두는 것임

• 소수부는 실수의 소수 부분을 둠

• 21.25를 2진수 10101.01 바꿀 때 부호비트는 0 정수부는 10101 소수부는 01이 되어 아래와 같이 표기 가능

• 여기서 나머지 빈 부분은 다 0으로 채움

부동 소수점

• 부동 소수점도 똑같이 부호 비트를 나타내고 그 다음 8칸은 지수부, 나머지 23칸은 가수부임(32비트 기준)

• 지수부의 경우 n에 bias를 더한 값을 2진수로 변환한 수를 넣는 부분임(bias는 32비트에서 127, 64비트에서 1023임)

• 여기서 부동소수점 표현시 R=(+-)m x 2^n인데 m은 1.xxxx의 형태로 만드는 것으로 정해져 있음(IEEE 표준에 따라서)

• 이를 표기법에 맞게 처리하면 21.25를 예를 들어본다면 2진수르 10101.01임

• 여기서 각각 R, m, n을 구할 수 있는데 R의 경우 10101.01이고 m은 1.010101, n은 4가 됨 즉, R = 1.010101 x 2^4로 표기 가능

• 여기서 부동 소수점 표현을 활용하여서 지수부의 경우 n에 bias를 더한 값인데 여기서 n은 4이고 여기다가 bias의 경우 32비트이므로 127임 그래서 지수부는 n + bias = 4 + 127 = 131이 됨

• 이를 2진수 변환을 해 지수부는 10000011임

• 가수부의 경우 m의 소수점 아래 부분을 말함, m은 1.010101임, 그래서 010101이 가수부가 됨

• 이를 부동 소수점을 채우면 아래와 같음

• 그리고 여기도 똑같이 0으로 모두 채워넣을 수 있음

• 이 부동 소수점을 사용하는 이유는 고정 소수점의 경우 일정 자릿수보다 큰 수를 다룰 수 없는 경우가 생김

• 하지만 이때 부동 소수점을 사용한다면 정수, 소수 대신 가수, 지수를 다루기 때문에 자릿수보다 큰 상황에서도 사용이 가능함 즉, 제약이 어느정도 없어짐 그래서 이 점이 직접적으로 쓰는데 있어서 크게 작용함