패리티 비트
-
정보의 전달 과정에서 오류가 생겼는지를 검사하기 위해 추가된 비트임
-
문자열 내 1비트의 모든 숫자가 짝수 또는 홀수인지를 보증하기 위해 전송하고자 하는 데이터의 각 문자에 1비트를 더하여 전송하는 방법임
-
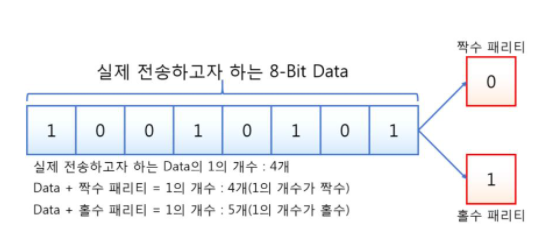
짝수 패리티는 전체 비트에서 1의 개수가 짝수가 되도록 패리티 비트를 정하는 것임
-
홀수 패리티는 전체 비트에서 1의 개수가 홀수가 되도록 패리티 비트를 정하는 것임
-
이 예시를 보면 아래와 같음
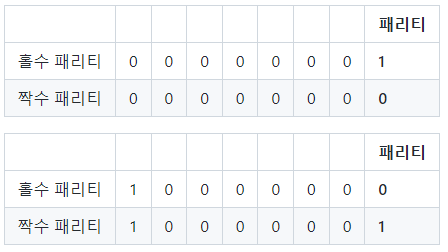
- 이런식으로 패리티 비트를 활용해서 오류 발생 여부를 알 수 있긴 함, 단 수정이 불가능하고 아래와 같이 오류의 개수에 따라서 오류를 검출하지 못하는 경우가 발생할 수도 있음
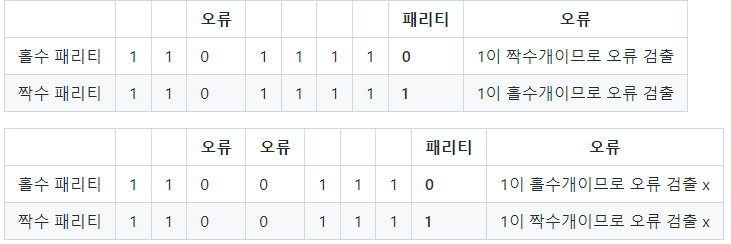
병렬 패리티 블록합 검사
- 여기서 위와 같은 문제가 발생할 수 있기 때문에 이를 보완하기 위해서 에러를 검출하기 위한 세로 중복 검사가 있음, 아래와 같이 볼 수 있는데
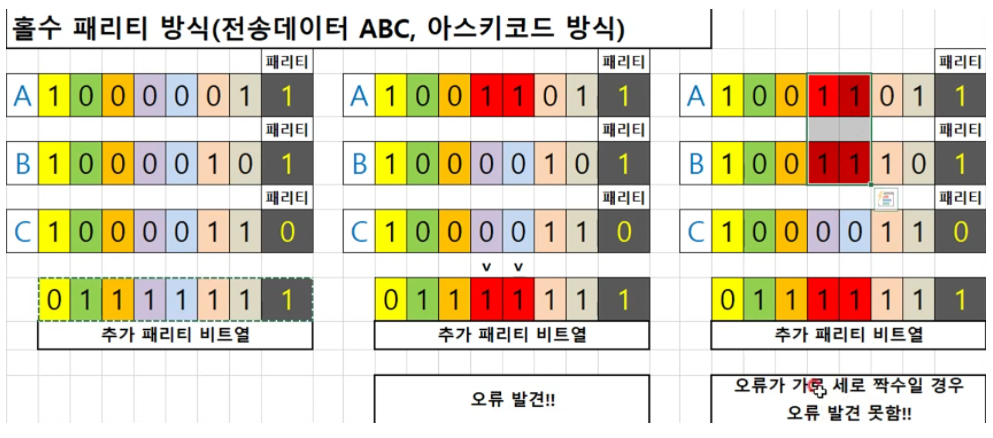
-
위의 방식대로면 홀수 패리티이기 때문에 A,B,C의 각각 가로가 홀수 패리티를 만족하고 추가 패리티 비트열 역시 세로로 홀수 패리티를 만족해야하는 방식임
-
그래서 오류 발견한 경우 세로의 방향에서 홀수 패리티를 만족을 못하기 때문에 오류가 발견된 것, 하지만 여기서도 역시 오류가 발견되지 못하는 경우가 있음(짝수 패리티의 경우도 동일함)
-
여전히 오류를 발견할 수 없는 경우에서는 해밍 코드방식이 필요함
해밍 코드
-
해밍 코드는 오류 검출과 정정을 할 수 있는 코드임
-
데이터ㅓ 비트를 보고 1비트에 대한 오류를 정정할 곳을 찾아 수정할 수 있고, 많은 양의 데이터 전송시 유리함, 2비트의 오류도 검출 가능함
-
패리티 비트의 개수는 아래와 같이 판단할 수 있음

-
위처럼 2^n번째 비트가 오류 검출을 위한 패리티 비트임
-
여기서 패리티 규칙(짝수 or 홀수)이 정해졌다면 n번째 패리티 비트는 n번째 비트에서 시작하여 n비트만큼 포함하고, n비트씩 건너뛴 비트들을 대상으로 패리티 비트를 결정할 수 있음, 이를 보면 아래와 같음
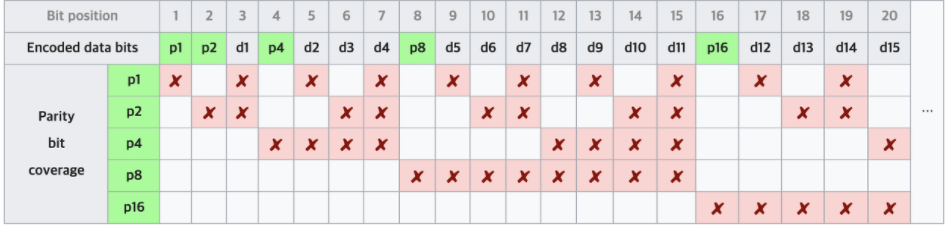
-
여기서 예시로 14를 홀수 패리티 방식으로 해밍코드를 적용하면, 먼저 이진수로는
1110이고, 위의 공식을 생각해보면2^3 >= 4 + 3으로 패리티 비트 개수는 3으로 결정됨 -
그리고 패리티 비트는
2^n번째 비트에 들어감(1,2,4,8,...) -
이를 그대로 본다면 아래와 같음
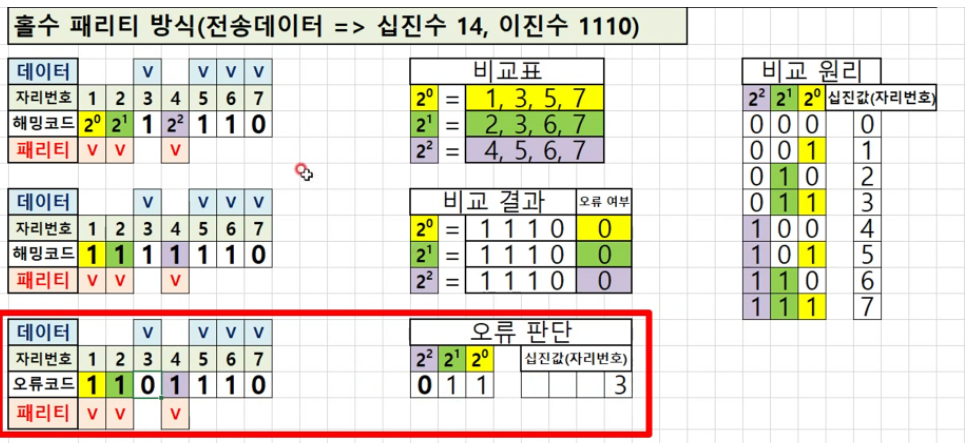
-
패리티 비트는 1,2,4에 들어가게 되고, 패리티 규칙상 패리티 비트는 n비트씩 건너뛴 비트를 상태로 결정한다고 했음
-
그래서
2^0인 경우가 1비트만큼 포함하고 1비트씩 건너뛴 비트를 대상으로 해서 비교표에서 보듯이1,3,5,7을 비교하는 것임 그러면 해밍코드가 들어가는 것을 제외하고3,5,7을 보면110임 여기서 홀수 패리티 방식이므로2^0은1이 들어가 비교 결과에1110이 들어가는 것임 -
마찬가지로
2^1의 경우도 비교표에서 보듯이 2비트만큼 포함하고 2비트씩 건너뛴 비트임 그래서2,3,6,7이 됨, 여기서2^1해밍코드가 들어간 곳을 빼면110임 그래서 홀수 패리티이므로 패리티 비트까지 넣으면1110이 되야해서1이 들어감,2^2의 경우도 동일하게 적용됨 -
그래서 오류 검출전까진 문제가 없고 비교 결과 오류 여부가 없는 것임
-
근데 여기서 오류가 난 경우에 대해서 판단을 해보면 3번째 자리코드가 0으로 바뀐 것임
-
그런데 여기서 위에서 해밍코드 방식으로 비교를 해보면
2^0의 경우1010,2^1도1010,2^2은1110이 됨, 그러면 홀수 패리티인데2^0,2^1모두 오류 검출로 오류 여부가1로 됨 -
그래서 오류판단에서
2^0,2^1은1이고2^2이0이라서 이를 그대로 진수변환하면3이됨, 즉,3에 오류가 생긴 것을 알 수 있음, 이런식으로 오류 검출과 수정이 가능함