NumPy ndarray 개요
NumPy 학교 강의도 듣고, 유튜브도 봤는데, 그래서 어떻게 쓰이는지를 모르겠다.
단순 개념보다는 머신러닝에서 어떻게 활용 되는지에 중점을 두고 알아보자
ndarray: N 차원 (Dimension) 배열 (Array) 객체
파이썬 기본 list도 있는데 이걸 안 쓰고 왜 굳이 ndarray?
- 파이썬 list로는 대용량 데이터를 처리하기 힘듦, ndarray는 훨씬 빠르게 처리
- scikit-learn도 ndarray 기반으로 작성되어 있음, 반환도 ndarray로 함
list를 ndarray로 변환하는 코드 예시
array1 = np.array([1,2,3])
array2 = np.array([[1,2,3], [4,5,6]])ndarray shape (중요)
shape, 차원 예시
1. array: [1 2 3]
1차원, shape: (3, ) -> 이렇게 생긴 건 무조건 1차원 그냥 암기 할 것
2. array: [[1 2 3][4 5 6]]
2차원, shape: (2, 3)
3. array: [[1 2 3]]
2차원, shape: (1, 3) -> 2차원인 것 확인
ndarray type
- ndarray는 데이터 값으로 숫자, 문자열, bool 등 모두 가능
- 한 ndarray에는 모두 동일한 데이터 타입만 가능
- 대용량 데이터를 다룰 시 64bit float형 보다는 8bit/16bit의 integer형이 훨씬 메모리를 절약
type 변경 예시 코드
array = [1.0, 2.0]
array_int = array.astype("int32")ndarray axis
ndarray는 행, 열, 높이의 개념이 없음
axis0, axis1, axis2, ... 이렇게 axis 단위로 차원이 부여됨
1차원 배열 - axis0
2차원 배열 - axis0: 행의 방향, axis1: 열의 방향
3차원 배열 - axis0: depth(높이, 깊이)의 방향, axis1: 행의 방향, axis2: 열의 방향
"맨 뒤에 있는 axis가 가장 깊숙히 들어있는 원소의 방향 (그림 참고)"
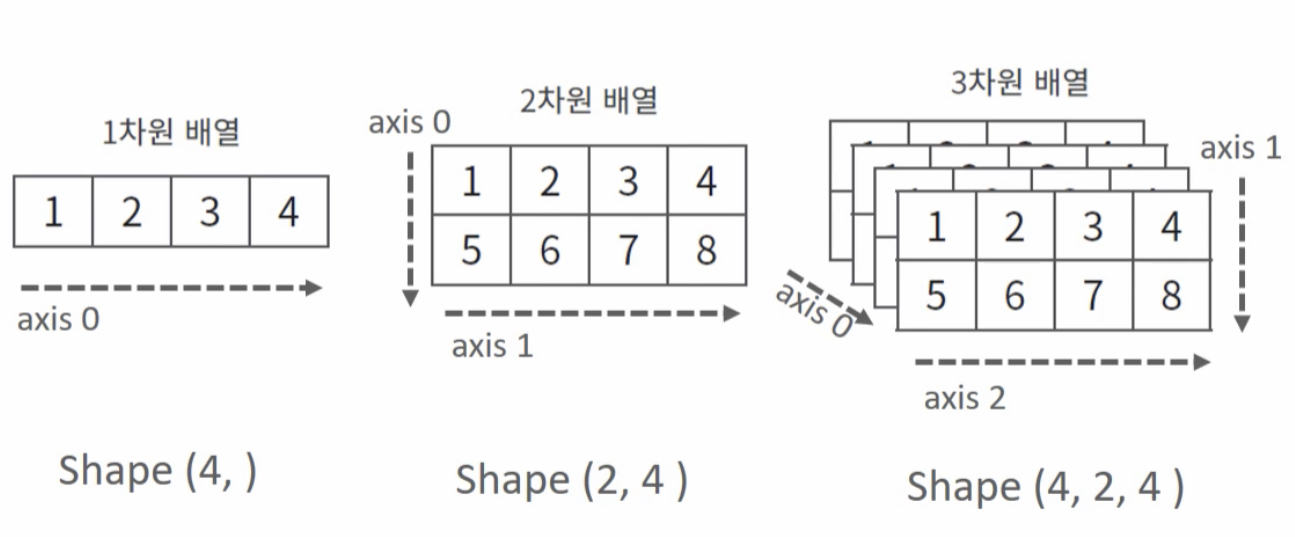
머신러닝을 할 때는 거의 2차원까지라 그냥 0이 행방향, 1이 열방향으로 외워도 됨!
다만 딥러닝에서는 다차원을 사용함
ndarray reshape (중요)
reshape: ndarray의 차원을 변경하는 함수
만약-1이 들어가면 가변적으로나머지 axis에 맞춰줌 -> 아래 예시 확인
array1 = np.array([1, 2, 3, 4, 5, 6])
array2 = array1.reshape((2, 3))
array3 = array1.reshape((3, 2))
array4 = array1.reshape((-1, 3))
array5 = array1.reshape(-1, )<출력 결과>
array1
[1 2 3 4 5 6]
array2
[[1 2 3]
[4 5 6]]
array3
[[1 2]
[3 4]
[5 6]]
array4
[[1 2 3]
[4 5 6]]
array5
[1 2 3 4 5 6]
arange, zeros, ones
특정 ndarray를 만드는 함수들
예시로 이해하기
sequence_array = np.arange(10)
zero_array = np.zeros((3,2),dtype='int32')
one_array = np.ones((3,2))<출력 결과>
sequence_array
[0 1 2 3 4 5 6 7 8 9]
zero_array
[[0 0]
[0 0]
[0 0]]
one_array
[[1. 1.]
[1. 1.]
[1. 1.]]
그래서 이걸 언제 쓰는데?
"어떤 데이터가 들어가는지는 모르지만 만들어질 데이터의 차원(크기)는 알고 있을 때 초기화 용도로 사용!"
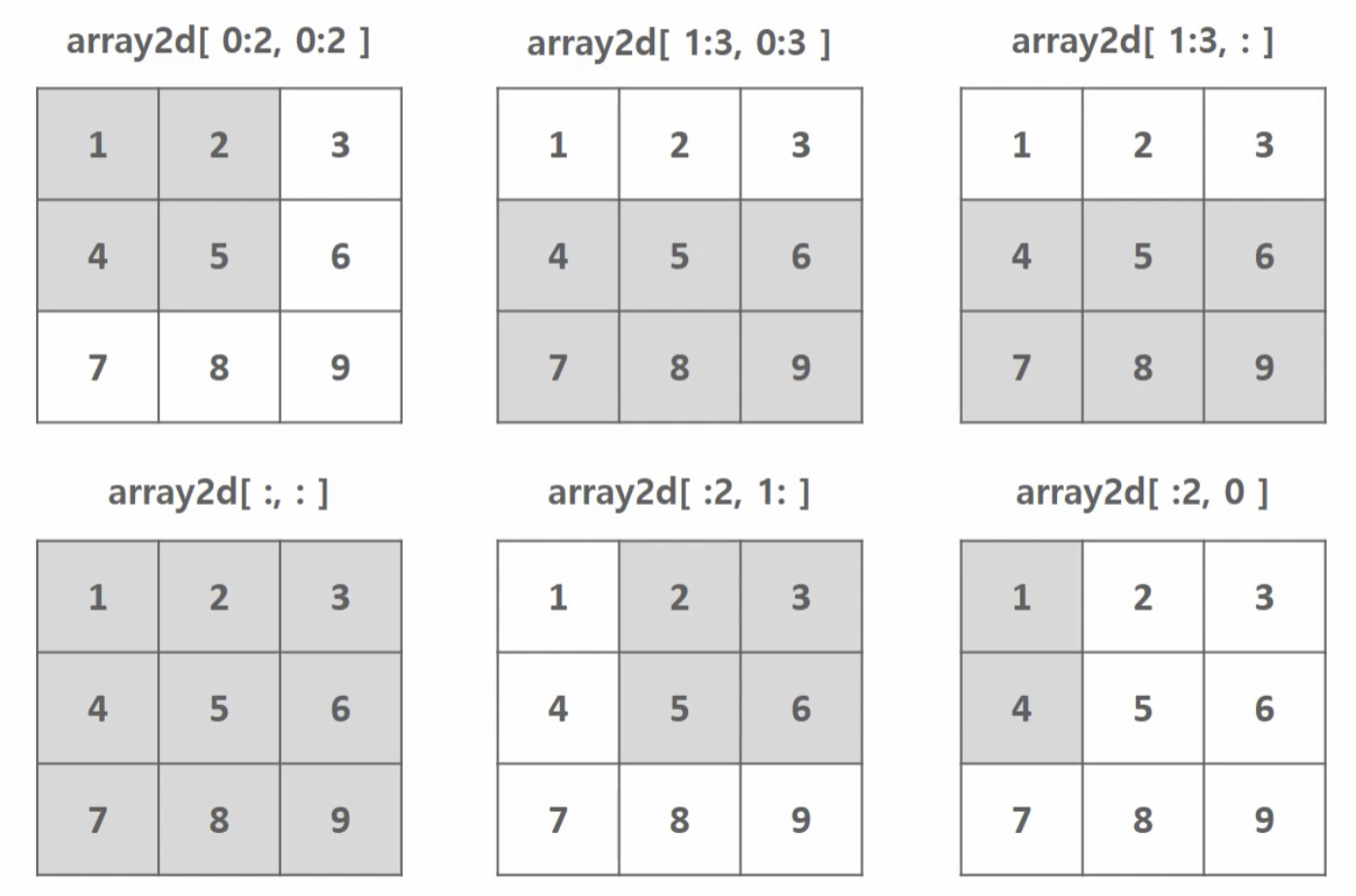
인덱싱 (indexing)
- 단일 값 추출
- 슬라이싱 (Slciing): [1:], [3:], [:] 이런 것임
- 팬시 인덱싱(Fancy indexing)
- 불린 인덱싱 (Boolean indexing) [중요]
이해하기 어렵지 않으니 예시 코드와 그림 확인
1. 단일 값 추출
1. 1차원
array = np.arange(start=1, stop=10) value = array1[2]array: [1 2 3 4 5 6 7 8 9]
value: 3
2. 2차원array1d = np.arange(start=1, stop=10) array2d = array1d.reshape(3,3)array2d
[[1 2 3]
[4 5 6]
[7 8 9]]
array2d[0,0]: 1
array2d[0,1]: 2
array2d[1,0]: 4
array2d[2,2]: 9
2. 슬라이싱 (Slicing)
사진 참조
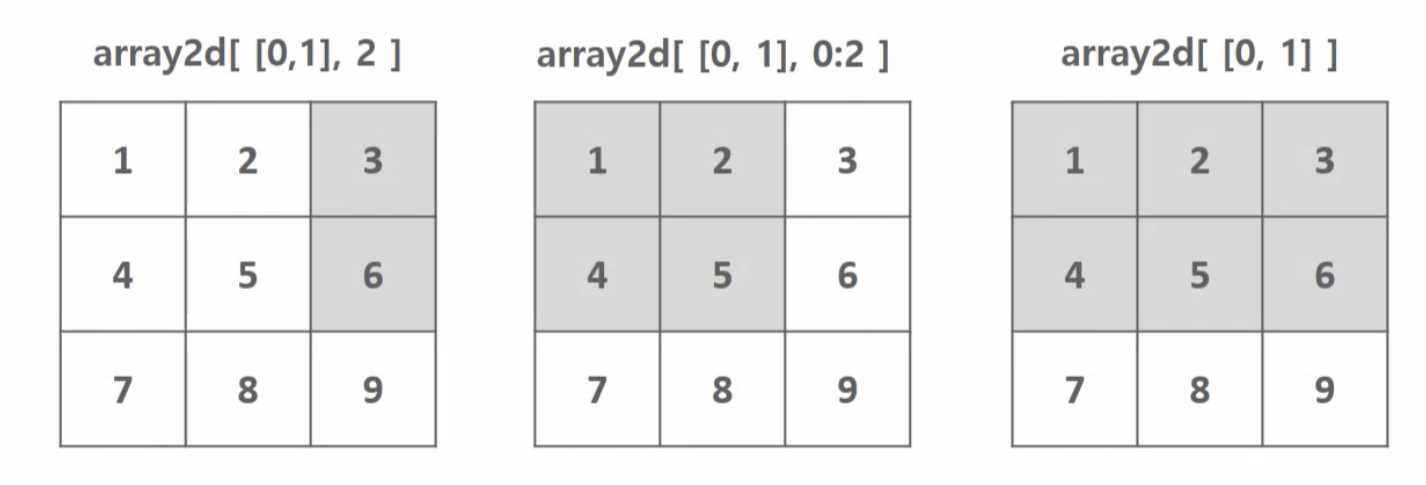
3. 팬시 인덱싱 (Fancy Indexing)
list나ndarray로 인덱스 집합을 지정하는 것
array1d = np.arange(start=1, stop=10)
array2d = array1d.reshape(3,3)
array3 = array2d[[0,1], 2]
array4 = array2d[[0,1], 0:2]
array5 = array2d[[0,1]]
print(array3, '\n')
print(array4, '\n')
print(array5)[3 6]
[[1 2]
[4 5]]
[[1 2 3]
[4 5 6]]4. 불린 인덱싱 (Boolean indexing)
조건 필터링과 검색을 동시에 할 수 있음
아래 예시 코드를 하나하나 보면 이해 가능
array1d = np.arange(start=1, stop=10)
condition = (array1d > 5)
array_condition = array1d[array1d > 5]
print(array1d)
print(condition)
print(array_condition)[1 2 3 4 5 6 7 8 9]
[False False False False False True True True True]
[6 7 8 9]sort(), argsort()
sort()는 값에 대해서 정렬한 것의 값을 구함
argsort()는 값에 대해서 정렬한 것의 인덱스를 구함
1. sort()
- np.sort(): 원 행렬을 그대로 유지한 채 원 행렬의 정렬된 행렬을 반환
- ndarray.sort(): 원행렬 자체를 정렬한 형태로 변환 (반환 값은 None) (inplace = True 느낌?)
org_array = np.array([ 3, 1, 9, 5])
print('원본 행렬:', org_array)
# np.sort( )로 정렬
sort_array1 = np.sort(org_array)
print ('np.sort( ) 호출 후 반환된 정렬 행렬:', sort_array1)
print('np.sort( ) 호출 후 원본 행렬:', org_array)
# ndarray.sort( )로 정렬
sort_array2 = org_array.sort() # 이렇게 쓰지 말 것!
print('org_array.sort( ) 호출 후 반환된 행렬:', sort_array2)
print('org_array.sort( ) 호출 후 원본 행렬:', org_array)
sort_array1_desc = np.sort(org_array)[::-1] # 내림차순
print ('내림차순으로 정렬:', sort_array1_desc) 원본 행렬: [3 1 9 5]
np.sort( ) 호출 후 반환된 정렬 행렬: [1 3 5 9]
np.sort( ) 호출 후 원본 행렬: [3 1 9 5]
org_array.sort( ) 호출 후 반환된 행렬: None
org_array.sort( ) 호출 후 원본 행렬: [1 3 5 9]
내림차순으로 정렬: [9 5 3 1]<br>axis 활용한 정렬
array2d = np.array([[8, 12],
[7, 1 ]])
sort_array2d_axis0 = np.sort(array2d, axis=0)
print('행방향 정렬:\n', sort_array2d_axis0)
sort_array2d_axis1 = np.sort(array2d, axis=1)
print('열방향 정렬:\n', sort_array2d_axis1)행방향 정렬:
[[ 7 1]
[ 8 12]]
열방향 정렬:
[[ 8 12]
[ 1 7]]2. argsort()
org_array = np.array([ 3, 1, 9, 5])
sort_indices = np.argsort(org_array)
print('행렬 정렬 시 원본 행렬의 인덱스:', sort_indices)
sort_indices_desc = np.argsort(org_array)[::-1]
print('행렬 내림차순 정렬 시 원본 행렬의 인덱스:', sort_indices_desc)행렬 정렬 시 원본 행렬의 인덱스: [1 0 3 2]
행렬 내림차순 정렬 시 원본 행렬의 인덱스: [2 3 0 1]dot(), transpose()
dot()행렬 곱 함수
A = np.array([[1, 2, 3],
[4, 5, 6]])
B = np.array([[7, 8],
[9, 10],
[11, 12]])
dot_product = np.dot(A, B)
print(dot_product) [[ 58 64]
[139 154]]
transpose()전치행렬 함수
A = np.array([[1, 2],
[3, 4]])
transpose_mat = np.transpose(A)
print(transpose_mat)[[1 3]
[2 4]]NumPy 최종 정리
- NumPy는 파이썬 머신러닝을 구성하는 핵심 기반으로 반드시 이해 필요!
- NumPy API 범위는 매우 넓음, 다 하려면 지치니까 머신러닝에 필요한 것 우선
- Pandas에 비해 불친절함, 2차원 데이터 가공은 Pandas가 더 효율적