DBSCAN 개요
DBSCAN, Density Based Spatial Clustering of Applications with Noise
특정 공간 내에 데이터 밀도 차이 기반 알고리즘으로 하고 있어서 복잡한 기하학적 분포도를 가진 데이터 세트에 대해서도 군집화를 잘 수행
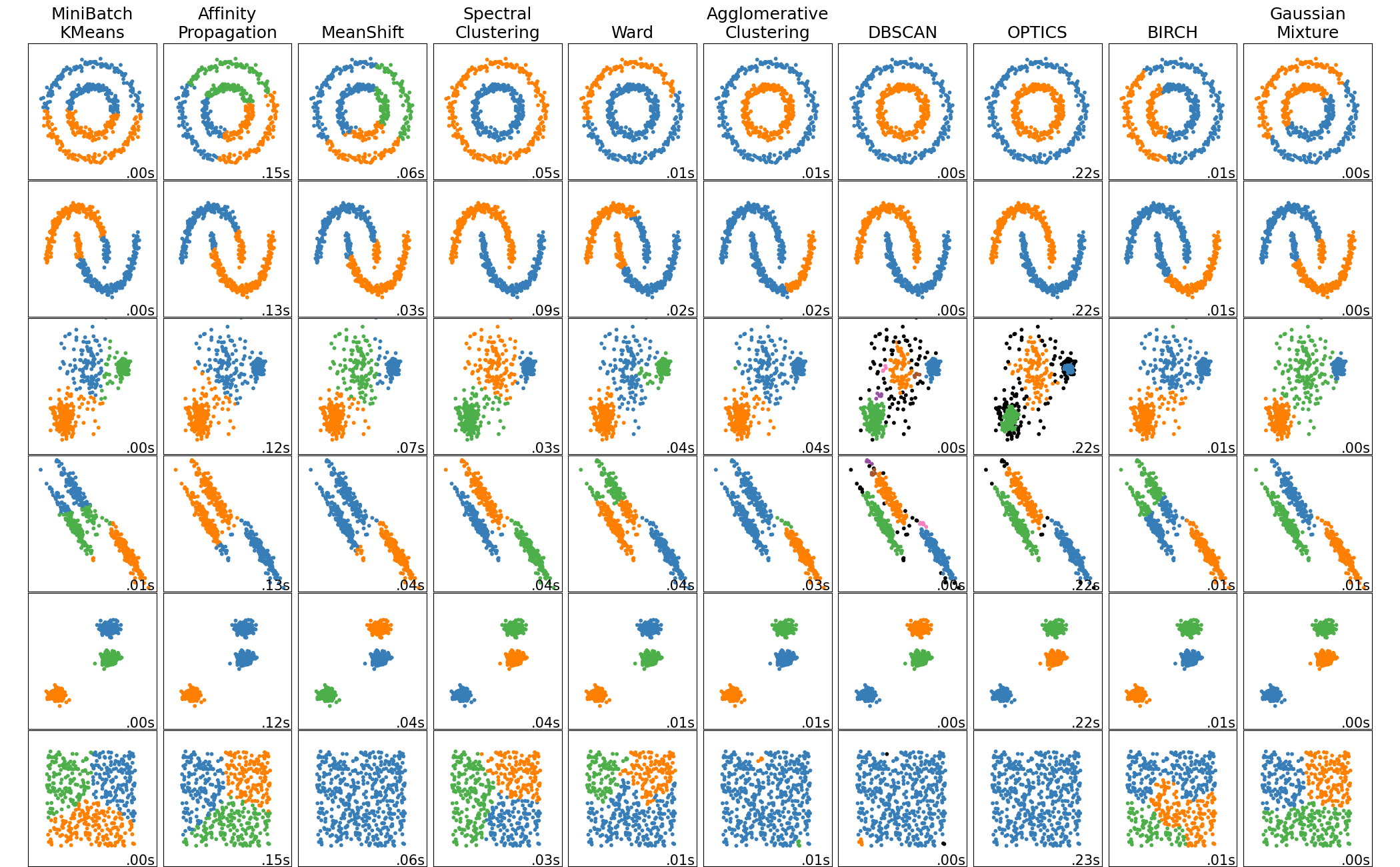
여러 데이터에 형태에 대해 각 군집화 방법을 비교해보자
https://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_comparison.html#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py
DBSCAN은 첫 번째 데이터 같은 요상한 모양도 잘 구분함!
단, 밀도 기반이라 세 번째 데이터 같이 밀도가 자주 변하는 데이터에 대해서는 아예 군집화에 실패하는 데이터들이 생길 수 있음!
DBSCAN 특징
- 알고리즘이 데이터 밀도 차이를 자동으로 감지하며 군집을 생성하므로 사용자가 군집 개수를 지정할 수 없음
- DBSCAN은 데이터 밀도가 자주 변하거나, 아예 모든 데이터의 밀도가 크게 변하지 않으면 군집화 성능이 떨어짐
- Feature의 개수가 많으면 군집화 성능이 떨어짐
구성하는 가장 중요한 두 가지 파라미터
- epsilon: 입실론으로 표기하는 주변 영역
-> 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역- min points: 이 입실론 주변 영역에 포함되는 최소 데이터의 개수
-> 개별 데이터의 입실론 주변 영역에 포함되는 타 데이터의 개수
입실론 주변 영역 내에 포함되는 최소 데이터 개수를 충족시키는가 아닌가에 따라 데이터 포인트를 다음과 같이 정의
- 핵심 포인트 (Core Point): 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 가지고 있을 경우 해당 데이터
- 이웃 포인트 (Neighbor Point): 주변 영역 내에 위치한 타 데이터
- 경계 포인트 (Border Point): 주변 영역 내에 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지 않지만, 핵심 포인트를 이웃 포인트로 가지고 있는 데이터
- 잡음 포인트 (Noise Point): 최소 데이터 개수 이상의 이웃 포인트를 가지고 있지 않으며, 핵심 포인트도 이웃 포인트로 가지고 있지 않는 데이터
DBSCAN 실습
scikit-learn에서는 sklearn.cluster.DBSCAN 클래스를 지원함
eps: 입실론 주변 영역의 반경
min_samples: 핵심 포인트가 되기 위해 입실론 주변 영역 내에 포함돼야 할 데이터의 최소 개수를 의미함 (자신의 데이터를 포함)
-> 이론에서 설명한 min_points에 +1
iris 데이터 불러오고 데이터프레임으로 만들기
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
iris = load_iris()
feature_names = ['sepal_length','sepal_width','petal_length','petal_width']
irisDF = pd.DataFrame(data=iris.data, columns=feature_names)
irisDF['target'] = iris.target
eps=0.6,min_samples=8설정하고 DBSCAN 군집화 실행
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.6, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)target dbscan_cluster
0 0 49
-1 1
1 1 46
-1 4
2 1 42
-1 8
Name: dbscan_cluster, dtype: int64-1은 어느 군집에도 속하지 못한 Noise를 뜻함
그걸 제외하면 0과 1로 2개의 군집으로 나뉘었음
원래 3개의 Target이 있었지만 우리가 앞에서 봤던 것 처럼
setosa만 혼자 떨어져있고, versicolor와 virginica는 거의 붙어있어서 이렇게 나온 듯
GMM 할 때 만들었던 시각화하는 함수
def visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True):
if iscenter :
centers = clusterobj.cluster_centers_
unique_labels = np.unique(dataframe[label_name].values)
markers=['o', 's', '^', 'x', '*']
isNoise=False
for label in unique_labels:
label_cluster = dataframe[dataframe[label_name]==label]
if label == -1:
cluster_legend = 'Noise'
isNoise=True
else :
cluster_legend = 'Cluster '+str(label)
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], s=70,\
edgecolor='k', marker=markers[label], label=cluster_legend)
if iscenter:
center_x_y = centers[label]
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=250, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',\
edgecolor='k', marker='$%d$' % label)
if isNoise:
legend_loc='upper center'
else: legend_loc='upper right'
plt.legend(loc=legend_loc)
plt.show()시각화를 위해 PCA로 Feature를 2개로 줄이고 시각화
from sklearn.decomposition import PCA
# 2차원으로 시각화하기 위해 PCA n_componets=2로 피처 데이터 세트 변환
pca = PCA(n_components=2, random_state=0)
pca_transformed = pca.fit_transform(iris.data)
# visualize_cluster_2d( ) 함수는 ftr1, ftr2 컬럼을 좌표에 표현하므로 PCA 변환값을 해당 컬럼으로 생성
irisDF['ftr1'] = pca_transformed[:,0]
irisDF['ftr2'] = pca_transformed[:,1]
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)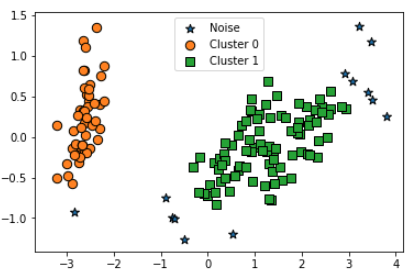
예상대로 versicolor와 virginica가 합쳐져 있고, Noise가 일부 있음
eps를 0.8로 증가시키고 다시 해보자
밀도를 산정하는 범위가 늘어나는 거니까 아마 Noise가 줄어들 것임
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.8, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)target dbscan_cluster
0 0 50
1 1 50
2 1 47
-1 3
Name: dbscan_cluster, dtype: int64
예상대로 Noise가 많이 줄었음 (3개 남음)
이번에는 min_samples의 크기를 증가시키자 주변 영역 최소 데이터 개수를 증가시키니까 아마 Noise가 늘어날 것임
dbscan = DBSCAN(eps=0.6, min_samples=16, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)target dbscan_cluster
0 0 48
-1 2
1 1 44
-1 6
2 1 36
-1 14
Name: dbscan_cluster, dtype: int64
예상대로 Noise가 늘어남
iris는 그만하고, DBSCAN에 더 적합한 데이터로 해보자
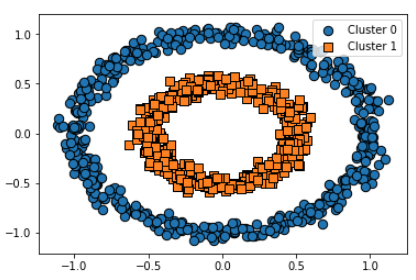
scikit-learn의make_circles로 다음 결과와 같은 데이터를 만듦
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, shuffle=True, noise=0.05, random_state=0, factor=0.5)
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)
비교를 위해, K-Means Clustering 진행
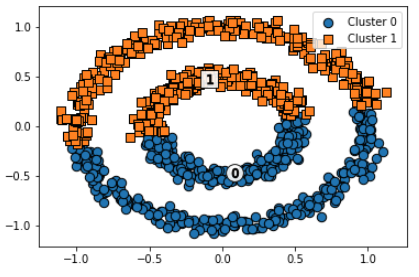
# KMeans로 make_circles( ) 데이터 셋을 클러스터링 수행.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, max_iter=1000, random_state=0)
kmeans_labels = kmeans.fit_predict(X)
clusterDF['kmeans_cluster'] = kmeans_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_cluster', iscenter=True)
제대로 군집화 안 됨
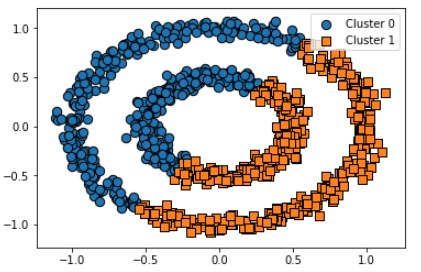
GMM Clustering 진행
# GMM으로 make_circles( ) 데이터 셋을 클러스터링 수행.
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2, random_state=0)
gmm_label = gmm.fit(X).predict(X)
clusterDF['gmm_cluster'] = gmm_label
visualize_cluster_plot(gmm, clusterDF, 'gmm_cluster', iscenter=False)
마찬가지로 제대로 군집화 안 됨
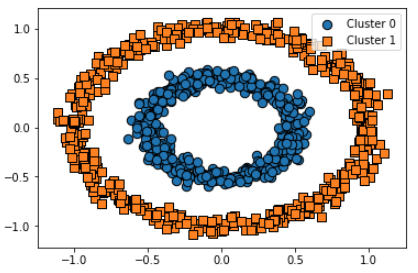
DBSCAN Clustering 진행
# DBSCAN으로 make_circles( ) 데이터 셋을 클러스터링 수행.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=10, metric='euclidean')
dbscan_labels = dbscan.fit_predict(X)
clusterDF['dbscan_cluster'] = dbscan_labels
visualize_cluster_plot(dbscan, clusterDF, 'dbscan_cluster', iscenter=False)
완벽하게 군집화 됨!
