Gaussian Mixture Model, Mixture of Gaussian, GMM, MoG
Gaussian Mixture Model 개요
거리기반 K-Means의 문제점
-> K-Means는 특정 중심점을 기반으로 거리적으로 퍼져있는 데이터 세트에 군집화를 적용하면 효율적인데 그 반대는 비효율적이다.
예를 들어보자
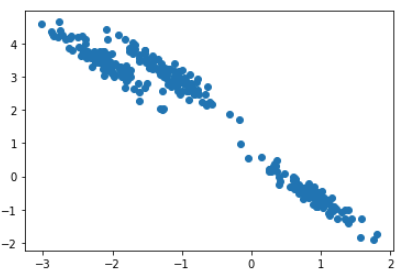 K-Means는 이런 데이터에서 군집화가 제대로 되지 않는다.
K-Means는 이런 데이터에서 군집화가 제대로 되지 않는다.
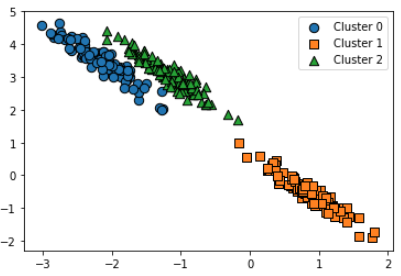
누가봐도 세 개의 군집이 보이는데, 거리 기반의 K-Means는 다음과 같이 군집화한다.
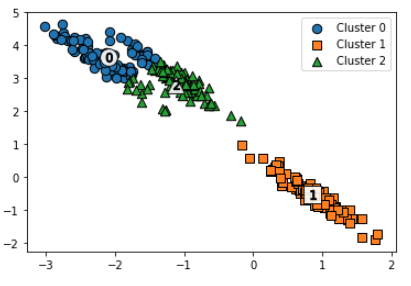 거리 기반으로 이루어지기 때문에 이런 문제가 발생한다.
거리 기반으로 이루어지기 때문에 이런 문제가 발생한다.
GMM으로 해보자
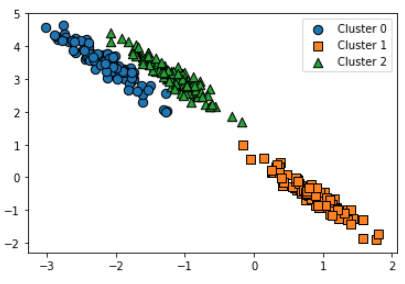 예상대로 한 것과 똑같이 군집화가 됐다.
예상대로 한 것과 똑같이 군집화가 됐다.
그럼 GMM 군집화는 뭘까?
- 군집화를 적용하고자 하는 데이터가 여러 개의 다른 가우시안 분포를 가지는 모델로 가정하고 군집화를 수행
- 가령 1000개의 데이터 세트가 있다면 이를 구성하는 여러 개의 정규분포 곡선을 추출하고, 개별 데이터가 이 중 어떤 정규분포에 속하는지 결정
GMM은 EM 알고리즘을 사용한다. (사실 K-Means도 이걸 사용함)
EM (Expectation and Maximization)
- Expectation
-> 개별 데이터 각각에 대해서 특정 정규 분포에 소속될 확률을 구하고 가장 높은 확률을 가진 정규 분포에 소속
(최초에는 데이터들을 임의로 특정 정규 분포로 소속)- Maximization
-> 데이터들이 특정 정규분포로 소속되면 다시 해당 정규분포의 평균과 분산을 구함
해당 데이터가 발견될 수 있는 가능도를 최대화 (Maximum likelihood) 할 수 있도록 평균과 분산(모수)를 구함
개별 정규분포의 모수인 평균과 분산이 더이상 변경되지 않고
각 개별 데이터들이 이전 정규 분포 소속이 더이상 변경되지 않으면
그것으로 최종 군집화를 결정하고 그렇지 않으면 계속 EM 반복을 수행
-> 이 방법을 수학적으로 설명하면 굉장히 복잡함
Gaussian Mixture Model 실습
scikit-learn은 sklearn.mixture.GaussianMixture 클래스 제공
iris 데이터 불러오고 데이터프레임 만들기
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
iris = load_iris()
feature_names = ['sepal_length','sepal_width','petal_length','petal_width']
irisDF = pd.DataFrame(data=iris.data, columns=feature_names)
irisDF['target'] = iris.targetGMM으로 군집 수 3개로 해서 군집화 진행
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, random_state=0).fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)
# 클러스터링 결과를 irisDF 의 'gmm_cluster' 컬럼명으로 저장
irisDF['gmm_cluster'] = gmm_cluster_labels
# target 값에 따라서 gmm_cluster 값이 어떻게 매핑되었는지 확인.
iris_result = irisDF.groupby(['target'])['gmm_cluster'].value_counts()
print(iris_result)target gmm_cluster
0 0 50
1 2 45
1 5
2 1 50
Name: gmm_cluster, dtype: int64K-Means보다 훨씬 잘 된 거 같음
K-Means로 한 것도 다시 봐보자
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300,random_state=0).fit(iris.data)
kmeans_cluster_labels = kmeans.predict(iris.data)
irisDF['kmeans_cluster'] = kmeans_cluster_labels
iris_result = irisDF.groupby(['target'])['kmeans_cluster'].value_counts()
print(iris_result)target kmeans_cluster
0 1 50
1 0 48
2 2
2 2 36
0 14
Name: kmeans_cluster, dtype: int64클러스터링 결과를 시각화하는 함수를 만듦 (뒤에 DBSCAN에서도 사용)
iscenter인자는 centroid를 표시할지 말지 결정 (GMM은 없음)
### 클러스터 결과를 담은 DataFrame과 사이킷런의 Cluster 객체등을 인자로 받아 클러스터링 결과를 시각화하는 함수
def visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True):
if iscenter :
centers = clusterobj.cluster_centers_
unique_labels = np.unique(dataframe[label_name].values)
markers=['o', 's', '^', 'x', '*']
isNoise=False
for label in unique_labels:
label_cluster = dataframe[dataframe[label_name]==label]
if label == -1:
cluster_legend = 'Noise'
isNoise=True
else :
cluster_legend = 'Cluster '+str(label)
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], s=70,\
edgecolor='k', marker=markers[label], label=cluster_legend)
if iscenter:
center_x_y = centers[label]
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=250, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',\
edgecolor='k', marker='$%d$' % label)
if isNoise:
legend_loc='upper center'
else: legend_loc='upper right'
plt.legend(loc=legend_loc)
plt.show()
make_blobs로 군집 랜덤 표본을 추출하고
GMM에 적합하게 데이터를 비틀음
-> 앞에 개요에서 봤던 그 데이터임
어떻게 군집 표본 추출 되었는지까지 시각화
from sklearn.datasets import make_blobs
# make_blobs() 로 300개의 데이터 셋, 3개의 cluster 셋, cluster_std=0.5 을 만듬.
X, y = make_blobs(n_samples=300, n_features=2, centers=3, cluster_std=0.5, random_state=0)
# 길게 늘어난 타원형의 데이터 셋을 생성하기 위해 변환함.
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
# feature 데이터 셋과 make_blobs( ) 의 y 결과 값을 DataFrame으로 저장
clusterDF = pd.DataFrame(data=X_aniso, columns=['ftr1', 'ftr2'])
clusterDF['target'] = y
# 생성된 데이터 셋을 target 별로 다른 marker 로 표시하여 시각화 함.
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)K-Means 군집화 진행 후 시각화하기
# 3개의 Cluster 기반 Kmeans 를 X_aniso 데이터 셋에 적용
kmeans = KMeans(3, random_state=0)
kmeans_label = kmeans.fit_predict(X_aniso)
clusterDF['kmeans_label'] = kmeans_label
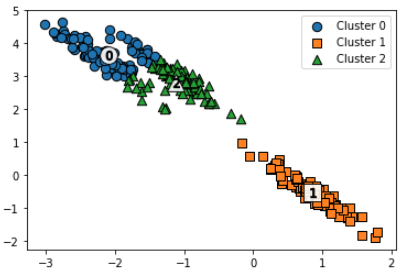
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_label',iscenter=True)거리 기반 특성상 이렇게 군집화가 되어버림
GMM 군집화 진행 후 시각화하기
# 3개의 n_components기반 GMM을 X_aniso 데이터 셋에 적용
gmm = GaussianMixture(n_components=3, random_state=0)
gmm_label = gmm.fit(X_aniso).predict(X_aniso)
clusterDF['gmm_label'] = gmm_label
# GaussianMixture는 cluster_centers_ 속성이 없으므로 iscenter를 False로 설정.
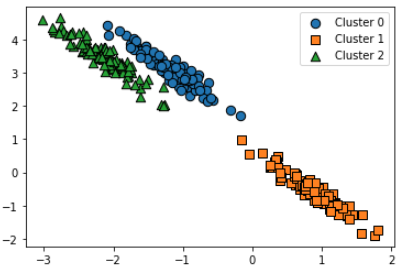
visualize_cluster_plot(gmm, clusterDF, 'gmm_label',iscenter=False)의도한 것과 동일하게 됐음!
둘을 비교해보자
print('### KMeans Clustering ###')
print(clusterDF.groupby('target')['kmeans_label'].value_counts())
print('\n### Gaussian Mixture Clustering ###')
print(clusterDF.groupby('target')['gmm_label'].value_counts())### KMeans Clustering ###
target kmeans_label
0 2 73
0 27
1 1 100
2 0 86
2 14
Name: kmeans_label, dtype: int64
### Gaussian Mixture Clustering ###
target gmm_label
0 2 100
1 1 100
2 0 100
Name: gmm_label, dtype: int64GMM은 의도와 100% 일치하게 군집화 됨!