정밀도와 재현율의 Trade-off 개요
Trade-off: 한 쪽이 높아지면 한 쪽이 낮아짐
정밀도와 재현율이 이런 관계를 가지고 있음
정밀도가 더 중요한 경우
- 실제 Negative 음성인 데이터 예측을 Positive 양성으로 잘못 판단하게 되면 업무 상 큰 영향이 발생하는 경우
- 스팸 메일
재현율이 더 중요한 경우
- 실제 Positive 양성인 데이터 예측을 Negative 음성으로 잘못 판단하게 되면 업무 상 큰 영향이 발생하는 경우
- 암 진단, 금융사기 판별
분류 결정 임곗값이 낮아질수록 Positive로 예측할 확률이 높아짐
- 그러면 재현율이 증가함
- 기본 임계값이 0.5인데 0.5보다 크면 무조건 Positive로 예측
- 0.5보다 작으면 무조건 Negative로 예측
- 근데 임계값을 0.4로 낮추면 Positive로 예측하는 게 더 많아지겠지?
- 그러니까 재현율이 증가함
- 정밀도와 재현율 중에 더 중요한 지표가 무엇인지 판단하고 임계값을 조정!
predict_proba()
scikit-learn의 Estimator 객체의 predict_proba()는 분류 결정 예측 확률을 반환
이를 이용하면 임의로 분류 결정 임곗값을 조정하면서 예측 확률을 변경 가능
predict_proba()했을 때 나오는 값(확률)이 0.5보다 크냐 작냐에 따라
predict()에서 1이냐 0이냐로 구분해준 것임
코드로 이해해보자
앞에서 했던 타이타닉을 LogisticRegression에 적합시킨 것에서 진행함
pred_proba = lr_clf.predict_proba(X_test)
pred = lr_clf.predict(X_test)
print('pred_proba()결과 Shape : {0}'.format(pred_proba.shape))
print('pred_proba array에서 앞 3개만 샘플로 추출 \n:', pred_proba[:3])
# 예측 확률 array 와 예측 결과값 array 를 concatenate 하여 예측 확률과 결과값을 한눈에 확인
pred_proba_result = np.concatenate([pred_proba , pred.reshape(-1,1)],axis=1)
print('두개의 class 중에서 더 큰 확률을 클래스 값으로 예측 \n',pred_proba_result[:3])pred_proba()결과 Shape : (179, 2)
pred_proba array에서 앞 3개만 샘플로 추출
: [[0.4616653 0.5383347 ]
[0.87862763 0.12137237]
[0.87727002 0.12272998]]
두개의 class 중에서 더 큰 확률을 클래스 값으로 예측
[[0.4616653 0.5383347 1. ]
[0.87862763 0.12137237 0. ]
[0.87727002 0.12272998 0. ]]이진 분류라서 열이 2개인 것을 볼 수 있다.
첫 번째 열: 0 (Negative)으로 예측할 확률
두 번째 열: 1 (Positive)로 예측할 확률
- 둘을 합치면 1이 나오는 것을 확인하자
- 0.5를 기준으로
predict()가 예측하는 것을 확인하자
Binarizer
scikit-learn의 Binarizer에서 threshold로 불리는 임곗값을 조정해서 분류를 진행할 수 있다.
간단한 예시를 살펴보자
from sklearn.preprocessing import Binarizer
X = [[ 1, -1, 2],
[ 2, 0, 0],
[ 0, 1.1, 1.2]]
# threshold 기준값보다 같거나 작으면 0을, 크면 1을 반환
binarizer = Binarizer(threshold=1.1)
print(binarizer.fit_transform(X))[[0. 0. 1.]
[1. 0. 0.]
[0. 0. 1.]]1.1보다 큰 값은 1로, 1.1보다 작거나 같은 값은 0으로 분류된 것을 확인
분류 결정 임계값 0.5 기반에서 Binarizer를 이용하여 예측값 변환해보자
predict_proba()의 두 번째 열인 1을 예측하는 확률을 뽑아서,
그것이 0.5보다 큰지 작은지를 Binarizer로 판단하고, 평가하는 것이다.
get_clf_eval()은 앞에서 만든 평가지표들을 출력하는 함수이다.
from sklearn.preprocessing import Binarizer
#Binarizer의 threshold 설정값. 분류 결정 임곗값임.
custom_threshold = 0.5
# predict_proba( ) 반환값의 두번째 컬럼 , 즉 Positive 클래스 컬럼 하나만 추출하여 Binarizer를 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869기본값인
0.5로 지정하니까 앞에서 한 것과 완전히 동일하게 나왔다.
0.4로 바꿔보자
# Binarizer의 threshold 설정값을 0.4로 설정. 즉 분류 결정 임곗값을 0.5에서 0.4로 낮춤
custom_threshold = 0.4
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test , custom_predict)오차 행렬
[[99 19]
[10 51]]
정확도: 0.8380, 정밀도: 0.7286, 재현율: 0.8361임곗값을 낮추니까 정밀도는 낮아지고, 재현율은 높아졌다!
반복문을 이용해서 임곗값 상승에 따른 정밀도와 재현율의 Trade-off를 확인하자
# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장.
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
def get_eval_by_threshold(y_test , pred_proba_c1, thresholds):
# thresholds list객체내의 값을 차례로 iteration하면서 Evaluation 수행.
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print('임곗값:',custom_threshold)
get_clf_eval(y_test , custom_predict)
get_eval_by_threshold(y_test ,pred_proba[:,1].reshape(-1,1), thresholds )임곗값: 0.4
오차 행렬
[[99 19]
[10 51]]
정확도: 0.8380, 정밀도: 0.7286, 재현율: 0.8361
임곗값: 0.45
오차 행렬
[[103 15]
[ 12 49]]
정확도: 0.8492, 정밀도: 0.7656, 재현율: 0.8033
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도: 0.8364, 재현율: 0.7541
임곗값: 0.6
오차 행렬
[[112 6]
[ 16 45]]
정확도: 0.8771, 정밀도: 0.8824, 재현율: 0.7377precision_recall_curve()
scikit-learn에서 임곗값별 정밀도와 재현율을 구하는 함수이다.
precision_recall_curve()는 일반적으로 0.11 ~ 0.95 정도의 임곗값을 담은 ndarray와 이 임곗값에 해당하는 정밀도 및 재현율 값을 담은 ndarray를 반환함
from sklearn.metrics import precision_recall_curve
# 레이블 값이 1일때의 예측 확률을 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
# 실제값 데이터 셋과 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1 )
print('반환된 분류 결정 임곗값 배열의 Shape:', thresholds.shape)
print('반환된 precisions 배열의 Shape:', precisions.shape)
print('반환된 recalls 배열의 Shape:', recalls.shape)
print("thresholds 5 sample:", thresholds[:5])
print("precisions 5 sample:", precisions[:5])
print("recalls 5 sample:", recalls[:5])반환된 분류 결정 임곗값 배열의 Shape: (143,)
반환된 precisions 배열의 Shape: (144,)
반환된 recalls 배열의 Shape: (144,)
thresholds 5 sample: [0.10393302 0.10393523 0.10395998 0.10735757 0.10891579]
precisions 5 sample: [0.38853503 0.38461538 0.38709677 0.38961039 0.38562092]
recalls 5 sample: [1. 0.98360656 0.98360656 0.98360656 0.96721311]다 보기는 힘드니까 15 step 단위로 임곗값에 따른 정밀도와 재현율 값을 확인하자
#반환된 임계값 배열 로우가 147건이므로 샘플로 10건만 추출하되, 임곗값을 15 Step으로 추출.
thr_index = np.arange(0, thresholds.shape[0], 15)
print('샘플 추출을 위한 임계값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))
# 15 step 단위로 추출된 임계값에 따른 정밀도와 재현율 값
print('샘플 임계값별 정밀도: ', np.round(precisions[thr_index], 3))
print('샘플 임계값별 재현율: ', np.round(recalls[thr_index], 3))샘플 추출을 위한 임계값 배열의 index 10개: [ 0 15 30 45 60 75 90 105 120 135]
샘플용 10개의 임곗값: [0.1 0.12 0.14 0.19 0.28 0.4 0.57 0.67 0.82 0.95]
샘플 임계값별 정밀도: [0.389 0.44 0.466 0.539 0.647 0.729 0.836 0.949 0.958 1. ]
샘플 임계값별 재현율: [1. 0.967 0.902 0.902 0.902 0.836 0.754 0.607 0.377 0.148]정밀도와 재현율의 Trade-off 관계가 한눈에 보인다.
아래는 시각화인데 코드 설명은 생략
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test , pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출.
precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
# X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
# threshold 값 X 축의 Scale을 0.1 단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
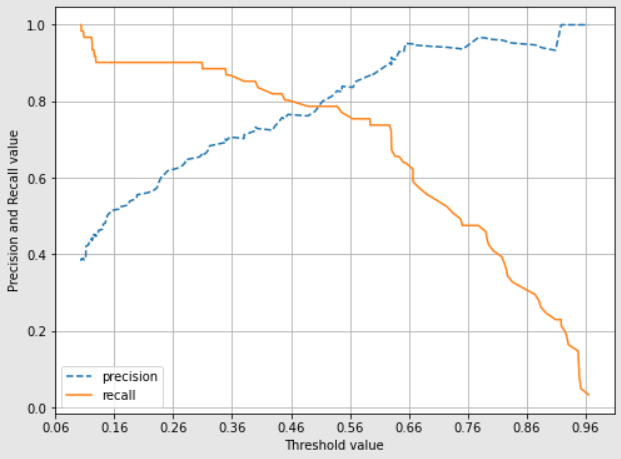
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )정밀도가 높아지니까 재현율이 낮아지는 모습이다.