단순 선형 회귀 (Simple Linear Regression)에 대한 경사 하강법 실습
NumPy로 구현해보기
식 도출 과정은 생략
시뮬레이션 데이터 값 생성
실습을 위해 시뮬레이션 데이터를 생성함
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
X = 2 * np.random.rand(100,1)
y = 6 +4 * X+ np.random.randn(100,1)
plt.scatter(X, y)(Batch) Gradient Descent
과 업데이트시 모든 데이터를 사용하는 Gradient Descent
과 의 값을 최소화 할 수 있도록 업데이트를 수행하는 함수 생성
- zeros_like(W): W와 같은 Shape으로 모든 원소가 0인 ndarray 만듦
- 최종적으로 업데이트된 과 을 반환함
- 나중에 반복문에 들어가서 반복적으로 업데이트 수행
# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update위에서 만든
get_weight_updates()함수를 호출해서 W0과 W1을 반복해서 업데이트하는 함수 생성
- 인자
iters만큼 반복 수행
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0예측 오차 비용 계산을 수행하는 함수 생성
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost경사 하강법 수행 후 최종 값 출력 후 계산
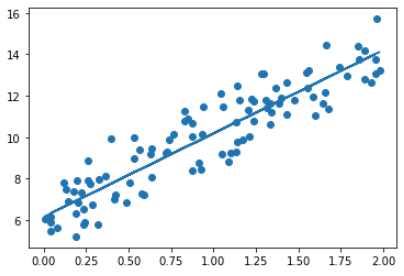
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))w1:4.022 w0:6.162
Gradient Descent Total Cost:0.9935최종 예측한 선형 회귀 선을 그려보기
plt.scatter(X, y)
plt.plot(X,y_pred)Mini-Batch Gradient Descent
과 업데이트시 Batch 사이즈만큼 데이터를 사용하는 Gradient
여기에 설명 있음, 아래 코드는 방법 (1)
get_weight_updates()함수는 Batch것과 같은 것을 사용
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))w1: 4.028 w0: 6.156
Stochastic Gradient Descent Total Cost:0.9937Mini-Batch를 사용해도 Batch와 에 큰 차이가 없음
실제로는 거의 Mini-Batch 방식만 사용함