LinearRegression 클래스 개요
scikit-learn의 LinearRegression 클래스를 알아보자
LinearRegression 클래스
- 예측값과 실제값의 RSS를 최소화하는 OLS 추정 방식으로 구현한 클래스
fit()으로 X, y 배열을 입력 받음- 회귀 계수인 를
coef_에 저장- 절편(bias)은
intercept_에 저장
참고) 다중공선성 (Multicollinearity)
- 일반적으로 선형 회귀는 입력 Feature의 독립성에 많은 영향 받음
- Feature간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 민감해지는 것이 다중공선성
- 일반적으로 상관관계가 높은 Feature가 많은 경우 독립적인 중요한 Feature만 남기고 나머지는 제거하거나 규제 적용
단, Feature를 제거는 일단 그냥 선형 회귀 적용 후 규제 선형 회귀와 비교하고,
회귀 트리하고도 비교하고 나중에 결정!
LinearRegression 클래스 실습
보스톤 주택가격 데이터로 실습 진행
- CRIM: 지역별 범죄 발생률
- ZN: 25,000평방피트를 초과하는 거주 지역의 비율
- INDUS: 비상업 지역 넓이 비율
- CHAS: 찰스강에 대한 더미 변수(강의 경계에 위치한 경우는 1, 아니면 0)
- NOX: 일산화질소 농도
- RM: 거주할 수 있는 방 개수
- AGE: 1940년 이전에 건축된 소유 주택의 비율
- DIS: 5개 주요 고용센터까지의 가중 거리
- RAD: 고속도로 접근 용이도
- TAX: 10,000달러당 재산세율
- PTRATIO: 지역의 교사와 학생 수 비율
- B: 지역의 흑인 거주 비율
- LSTAT: 하위 계층의 비율
- MEDV: 본인 소유의 주택 가격(중앙값)
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_boston
import warnings
warnings.filterwarnings('ignore') # 사이킷런 1.2 부터는 보스턴 주택가격 데이터가 없어진다는 warning 메시지 출력 제거
%matplotlib inline
# boston 데이타셋 로드
boston = load_boston()
# boston 데이타셋 DataFrame 변환
bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names)
# boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가
bostonDF['PRICE'] = boston.target
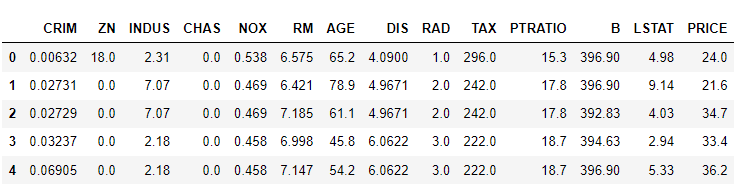
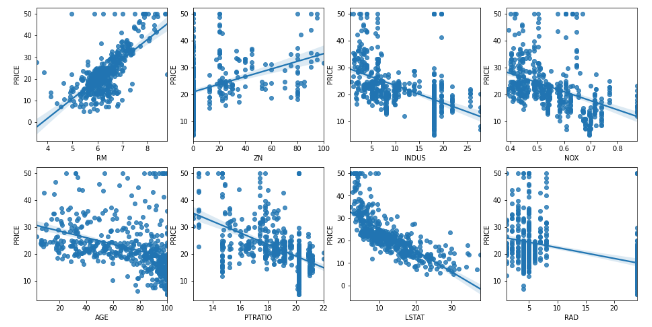
bostonDF.head()Seaborn 라이브러리로 각 Feature가 Price에 미치는 영향을 시각화
# 2개의 행과 4개의 열을 가진 subplots를 이용. axs는 4x2개의 ax를 가짐.
fig, axs = plt.subplots(figsize=(16,8) , ncols=4 , nrows=2)
lm_features = ['RM','ZN','INDUS','NOX','AGE','PTRATIO','LSTAT','RAD']
for i , feature in enumerate(lm_features):
row = int(i/4)
col = i%4
# 시본의 regplot을 이용해 산점도와 선형 회귀 직선을 함께 표현
sns.regplot(x=feature , y='PRICE',data=bostonDF , ax=axs[row][col])RM과 양의 선형관계, LSTAT과 음의 선형관계가 뚜렷함
데이터 분리 후 학습/예측/평가 진행
큰 틀은 분류와 다를 것 없음
RMSE는 mean_squared_error(y_test, y_preds, squared=False)도 가능
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error , r2_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
X_train , X_test , y_train , y_test = train_test_split(X_data , y_target ,test_size=0.3, random_state=156)
lr = LinearRegression()
lr.fit(X_train ,y_train )
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('MSE : {0:.3f} , RMSE : {1:.3F}'.format(mse , rmse))
print('R2 : {0:.3f}'.format(r2_score(y_test, y_preds)))MSE : 17.297 , RMSE : 4.159
R2 : 0.757절편과 회귀계수 출력
print('절편 값:',lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_, 1))절편 값: 40.995595172164336
회귀 계수값: [ -0.1 0.1 0. 3. -19.8 3.4 0. -1.7 0.4 -0. -0.9 0.
-0.6]NOX의 회귀 계수 절댓값이 굉장히 큼
이렇게 단독으로 굉장히 큰 상황은 과적함이 발생할 수 있음을 유의
교차 검증으로 MSE와 RMSE를 다시 구해보자
- 이때 MSE는 scoring에
"neg_mean_squared_error"를 적어야 함- 단, 분류에서 score가 높을수록 좋은데, 회귀에서는 만 제외하면 낮을수록 좋기 때문에 neg가 붙은 것임
- 그래서 저 값은 -1을 곱한 값이 들어감
- 따라서, 제대로 출력하려면 -1을 다시 곱해야함
- 코드를 보면서 이해해보기
from sklearn.model_selection import cross_val_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1,inplace=False)
lr = LinearRegression()
# cross_val_score( )로 5 Fold 셋으로 MSE 를 구한 뒤 이를 기반으로 다시 RMSE 구함.
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv = 5)
rmse_scores = np.sqrt(-1 * neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# cross_val_score(scoring="neg_mean_squared_error")로 반환된 값은 모두 음수
print(' 5 folds 의 개별 Negative MSE scores: ', np.round(neg_mse_scores, 2))
print(' 5 folds 의 개별 RMSE scores : ', np.round(rmse_scores, 2))
print(' 5 folds 의 평균 RMSE : {0:.3f} '.format(avg_rmse))5 folds 의 개별 Negative MSE scores: [-12.46 -26.05 -33.07 -80.76 -33.31]
5 folds 의 개별 RMSE scores : [3.53 5.1 5.75 8.99 5.77]
5 folds 의 평균 RMSE : 5.829 참고) scoring 함수 적용값
- MAE: neg_mean_absolute_error
- MSE: neg_mean_squared_error
- RMSE: neg_root_mean_squared_error
- MSLE: neg_mean_squared_log_error
- R^2: r2