Bike Sharing Demand 데이터
데이터 출처: https://www.kaggle.com/c/bike-sharing-demand
데이터 가공과 사전 작업
칼럼 설명
- datetime: hourly date + timestamp
- season: 1 = 봄, 2 = 여름, 3 = 가을, 4 = 겨울
- holiday: 1 = 토, 일요일의 주말을 제외한 국경일 등의 휴일, 0 = 휴일이 아닌 날
- workingday: 1 = 토, 일요일의 주말 및 휴일이 아닌 주중, 0 = 주말 및 휴일
- weather: 1 = 맑음, 약간 구름 낀 흐림 2 = 안개, 안개 + 흐림 3 = 가벼운 눈, 가벼운 비 + 천둥 4 = 심한 눈/비, 천둥/번개
- temp: 온도(섭씨)
- atemp: 체감온도(섭씨)
- humidity: 상대습도
- windspeed: 풍속
- casual: 사전에 등록되지 않는 사용자가 대여한 횟수
- registered: 사전에 등록된 사용자가 대여한 횟수
- count: 대여 횟수
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore", category=RuntimeWarning)
bike_df = pd.read_csv('./bike_train.csv')
print(bike_df.shape)
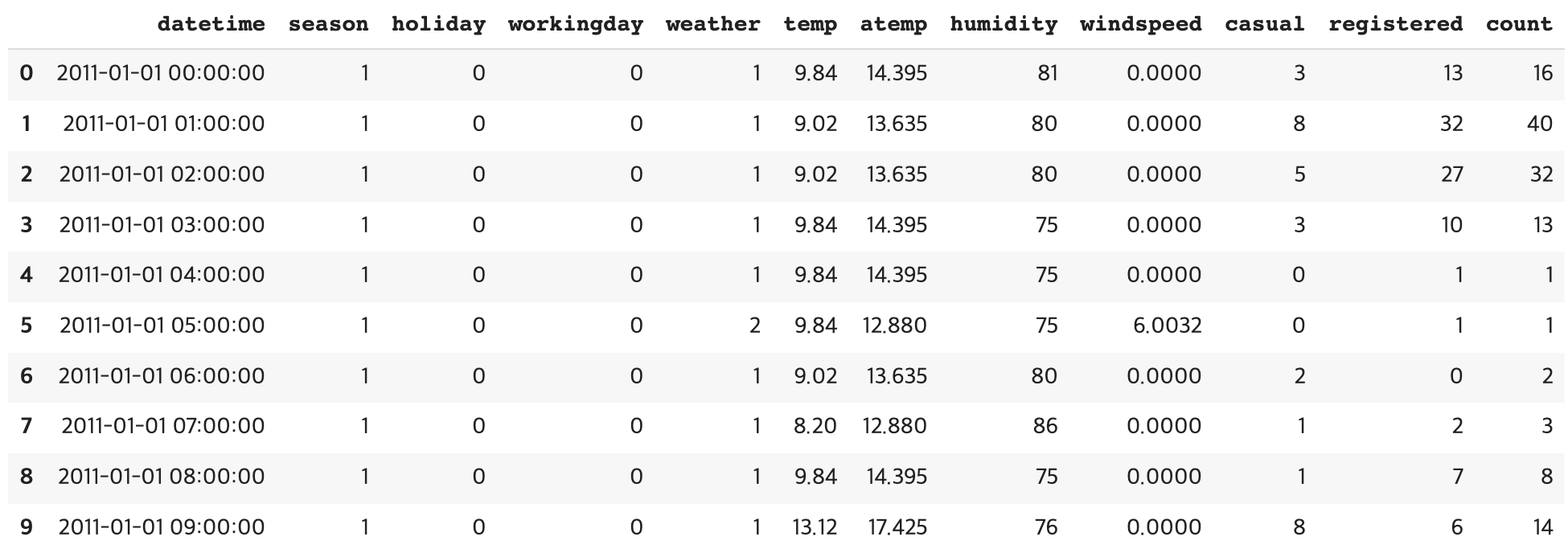
bike_df.head(10)(10886, 12)bike_df.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10886 entries, 0 to 10885
Data columns (total 12 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 datetime 10886 non-null object
1 season 10886 non-null int64
2 holiday 10886 non-null int64
3 workingday 10886 non-null int64
4 weather 10886 non-null int64
5 temp 10886 non-null float64
6 atemp 10886 non-null float64
7 humidity 10886 non-null int64
8 windspeed 10886 non-null float64
9 casual 10886 non-null int64
10 registered 10886 non-null int64
11 count 10886 non-null int64
dtypes: float64(3), int64(8), object(1)
memory usage: 1020.7+ KBdatetime 칼럼이
문자형으로 되어있다.
datetime형으로 변경 후 연/월/일/시간 다 쪼개자
bike_df['datetime'] = bike_df.datetime.apply(pd.to_datetime)
# 연, 월, 일, 시간 추출
bike_df['year'] = bike_df.datetime.apply(lambda x: x.year)
bike_df['month'] = bike_df.datetime.apply(lambda x : x.month)
bike_df['day'] = bike_df.datetime.apply(lambda x : x.day)
bike_df['hour'] = bike_df.datetime.apply(lambda x: x.hour)
bike_df.head(10)이제 불필요한 칼럼을 제거하자
casual와 registered를 더하면 target 칼럼인 count가 되어버린다.
따라서, 예측에 사용하면 안 된다.
datetime 칼럼을 포함해서 세 칼럼 모두 제거하자
drop_columns = ['datetime','casual','registered']
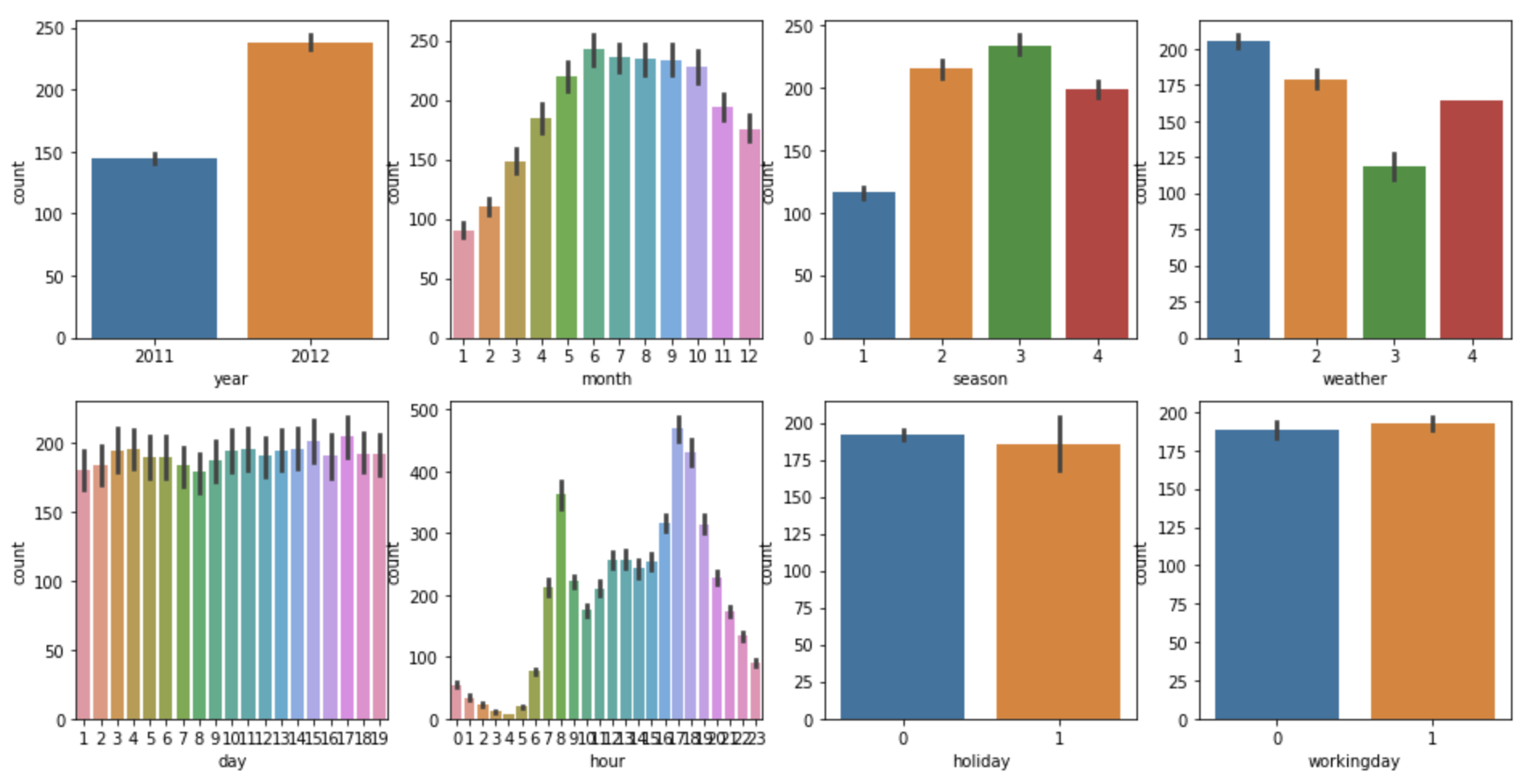
bike_df.drop(drop_columns, axis=1,inplace=True)이제 범주형 Feature에 대해 분포를 시각화해보자
fig, axs = plt.subplots(figsize=(16, 8), ncols=4, nrows=2)
cat_features = ['year', 'month','season','weather','day', 'hour', 'holiday','workingday']
# cat_features에 있는 모든 칼럼별로 개별 칼럼값에 따른 count의 합을 barplot으로 시각화
for i, feature in enumerate(cat_features):
row = int(i/4)
col = i%4
# 시본의 barplot을 이용해 칼럼값에 따른 count의 평균값을 표현
sns.barplot(x=feature, y='count', data=bike_df, ax=axs[row][col])평가지표로는 RMSLE, RMSE, MSE를 사용한다.
RMSLE 식은 다음과 같음
각 평가 지표를 계산하는 함수를 만들어준다.
여기서 log1p, expm1을 사용하는 이유는 값을 방지하기 위함
from sklearn.metrics import mean_squared_error, mean_absolute_error
# log 값 변환 시 NaN등의 이슈로 log() 가 아닌 log1p() 를 이용하여 RMSLE 계산
def rmsle(y, pred):
log_y = np.log1p(y)
log_pred = np.log1p(pred)
squared_error = (log_y - log_pred) ** 2
rmsle = np.sqrt(np.mean(squared_error))
return rmsle
# 사이킷런의 mean_square_error() 를 이용하여 RMSE 계산
def rmse(y,pred):
return np.sqrt(mean_squared_error(y,pred))
# MSE, RMSE, RMSLE 를 모두 계산
def evaluate_regr(y,pred):
rmsle_val = rmsle(y,pred)
rmse_val = rmse(y,pred)
# MAE 는 scikit learn의 mean_absolute_error() 로 계산
mae_val = mean_absolute_error(y,pred)
print('RMSLE: {0:.3f}, RMSE: {1:.3F}, MAE: {2:.3F}'.format(rmsle_val, rmse_val, mae_val))전처리 없이 학습/예측/평가
이 상태에서 Linear Regression으로 학습/예측/평가를 진행해보자
30%를 test 데이터로 쪼갠 후 진행한다.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression , Ridge , Lasso
y_target = bike_df['count']
X_features = bike_df.drop(['count'],axis=1,inplace=False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size=0.3, random_state=0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
evaluate_regr(y_test ,pred)RMSLE: 1.165, RMSE: 140.900, MAE: 105.924지금 나온 평가지표 값들을 확인한 후, 전처리 진행 후 값과 비교해보자
Target값 log 변환 후 학습/예측/평가
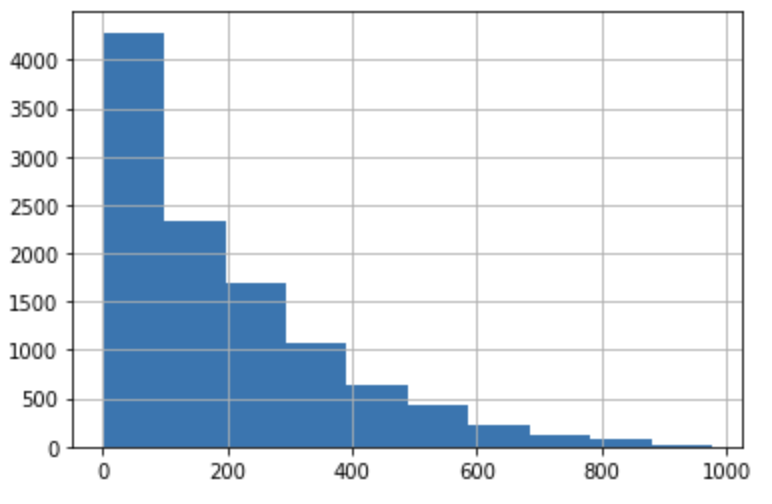
Target 값의 분포를 확인해보자
y_target.hist()Right-skewed 모양이다.
일반적으로 Target 값이 정규분포와 가까워야 성능이 좋게 나온다.
그러기 위해 변환을 진행하자
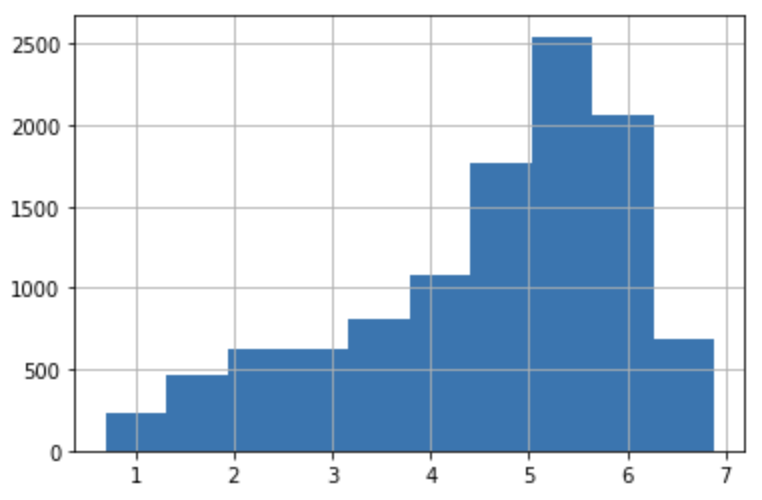
y_log_transform = np.log1p(y_target)
y_log_transform.hist()전보다 정규분포에 가까워졌다. 이 상태에서 학습/예측/평가를 수행해보자
학습/예측 후에는 다시expm1()으로 되돌리고 평가해야 한다!
코드를 잘 보자
# 타깃 칼럼인 count 값을 log1p로 로그 변환
y_target_log = np.log1p(y_target)
# 로그 변환된 y_target_log를 반영하여 학습/테스트 데이터 셋 분할
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target_log, test_size=0.3, random_state=0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
# 테스트 데이터 셋의 Target 값은 Log 변환되었으므로 다시 expm1를 이용하여 원래 scale로 변환
y_test_exp = np.expm1(y_test)
# 예측 값 역시 Log 변환된 타깃 기반으로 학습되어 예측되었으므로 다시 exmpl으로 scale변환
pred_exp = np.expm1(pred)
evaluate_regr(y_test_exp ,pred_exp)RMSLE: 1.017, RMSE: 162.594, MAE: 109.286RMSLE를 빼면 오히려 더 안 좋아졌다.
데이터마다 차이가 있는 것으로 보인다.
(일반적으로는 더 좋아지는게 맞음)
Feature Importance를 확인하자
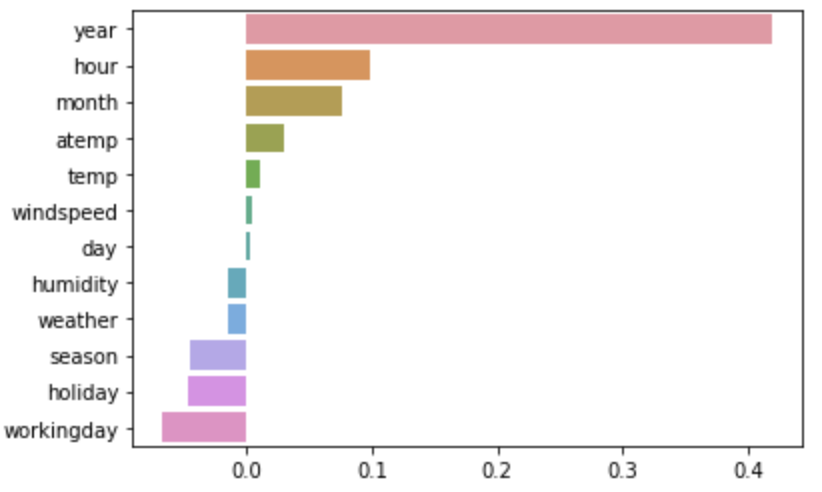
coef = pd.Series(lr_reg.coef_, index=X_features.columns)
coef_sort = coef.sort_values(ascending=False)
sns.barplot(x=coef_sort.values, y=coef_sort.index)날짜 관련 Feature들이 중요하게 나타난다.
원핫인코딩 후 학습/예측/평가
범주형 변수들에 대해
One-Hot Encoding을 수행하자
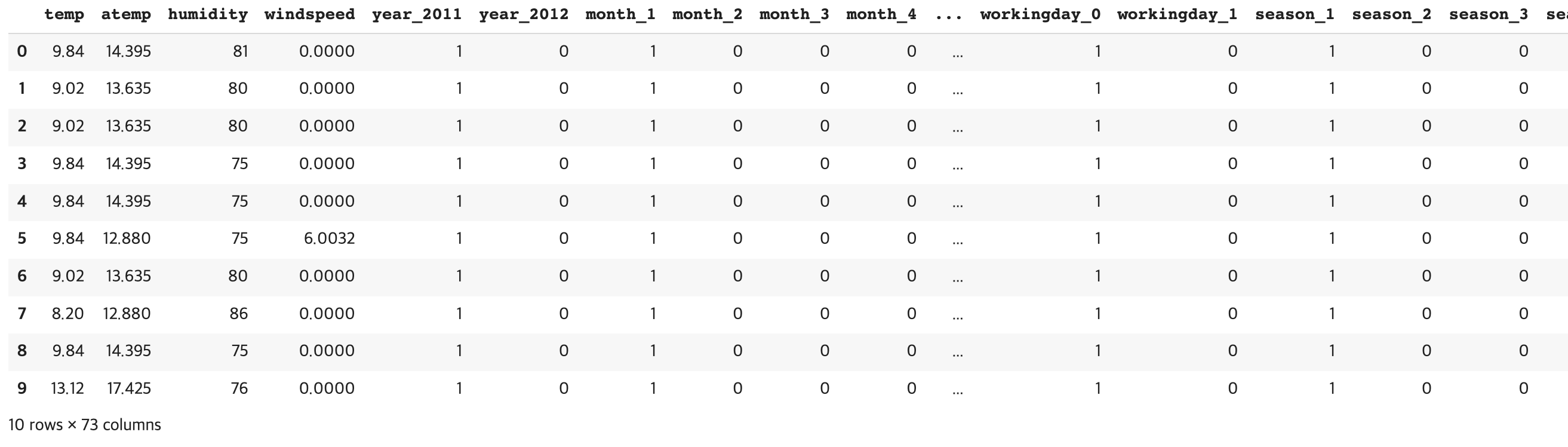
X_features_ohe = pd.get_dummies(X_features, columns=['year', 'month','day', 'hour', 'holiday',
'workingday','season','weather'])
X_features_ohe.head(10)뒤에 좀 잘렸는데, 칼럼이 굉장히 많아짐
이 상태에서 학습/평가/예측을 수행한다.
지금부터는 Linear Regression에 Ridge랑 Lasso까지 포함해서 진행한다.
# 원-핫 인코딩이 적용된 feature 데이터 세트 기반으로 학습/예측 데이터 분할.
X_train, X_test, y_train, y_test = train_test_split(X_features_ohe, y_target_log,
test_size=0.3, random_state=0)
# 모델과 학습/테스트 데이터 셋을 입력하면 성능 평가 수치를 반환
def get_model_predict(model, X_train, X_test, y_train, y_test, is_expm1=False):
model.fit(X_train, y_train)
pred = model.predict(X_test)
if is_expm1 :
y_test = np.expm1(y_test)
pred = np.expm1(pred)
print('###',model.__class__.__name__,'###')
evaluate_regr(y_test, pred)
# end of function get_model_predict
# model 별로 평가 수행
lr_reg = LinearRegression()
ridge_reg = Ridge(alpha=10)
lasso_reg = Lasso(alpha=0.01)
for model in [lr_reg, ridge_reg, lasso_reg]:
get_model_predict(model,X_train, X_test, y_train, y_test,is_expm1=True)
### LinearRegression ###
RMSLE: 0.590, RMSE: 97.688, MAE: 63.382
### Ridge ###
RMSLE: 0.590, RMSE: 98.529, MAE: 63.893
### Lasso ###
RMSLE: 0.635, RMSE: 113.219, MAE: 72.803
오 꽤 많이 좋아졌다.
Tree 계열 Estimator들도 추가해보자
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
# 랜덤 포레스트, GBM, XGBoost, LightGBM model 별로 평가 수행
rf_reg = RandomForestRegressor(n_estimators=500)
gbm_reg = GradientBoostingRegressor(n_estimators=500)
xgb_reg = XGBRegressor(n_estimators=500)
lgbm_reg = LGBMRegressor(n_estimators=500)
for model in [rf_reg, gbm_reg, xgb_reg, lgbm_reg]:
# XGBoost의 경우 DataFrame이 입력 될 경우 버전에 따라 오류 발생 가능. ndarray로 변환.
get_model_predict(model,X_train.values, X_test.values, y_train.values, y_test.values,is_expm1=True)### RandomForestRegressor ###
RMSLE: 0.354, RMSE: 50.238, MAE: 31.116
### GradientBoostingRegressor ###
RMSLE: 0.330, RMSE: 53.330, MAE: 32.740
### XGBRegressor ###
RMSLE: 0.345, RMSE: 58.245, MAE: 35.768
### LGBMRegressor ###
RMSLE: 0.319, RMSE: 47.215, MAE: 29.029역시 요즘 XGBoost와 LightGBM이 핫한 이유가 있다.
성능이 훨씬 더 잘 나온다.
그렇다고 꼭 Tree 계열 회귀가 무조건 성능이 더 좋은 건 아님!
이 데이터는 그렇다는 거고, 선형 회귀 계열이 좋게 나올 수도 있음