파이썬 기초6 - numpy

ganta·2021년 1월 25일

파이썬

파이썬 기초

목록 보기

6/9

이번 포스팅에서는 파이썬의 과학 처리 패키지인 numpy에 대한 내용과 다루는 방법에 대하여 정리를 해 보았습니다.

numpy

왜 numpy를 사용하는가?
- 굉장히 큰 matrix처리 및 다양한 연산 기능 제공
- 반복문 없이 데이터 배열에 대한 처리 지원
- 선형대수와 관련된 다양한 기능 제공
- python은 인터프리터 언어이므로 리스트로 처리 시 속도가 느린 단점이 있다, 넘파이는 이러한 단점을 보완해준다.
- 속도가 빠른 이유
  1, numpy는 C언어로 구현되어 있음
  2, numpy는 한 task를 subtask로 알아서 나눠 병렬적으로 처리한다
  3, 메모리 접근 방식에 대한 차이로 인하여 속도가 빠르다(주소값 저장이 아닌 실제 값을 메모리에 가지고 있어 메모리에 값이 연속적으로 저장되어 있고 이로 인하여 속도가 빠르다.)
  
  출처
  https://checkwhoiam.tistory.com/94
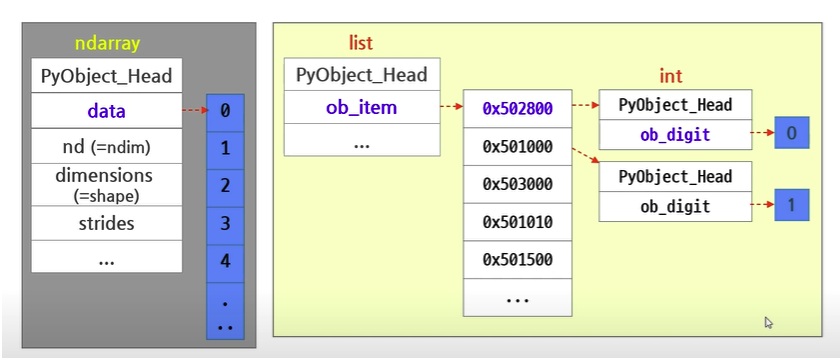
일반 리스트와의 차이
- numpy는 하나의 데이터 타입만 배열에 넣을 수 있다(dynamic typing not supported)
- C언어의 Array를 사용하여 배열을 생성함
- numpy 메모리 구조
  
  출처
  https://www.slideshare.net/enthought/numpy-talk-at-siam

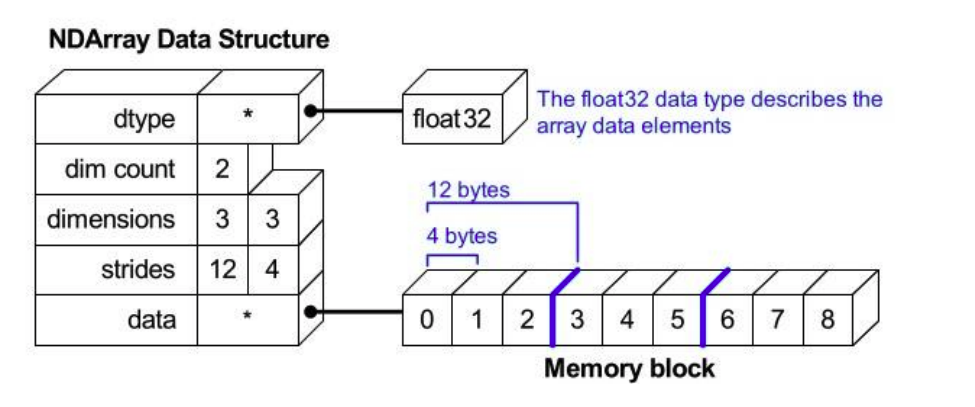
numpy 사용법 및 특징

넘파이 배열 선언 및 인덱스 접근

# 넘파이는 하나의 데이터 타입만 배열에 넣을 수 있음(dynamic typing 지원하지 않음)
m = np.array([1,2,3,4], float)
print(m)
print(m[2]) #3출력

#실수형변환이 가능한 것은 변환이 되어 배열 생성
a = np.array(['1','2',3,4], float)

print(a)
print(type(a[0]))

넘파이는 메모리 직접 값이 들어가기 때문에 같은 정수형 값이라도 "is"구문 이용시 list와는 다른 결과가 나옴

a = [1,2,3,4,5]
b = [1,2,3,4,5]
print(a[0] is b[0]) #True

a = np.array(a)
b = np.array(b)
print(a[0] is b[0]) # False

handling shape

데이터 shape종류
- 0차원 : scalar (7)
- 1차원 : vector ([1,1])
- 2차원 : matrix([1,1],[2,2])
- 3차원 : 3-tensor([[[1,2,3],[4,5,6]] , [[7,8,9], [10,11,12]]])
- n차원 : n-tensor
shape : 차원을 반환, dtype: 데이터 type반환

#scalar
t_arr = np.array([1,2,3,4], float)
print(t_arr.dtype) #float64
print(t_arr.shape)  #(4,)

#matrix
t_arr = np.array([[1,2,3],[4,5,6]], float)
print(t_arr.shape) #(2,3)

#3-tensor
t_arr = np.array([[[1,2,3],[4,5,6]],[[1,2,3],[4,5,6]]], float)
print(t_arr.shape) #(2,2,3)

ndim : 차원의 수, size : 데이터의 개수

t_arr = np.array([[1,2,3],[4,5,6],[4,5,6]], float)
print(t_arr.ndim) #2 (2차원)
print(t_arr.size) #9 (데이터의 갯수)

t_arr = np.array([1,2,3,4], dtype = np.float32) # 32비트로 2진수로 표현
print(type(t_arr[0]))

t_arr = np.array([1,2,3,4], dtype = np.float64) # 64비트로 2진수로 표현
print(type(t_arr[0]))

t_arr = np.array([1,2,3,4], dtype = np.int)
print(type(t_arr[0]))

nbyte : ndarray object의 메모리 크기 반환

t_arr = np.array([1,2,3,4], dtype = np.float32) 
print(t_arr.nbytes) #16 (4*4)

t_arr = np.array([1,2,3,4], dtype = np.float64) 
print(t_arr.nbytes) #32 (8*4)

t_arr = np.array([1,2,3,4], dtype = np.int8)
print(t_arr.nbytes) #4 (1*4)

t_arr = np.array([1], dtype = np.int8) #얼마만큼 메모리 사용하고 있는지(int8은 1바이트)
print(t_arr.nbytes) #1 (1*1)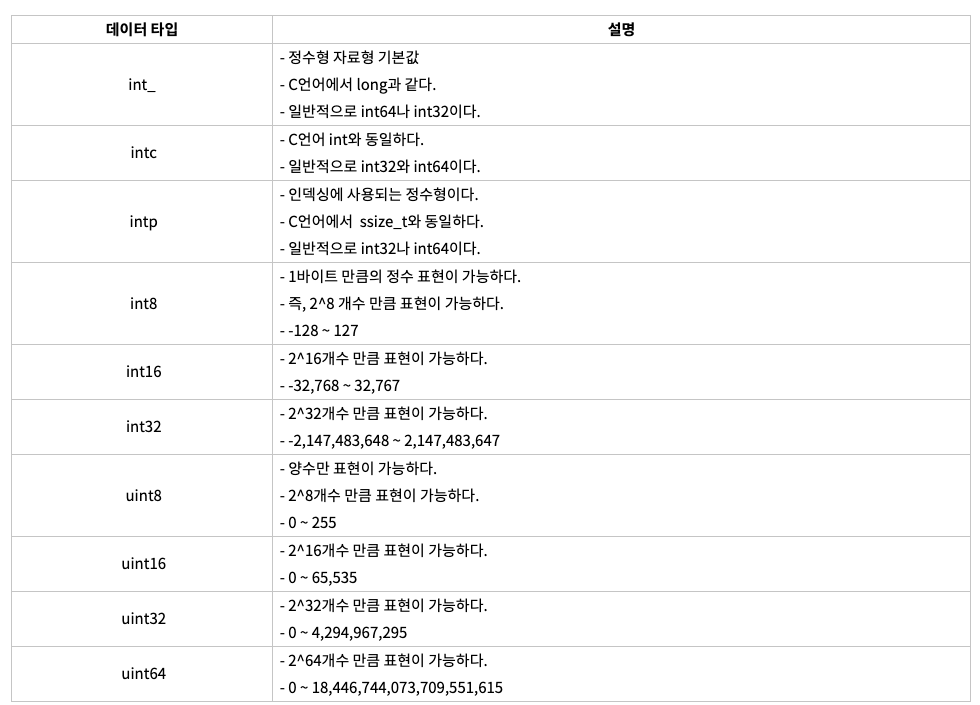

C언어의 자료형과 호환 가능

출처
https://kongdols-room.tistory.com/53

reshape : Array의 shape의 크기를 변경함, element의 갯수는 동일

t_matrix = [[1, 2, 3], [4,5,6]]
np.array(t_matrix).shape

np.array(t_matrix).reshape(3, 2) # 형변환 가능

#-1 : size 기반으로 크기를 알아서 선정해서 reshape해준다.
t_matrix = [[1, 2, 3], [4,5,6]]
print(np.array(t_matrix).reshape(-1, 2)) # 자체 내용이 바뀌지는 않고 return
print("=============")
print(np.array(t_matrix).reshape(3,-1))
print("=============")
print(test_matrix)

t_matrix = [[1, 2, 3,4], [5,6,7,8]]
print("=============")
print(np.array(t_matrix).reshape(1,-1,2))
print(np.array(t_matrix).reshape(1,-1,2).shape)

flatten : 다차원 array를 1차원 array로 변환

test_matrix = np.array([[1, 2, 3,4], [5,6,7,8]])
print(test_matrix.flatten()) #[1 2 3 4 5 6 7 8]
print(test_matrix.flatten().shape) #(8,)
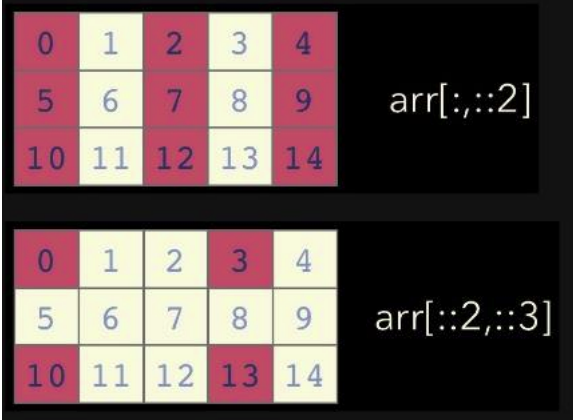
print(test_matrix.flatten().size) #8

indexing & slicing

[0,0]표기법 사용 가능 - list와의 차이점
보다 유연한 슬라이싱 가능

a = np.array([[1,2,3], [4.1,5.1,6.1]], int)

print(a[0,0]) # 1
print(a[0][0]) # 1

# ndarray 값 변환 가능
a[0,0] = 11

a  = np.array([[1,2,3], [4,5,6]], int)

print(a[:,2:])
print("===========")
print(a[:,-1]) #마지막 행 추출
print("===========")
print(a[1,1:3])
print("===========")
print(a[1:3])

출처
https://www.slideshare.net/PyData/introduction-to-numpy

create function

ndarray를 생성하는데 다양하고 유연한 방법들이 존재한다
arange : 범위를 지정하여, 값의 list를 생성하는 명령어

print(np.arange(10))
print(np.arange(0,10,0.6))
print(np.arange(10).reshape(2,5))

zeros : 0으로 가득찬 ndarray생성

print(np.zeros(shape=(10,),dtype = np.int8))
print(np.zeros((2,5)))

ones : 1로 가득찬 ndarray생성

print(np.ones(shape = (10,), dtype = np.int8))
print(np.ones((2,5)))

empty : shape만 주어지고 비어있는 ndarray생성(출력되는 값은 쓰레기값)

print(np.empty(shape=(20,), dtype=np.int8))
print(np.empty((5, 5)))

something_like : 이미 존재하는 ndarray의 shape에 0또는1의 값을 채워 반환
- zeros_like : 0을 채워 반환
- ones_like : 1을 채워 반환

t_matrix = np.arange(30).reshape(5,6)
print(np.ones_like(t_matrix,float))
print(np.zeros_like(t_matrix,float))
print(np.ones_like(t_matrix,int))
print(np.zeros_like(t_matrix,int))

identity : 단위 행렬을 생성함

np.identity(n=3, dtype=np.int8)
np.identity(4)

eye: 대각선이 1인 행렬, k파라미터 이용하여 1이 시작하는 index변경이 가능, 행과 열의 수 지정 가능

print(np.eye(3))
print(np.eye(3,5,k=2))#k는 1의 시작 행을 정함
print(np.eye(N=3, M=5, dtype = np.int8))

diag : 대각 행렬의 값 추출

m = np.arange(9).reshape(3,3)
print(m)
print("========")
print(np.diag(m))

print(m)
print("========")
np.diag(m, k =1)

print(m)
print("========")
np.diag(m, k =0)

print(m)
print("========")
np.diag(m, k =-1)

random sampling
- uniform : 균등분포에 따른 난수 생성
- normal : 정규분포에 따른 난수 생성
- exponential :지수분포에 따른 난수 생성

np.random.uniform(0,1,10).reshape(3,2) #균등분포
np.random.normal(0,1,6).reshape(3,2) # 정규분포
np.random.exponential(scale = 3, size = 10) #지수분포

operation function

sum: ndarray의 element들간의 함을 구함
axis를 이용하여 기준점을 가지고 합을 구할 수 있다.

a = np.arange(11)
print(a.sum())
print(a.sum(dtype = np.float64))

matrix경우
axis = 0 : 행 기준
axis = 1 : 열 기준

a = np.arange(1,11).reshape(2,5)
print(a)
print(a.sum(axis = 0))
print(a.sum(axis = 1))

tensor의 경우

a = np.arange(1,21).reshape(2,5,2)
print(a)

print(a.sum(axis = 0)) #(5,2)
print("=========")
print(a.sum(axis = 1)) #(2,2)
print("=========")
print(a.sum(axis = 2)) #(2,5)

개인적인 tip

만약 3-tensor shape가 (a,b,c) 라고 하면 aixs= 0이면 a를 제거한 (b,c)모양, aixs= 1이면 b를 제거한 (a,c)모양, aixs= 2이면 c를 제거한 (a,b)모양이 되어야 한다. matrix도 마찬가지로 shape가 (a,b) 라고 하면 aixs= 0이면 a를 제거한 (b,)모양, aixs= 1이면 b를 제거한 (a,)모양이 되어야 한다.

mean : 평균, std : 표준편차, sqrt: 제곱근, exp: exponential
이 외에도 다양한 수학 함수들이 존재

m = np.arange(10).reshape(2,5)
print(m)

print(m.mean())
print("==========")
print(m.mean(axis= 0))
print("==========")
print(m.mean(axis= 1))

print(m.std())
print("==========")
print(m.std(axis= 0))
print("==========")
print(m.std(axis= 1))

print(np.sqrt(m))
print("==========")
print(np.exp(m)) #e^m

concatenate : numpy array를 합치는 함수

a = np.array([1,2,3])
b = np.array([2,3,4])
np.vstack((a,b)) #위에서 아래로 쌓임

a = np.array([[1],[2],[3]])
b = np.array([[2],[3],[4]])
np.hstack((a,b)) #왼쪽에서 오른쪽으로 쌓임

concatenate를 axis 기준으로 행렬들을 합칠 수 있다.

a = np.array([[1,2,3]])
b = np.array([[2,3,4]])
np.concatenate((a,b),axis = 0)

a = np.array([[1,2,3]])
b = np.array([[2,3,4]])
np.concatenate((a,b),axis = 1)

a = np.array([[1,2], [3,4]])
b = np.array([[5,6]])
np.concatenate((a,b.T),axis = 1)

차원을 추가하는 2가지 방법
1, reshape()
2, np.newaxis

a = np.array([[1,2], [3,4]])
b = np.array([5,6])

#축을 추가하는 2방법
#1, b.reshape(-1,2)
#2, b = b[np.newaxis,:]
b = b[np.newaxis,:]
np.concatenate((a,b.T),axis = 1)

array operation

기본적인 사칙 연산을 지원

a = np.array([[1,2,3], [4,5,6]], float)
b = np.array([[1,2,3], [4,5,6]], float)

print(a + b)
print(a - b)
print(a * b)

행렬의 곱은 dot함수 혹은 '@'이용

a = np.array([[1,2,3], [4,5,6]], float)
b = np.array([[1,2], [4,5],[5,6]], float)
print(a.dot(b))
print(a @ b)

전치행렬

a = np.arange(10).reshape(2,5)
print(a)
print("=========")
print(a.T)

a = np.arange(20).reshape(2,5,2)
print(a)
print("=========")
print(a.T)

broadcasting: shape이 다른 배열 간 연산을 지원한다.(크기를 늘려 연산을 수행)

m = np.array([[1,2,3], [4,5,6]], float)
scalar = 2

print(m + scalar)
print("============")
print(m - scalar)
print("============")
print(m * scalar)
print("============")
print(m / scalar)

a = np.array([[1,2,3], [4,5,6], [7,8,9]],int)
b = np.array([10,11,12], int)

print(a + b)
print("============")
print(a - b)
print("============")
print(a * b)
print("============")
print(a / b)

timeit : jupyter 환경에서 코드의 퍼포먼스를 체크하는 함수
(일반적으로 속도는 for loop < list comprehension < numpy 순이다.)

%timeit [scalar * value for value in range(1000000)]

%timeit np.arange(1000000) * scalar

comparisions

any : 원소의 일부가 참인 경우 참 반환, all : 원소 모두가 참인 경우 참 반환

a = np.arange(10)

# array([ True,  True,  True,  True, False, False, False, False, False,
#       False])
a < 4

# array([ True, False, False, False, False, False, False, False, False,
#       False])
a < 1

np.all(a < 10) #True
np.all(a < 5) # False
np.any(a < 5) # True
np.any(a > 11) # False

ndarray간의 비교 가능 : boolean type 데이터를 가지는 ndarray반환

a = np.array([1,2,3], float)
b = np.array([4,5,-1], float)

# array([False, False,  True])
a > b

print((a > b).any()) # True
print((a > b).all()) # False

a = np.array([1,2,3], float)
# array([ True,  True, False])
np.logical_and(a>0,a<3)

a = np.array([True,False,False], float)
# array([False,  True,  True])
np.logical_not(a)

c = np.array([False,False,True], float)
# array([ True, False,  True])
np.logical_or(a,c)

where : 조건에 맞는 값 또는 인덱스를 반환

a = np.array([1,2,3], float)
# array([2, 2, 3]) <조건에 맞는 값 반환>
np.where(a>2,3,2)

a = np.arange(10)
# (array([6, 7, 8, 9]),) <인덱스 반환>
np.where(a>5)

a = np.array([1,np.NaN,np.Inf], float)
# array([False,  True, False])
np.isnan(a)# Not a Number

# array([ True, False, False])
np.isfinite(a) # is finite number(유한한 수인가? , 머신러닝 할 경우 발산하는 값을 걸러낼 때 주로 사용)

argmax, argmin : array내 최대값 또는 최소값의 index반환

a = np.array([1,2,3,4,5,6,7,8,9])
print(np.argmax(a)) # 8
print(np.argmin(a)) # 0

a = np.array([[1,7,32],[43,1,4]])
print(np.argmax(a,axis = 1)) # [2 0]
print(np.argmin(a,axis = 0)) # [0 1 1]

argsort : 수를 정렬 한 후 해당 인덱스 뽑아냄

a = np.array([1,2,5,6,7,8,9,4,2,1])
# array([0, 9, 1, 8, 7, 2, 3, 4, 5, 6])
a.argsort()

boolean index & fancy index

boolean index : 특정 조건에 따른 값을 배열 형태로 추출

a = np.array([1,2,5,6,7,8,9,4,2,1])
# array([False, False,  True,  True,  True,  True,  True,  True, False,
#       False])
a > 3

condition = a < 3 #조건은 판단하는 ndarray shape와 동일
a[condition] # array([1, 2, 2, 1])

fancy index : array를 index value로 사용해서 값 추출

a = np.array([2,4,6,8],float)
b = np.array([0,0,1,3,2,1],int) # 반드시 integer로 선언(shape이 같은 필요는 없음)
a[b] #array([2., 2., 4., 8., 6., 4.])

a.take(b) #take 함수 : fancy index와 같은 효과

a = np.array([[1,2], [3,4]], float)
b = np.array([0,1,1,1,0], int)
c = np.array([0,1,1,0,1], int)

print(a)
print("=========")
print(a[b,c])
print("=========")
print(a[b])