RNN

RNN(Recurrent Neural Network)

---

RNN의 기초적인 개념
https://velog.io/@ganta/9-%EA%B8%B0%EC%B4%88-%EC%88%98%ED%95%99-RNN

• LSTM, GRU는 왜 탄생하였는가?
  Vanilla RNN의 모델을 보게 되면 H를 이용하v여 이전 값들에 대한 데이터의 누적 값들을 계속 사용하는 것을 볼 수 있다.이로 인해 여러 문제가 발생하게 된다.
  1, 역전파의 계산시 뜻하지 않은 Gradient의 증폭 혹은 손실이 일어나게 된다.
  2, 순전파의 진행 시 이전 값들이 중첩적으로 활성함수 및 가중치(hyper parameter)와의 연산을 통해서 이전 데이터의 의미가 압축 또는 증폭이 심하게 일어난다.
  (sigmoid 함수 - 계속 값이 압축되어 의미가 사라짐, ReLU 함수 - 양수의 값을 생각해 보았을 때 값이 무한정 커짐 & 음수이면 0이 되어 이전 데이터의 정보가 사라짐 -> 이와 같은 이유 때문에 특히 RNN을 할 때 ReLU활성화 함수를 사용하면 성능이 좋지 않다.)
  위와 같은 이유들 때문에 새로운 network인 LSTM과 GRU같은 모델이 탄생하게 되었다.

LSTM(Long Short Term Memory)

---

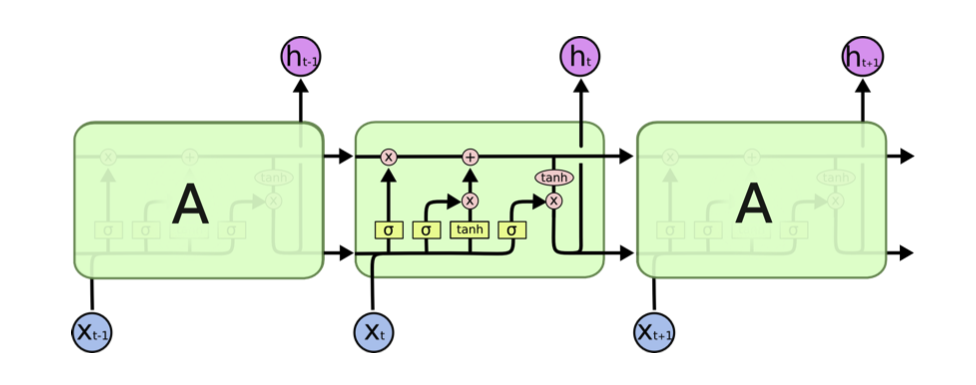
• LSTM은 왜 탄생하게 되었는가?
  Vanila RNN의 한계점이였던 오랜 기간동안 정보를 기억 하기 위해 탄생되었다.
  RNN과 마찬가지로 체인 구조 형태를 가지고 있지만 반복되는 모듈은 Vanila RNN과는 다른 구조를 가지고 있다.

• LSTM의 특징
  1, cell state
  메모리셀 전체 사슬을 관통하고 덧셈 연산으로 구성되어 있어 기울기 증폭, 소실 문제를 해결 할 수 있다.
  
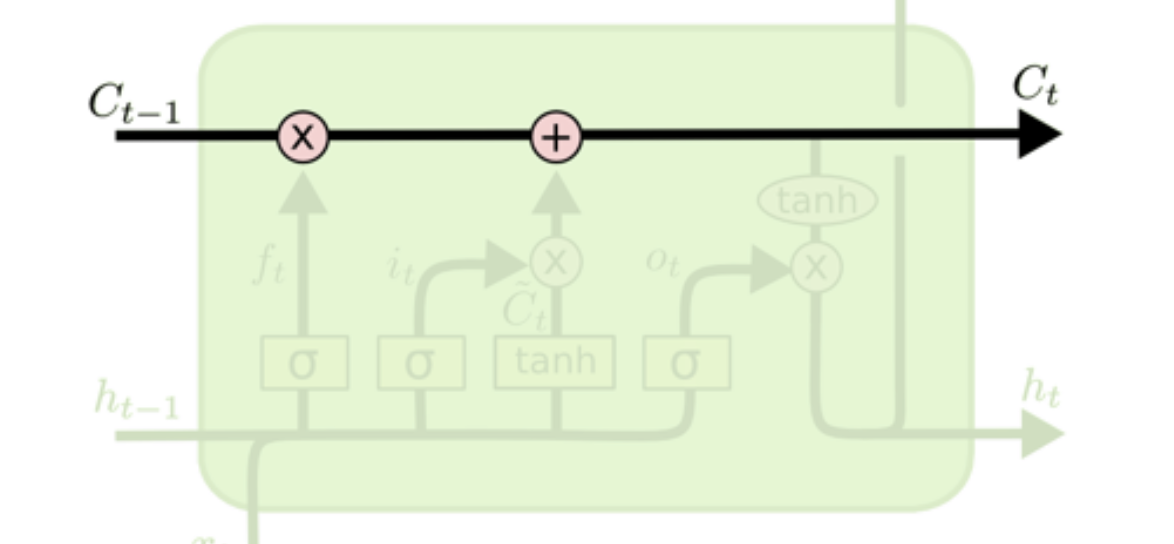
  2, gate
  cell state에 정보를 추가하거나 삭제함으로써 LSTM은 세 개의 게이트를 통해 정보를 통과시킬지 여부를 결정하여 cell state값을 제어한다.
  
  
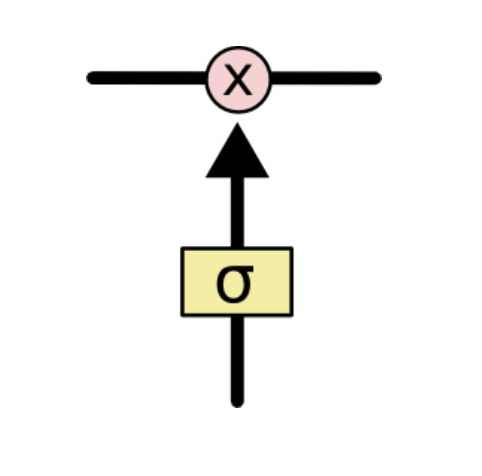
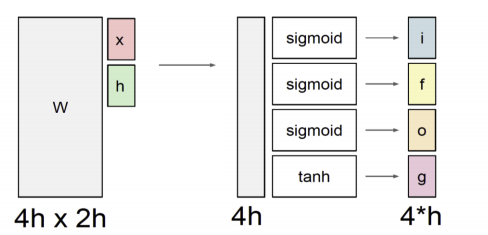
  위의 예시는 x, h의 크기가 각각 h라고 가정 하였을 시 각각의 gate마다의 연산을 그림으로 나타낸 것이며 도출된 게이트의 뜻은 다음과 같다.
  i : input gate
  f : forget gate
  o: output gate
  g : Gate gate

  출처
  Naver BoostCamp AI Tech - edwith 강의

• LSTM의 연산 및 게이트 종류
  1, Forget Gate
  2, Input Gate
  3, Update cell
  4, Output Gate

• Forget Gate
  cell state의 값을 얼마나 버릴지 수치를 제공해 주며 f는 0-1의 값을 가지게 된다.(활성화 함수의 특성 때문)
  
  $\qquad$ $\qquad$ $\qquad$$\qquad$$\qquad$ $f_t = \sigma(W_f \cdot [h_{t-1},x_t] + b_f)$
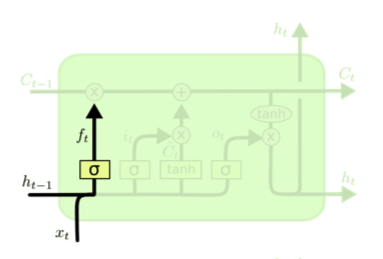
  위의 식을 해석해 보게 되면 이전의 Hidden State와 입력값을 선형변환과 sigmoid함수를 통해 이전 Cell State를 얼마나 반영할 것인지 계산을 진행 해 준다.

  출처
  Naver BoostCamp AI Tech - edwith 강의

• Input Gate, Update cell
  현재 입력을 무작정 올리는 것이 아닌 어떤 입력을 올리고 어떤 입력을 얼마나 올릴지 결정한다. 따라서 틸다C의 값이 모두 올라가는 것이 아니라 일부만 올라간다.
  
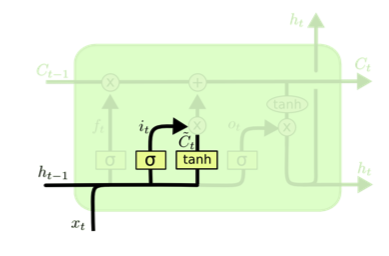
  $\qquad$ $\qquad$$\qquad$$\qquad$$i_t = \sigma(W_i \cdot[h_{t-1},x_t]+b_i)$ => Input Gate
  $\qquad$ $\qquad$$\qquad$$\qquad$$\tilde{C_t} = tanh(W_C \cdot [h_{t-1},x_t] + b_C)$ => update cell(gate gate)
  위의 식을 해석해 보게 되면 기존의 Cell State에서 Hidden State와 입력값을 필요한 정도만 더해주는 식인데 한번의 선형변환만으로 $C_{t-1}$에 더해줘서 값을 update 해 주기가 어려운 경우 일단, 더해주고자 하는 값보다 큰 값으로<$\tilde{C_t}$ (gate gate)>형태로 만들고 특정비율 만큼 정보를 덜어서 Cell State를 만들겠다는 개념이다.

  출처
  Naver BoostCamp AI Tech - edwith 강의

• Output Gate
  cell state와 이전 h의 값을 활용하여 어떤값을 얼마만큼 밖으로 낼지 제어한다.
  
  $\qquad$ $\qquad$ $\qquad$$\qquad$$\qquad$ $o_t = \sigma(W_o \cdot [h_{t-1},x_t] + b_o)$
  $\qquad$ $\qquad$ $\qquad$$\qquad$$\qquad$ $h_t = o_t \cdot tanh(C_t)$
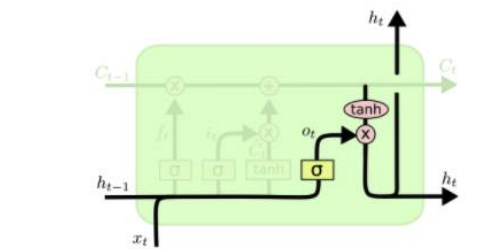
  위의 식을 해석해 보게 되면 Hidden State와 입력값을 선형변환을 취해 준 다음 sigmoid 함수를 통해 output gate를 생성 후 얼마만큼의 정보를 내보낼지(직접적인 필요 정보만을 도출) Cell State에 $tanh$를 통하여 -1 ~ 1의 값으로 변형 한 다음 output gate에 담겨져 있는 필요 비율 정보 만큼 내보내게 되고 이 값은 다음 Cell 의 Hidden state로써 사용이 된다.

  출처
  Naver BoostCamp AI Tech - edwith 강의

• 이러한 과정을 통하여 좀 더 오래전 데이터의 정보를 기억 할 수 있는 모델이 되어 지고(Cell State, Hidden State의 사용) Vanilla RNN보다 보다 정교한 모델이 될 수 있었다.
  에를 들어, 인용문을 적용하고자 할 때 "..." 이러한 문장에서 (")는 서로간 멀리 떨어져 있는 형태가 될 수 있다. 이때, 열었던 (")에 대하여 기억을 하고 있어야 닫는 (")가 나올 수 있기 때문에 이러한 모델은 유용하게 사용이 가능하다.

• 어떻게 Vanilla RNN의 한게점이였던 역전파 문제를 해결 할 수 있었을까?
  전 time step의 Cell State는 필요로 하는 정보를 곱셈이 아닌 덧셈으로 update가 되어지기 때문에 gradient vanishing, gradient explosion문제를 해결 할 수 있었다.

GRU

---

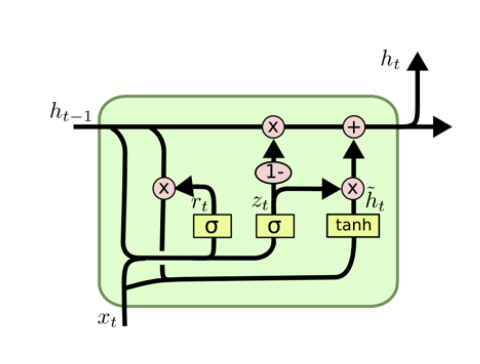
출처
Naver BoostCamp AI Tech - edwith 강의

• LSTM셀의 간소화된 버전이다.

• 네트워크 파라미터가 LSTM보다 상대적으로 적어 어떤 경우에 있어서는 LSTM보다 좋은 성능을 내는 경우가 종종 있다.

• LSTM Cell에서 Cell State(c)와 Hidden State(h)가 h로 합쳐졌다.

• GRU의 게이트 종류
  1, Reset Gate
  2, Update Gate

  • reset Gate
    $\qquad$ $\qquad$ $\qquad$ $r_t = \sigma(W_r \cdot [h_{t-1},x_t])$
    활성화 함수의 결과를 곱해줌으로써 과거의 정보를 얼마만큼 반영하여 입력 정보를 처리 할 것인지 구해준다.(입력 정보 처리 부분 참고)

  • update gate
    $\qquad$ $\qquad$ $\qquad$ $z_t = \sigma(W_z \cdot [h_{t-1},x_t])$
    활성화 함수의 결과를 곱해줌으로써 과거의 정보와 현재의 정보를 얼마나 취할 것인지 구해준다.(출력 값 계산 부분 참고)

  • 입력 정보 처리
    $\qquad$ $\qquad$ $\qquad$ $\tilde h_t = tanh(W\cdot [r _t \cdot h_{t-1},x_t])$
    현시점의 input을 다루기 위한 단계로써 $r_t$,$h_{t-1}$, $x_t$값을 이용하며 값을 도출한다.

  • 출력 값 계산
    $\qquad$ $\qquad$ $\qquad$ $h_t = (1-z_t) \cdot h_{t-1} + z_t \cdot \tilde h_t$
    z는 과거 정보의 일부를 삭제시키면서 현재 정보를 얼마나 취할지 정해줌으로써 이 과정에서 출력값 계산을 한다.
    즉, $z_t$는 input gate, forget gate가 하나의 gate로 수행이 되는 개념이다

• LSTM의 경량화된 모델로써 적은 메모리를 요구하고 빠른 계산 속도를 가지며 어쩔 때는 오히려 성능이 좋을 때도 존재한다.

Transformer

---

• 왜 sequential modeling은 어려운 문제일까?
  입력값이 정직하게 들어올 경우가 있지만 끝 부분, 혹은 중간의 일부분이 생략되어 있는 경우 등 여러 다양한 input에 대하여 유연하게 대처해야 하기 때문이다.
• 입력값에 대한 보다 유연한 처리를 위해 최근에는 Transformer모델을 많이 사용하고 있고 기게어, 이미지 분류, 이미지 detection, 심지어 문장에 맞는 이미지를 띄우는 DALL-E까지 다양한 분야에서 좋은 성능을 보이고 있다.
• 참고 블로그
  https://nlpinkorean.github.io/illustrated-transformer/

Reference

Naver BoostCamp AI Tech - edwith 강의
http://blog.naver.com/PostView.nhn?blogId=apr407&logNo=221237917815&parentCategoryNo=&categoryNo=58&viewDate=&isShowPopularPosts=true&from=search
https://excelsior-cjh.tistory.com/185
https://excelsior-cjh.tistory.com/185
https://m.blog.naver.com/arar2017/221818224142