Generation Model

ganta·2021년 2월 13일

생성 모델

딥러닝 이론

목록 보기

4/17

Unsupervised Learning

Supervised learning : 어느 데이터에 의하여 맞춰야 하는 값이 존재(라벨링이 되어 있음)
- 분류(classification) : 예측하는 값이 카테고리 형식인 것
  예시 - 강아지 종 분류 문제
- 회귀(Regression) : 예측하는 값이 연속적인 것
  예시 - 집값 예측
Unsupervised Learning : 맞춰야 하는 target value(라벨)이 없음
- Clustering : K-means clustering, DBSCAN, SOM 같은 다양한 알고리즘이 존재하고 데이터를 여러 그룹으로 군집화를 수행한다.
- Association Rule (연관 규칙) : 어떤 사건이 얼마나 자주 발생하는지, 서로 얼마나 연관되어 있는지 분석

이번 포스팅에서 다루는 Generation Model은 라벨이 없는 데이터를 가지고 수행하기에 Unsupervised Learning에 해당이 된다.

가능도와 최대 가능도 추정

이산확률 변수의 확률
예를들어, 주사위를 굴려 나올 수 있는 숫자에 대한 확률을 구하고자 하면 각각의 숫자가 나올 확률은 $\frac{1}{6}$ 로 같다. 이때, 숫자가 나오는 경우는 연속적이지 않은 이산적인 변수로써 표현이 되어진다.(1,2,3,4,5,6)
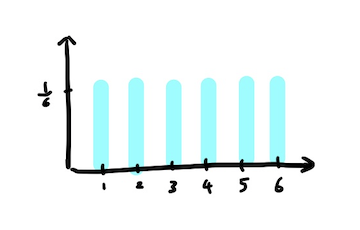
연속확률 변수의 확률
예를들어, 1에서 6사이의 숫자 중 랜덤으로 아무 숫자를 뽑는다 하였을 시 5를 뽑을 확률은 $\frac{1}{\infty}$ 이고 어느 숫자에 대하여도 마찬가지 이다.
연속 사건인 경우 특정 숫자가 나올 확률을 논하는 것은 전부 0이라 의미가 없는데 이에 따라 숫자가 특정 구간에 속할 확률을 다루게 되었고 확률 밀도 함수와 가능도란 개념이 나오게 되었다.
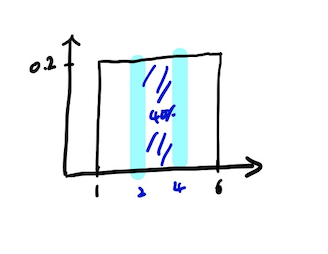
- 특징
  1, 전체 구간에서 확률 밀도 함수를 적분하였을시 전체 확률은 1이 되어야 함으로 넓이는 1이 되어야 한다.
  2, 확률밀도 함수에서 y값을 가능도라 생각하면 된다. y값이 높을수록 일어날 가능성이 높다고 생각하면 된다.
- 최대 가능도 추정량 (Maximum Likelihood Estimator, MLE)
  현재 어떠한 확률 분포인지 알고 있고 어느 특정 해당하는 사건에서 그 사건의 가능도를 최대로 만들 때 그때의 가능도를 추정하는 것을 최대 가능도 추정량 이라고 한다.
  예를 들어, 동전을 1300번 던져 앞면이 900번이 나올 경우를 계산을 해 보았을 때 대략 확률이 0.7일때 가능도가 최대임을 알 수 있다.
  
  Reference
  https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/maximum-likelihood.html
  
  이 말은 즉, 확률 분포를 해당 확률에 대하여 가능도가 되대가 되도록 만드는 것이므로 분포를 결정짓는 파라미터를 특정짓는 것과 같은 말이다.(예를 들어, 가우시안 분포의 경우 평균, 표준편차가 분포를 결정짓기 때문에 최대 가능도를 추정하는 것은 평균과 표준편차를 결정짓는 것과 같다.)

Auto Regressive Model

generation model를 구현 할 때 확률 밀도 함수를 정확하게 아는 경우와 정확하게 모르는 경우 두가지 분류로 나눌 수 있게 되고 그에 따른 다양한 모델들이 존재하게 된다.
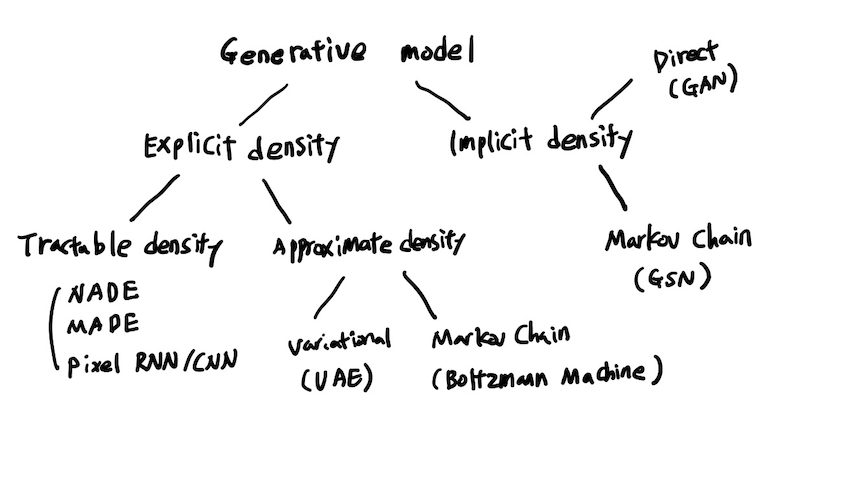
Auto Regressive Model(자가 회귀 모델)이란?
출력 변수가 이전 값에 의존되는 모델이다.
NADE : Neural Autoregressive Density Estimator
explicit 모델로써 확률밀도를 주어진 input값에 의하여 도출하게 됨
예를들어 784 binary pixels에서 가능도를 구하는 식은 다음과 같다.
$p(x_1,...,x_{784}) = p(x_1)p(x_2|x_1)...p(x_784|x_{1:783})$

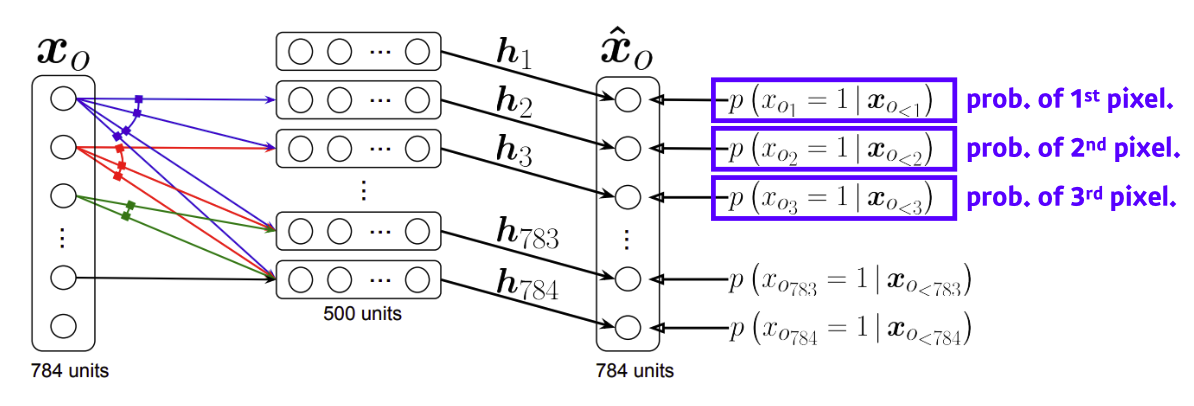
출처
Naver BoostCamp AI Tech - edwith 강의
Pixel RNN
explicit 모델로써 픽셀 하나하나를 sequence로 생각하며 픽셀 하나의 가능도를 산출 할 때 이전 픽셀에 의존하여 가능도를 산출하게 된다.
$p(x) = \prod_{i=1}^{n^2}p(x_{i,R}|x_{<i})p(x_{i,G} | x_{<i},x_{i,R})p(x_{i,B}|x_{<i},x_{i,R},x_{i,G})$
- Pixel RNN에 해당하는 다양한 모델들(ordering of chain에 따라)
  1, Row LSTM
  2, Diagonal BiLSTM
  
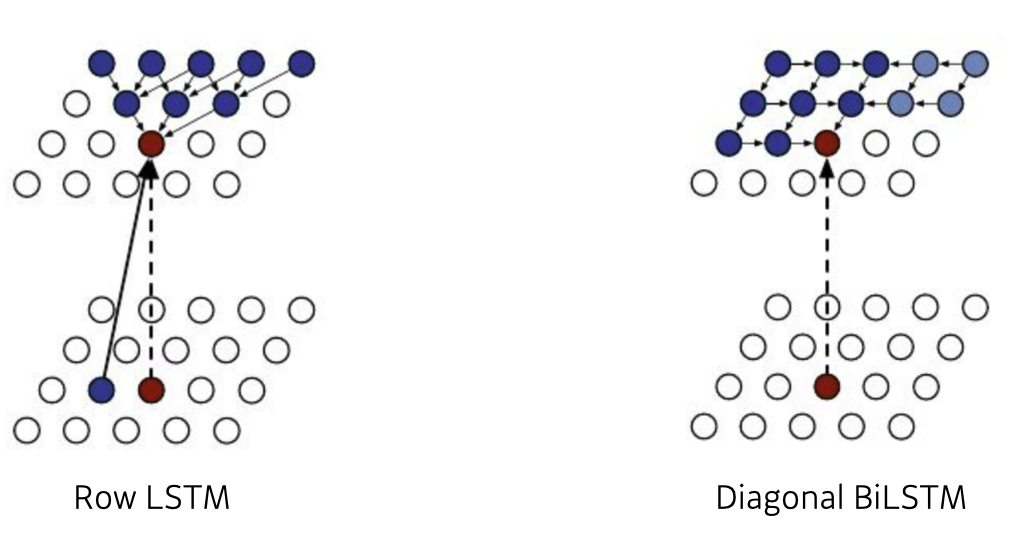
  출처
  Naver BoostCamp AI Tech - edwith 강의

AE VS VAE

Autoencoder(AE)란?
- 단순히 입력을 출력으로 복사하는 신경망으로써 인터더를 통하여 원래의 데이터에서 중요한 특징만을 추출 한 뒤 특징 벡터를 통하여 다시 원래 이미지로 만드는 역활을 수행한다.
- 특별한 라벨이 존재하는 것이 아니기 때문에 unsupervised learning이다.
  
  input 데이터에서 특징 벡터를 뽑아 다시 원래의 input 데이터를 뽑아 내는 것이 목표이다.
  그러면 Autoencoader는 generative model인가?
  결론은 아니다. 그 이유는 새로운 이미지를 만드는 것이 목표가 아닌 원래의 데이터를 복원하는 데에 그 목표가 있기 때문이다.
  이에 비해 Variational Autoencoder는 generative model이다.
Variational Auto-encoder(VAE)란?
- VAE란 AE의 확률모델적 변형으로써 모델로부터 새로운 데이터를 샘플링 할 수 있는 역활을 수행 해 준다.
  
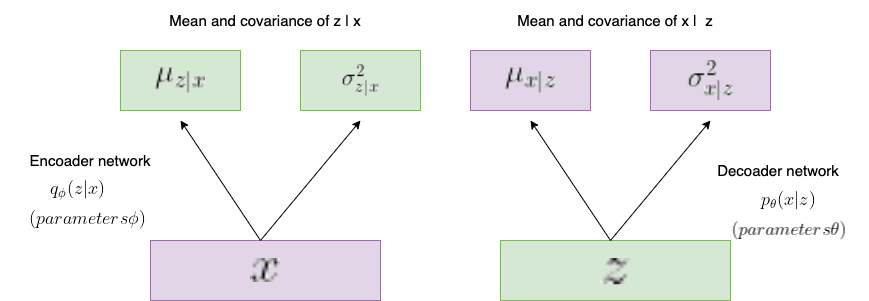
  Encoader 부분에서 input data로 부터 z의 최대 가능도 추정(Maximum Likelihood Estimator)으로 가우시안 분포를 뽑아내도록 한다.(이때, 사실 z는 가우시안 분포를 따르지 않을 수 있지만 가우시안 분포를 따른다고 가정한다.)
  Decoader 부분에서 만들어 낸 가우시안 분포에서 특징벡터 z를 sampling한 다음 이 특징 벡터로부터 x의 최대 가능도 추정(Maximum Likelihood Estimator)으로 가우시안 분포를 뽑아내도록 한다.(이때도 사실 x는 가우시안 분포를 따르지 않을 수 있지만 가우시안 분포를 따른다고 가정한다.)
  이렇게 나온 가우시안 분포에서 sampling을 하여 output 데이터를 가져오도록 한다.(예를 들어, 이미지의 경우 하나의 픽셀마다 가우시안 분포를 이용하여 픽셀 값을 정해 이미지를 뽑아낸다.)
- output data의 가능도를 구하는 공식은 다음과 같다.
  
  우리는 이 가능도를 직접적으로 구할 수는 없지만 식을 유도하여 간접적으로 가능도를 올릴 수 있다. 이를 유도하는 식은 다음과 같다.
  
  lower bound의 값을 올리게 되면 최종적으로 output의 가능도가 올라가게 되고 이 값을 올리기 위해 gradient ascendent로써 학습을 진행을 하게 된다.(알 수 없는 값의 부분은 $D_{KL}$ 의 정의에 의해 항상 양수의 값을 유지한다.)

Generative Adversarial Network(GAN)

GAN이란?
VAE와는 다르게 분포를 가정하지 않고 생성자와 식별자가 서로 경쟁(Adversarial)하며 데이터를 생성(Generative)하는 모델(Network)이다.

이때, Generator Network는 Discriminator Network를 좀 더 잘 속이기 위해 완벽한 가짜 이미지를 만들도록 training 되어지고 Discriminator Network는 가짜 이미지를 더욱 잘 판별하도록 학습이 되어진다.
object function(loss function)

이때, Discriminator는 $D(X)$ 를 1에 가까운 수로 만들도록 하고(진짜 데이터를 넣었을 시) $D(G(Z))$ 를 0에 가까운 수로 만들도록(가짜 데이터를 넣었을 시) 하게 학습을 시킨다.
Generator는 $D(G(Z))$ 를 1에 가까운 수로 만들도록 학습을 시키도록 한다.

Generator학습 시 한가지 문제점이 있는데 초기 학습이 그래프의 모양으로 인하여 잘 이뤄지지 않는 단점이 있다.
따라서, 약간의 함수 변형을 한 다음 학습 진행을 수행하는 테크닉을 사용한다.
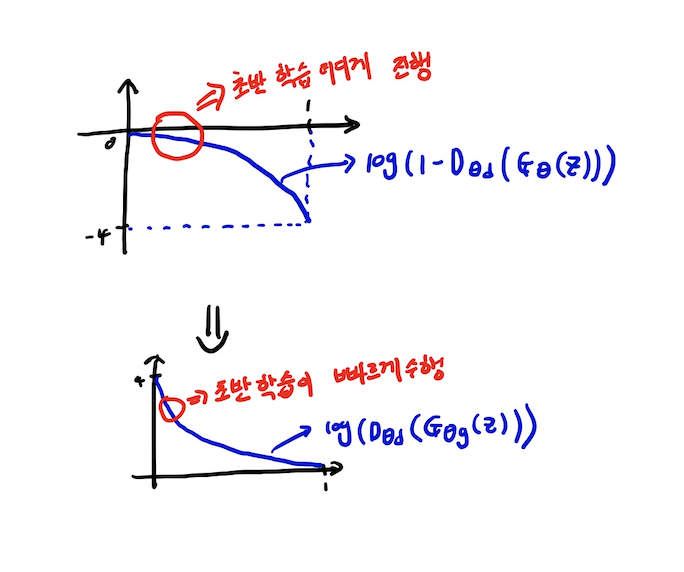
이미지를 다루는 GAN에 있어서 MLP방식 말고 CNN기법을 사용해보자는 DCGAN이 있는데 이 기법에서 주목해야 할 point는 원래 CNN에서 연산을 진행 할 시 보통은 이미지의 크기가 작아지거나 padding을 주워 유지하는 정도의 수준인데 CNN의 역연산 같은 기법을 사용하여 벡터의 크기를 오히려 늘리는 방향으로 연산을 수행하게 된다.

출처
Naver BoostCamp AI Tech - edwith 강의
이외에도 다양한 GAN논문들에 의한 기법들이 나오고 있다.
해당 페이지에 논문에 대한 코드 구현이 있다.
https://github.com/hindupuravinash/the-gan-zoo