신경망 연산 이론
-
신경망에서의 가중치 W를 이용하여 연산을 진행하는 것은 다음 행렬 식과 같다.
(이때, X를 입력값, O를 출력값이라 생각)

출처
Naver BoostCamp AI Tech - edwith 강의해당 식을 노드의 관계로 표현해 보면 다음과 같다.
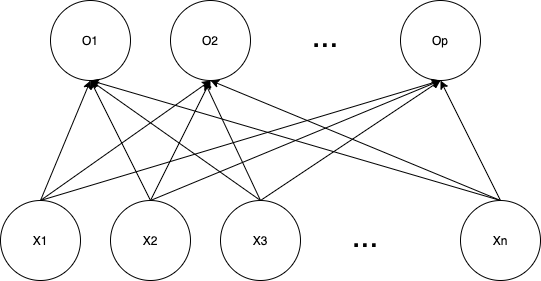
(이때, 전체 간선의 갯수는 d(x의 열 갯수) * d(w의 행 갯수) * n(x의 행 갯수) 이다.)
데이터 정규화 및 전처리
- 정규화 : 데이터를 특정 범위로 변환하는 처리
- 전처리 : 입력 데이터에 특정 변화는 것
- 소프트맥스 함수
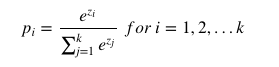
-
결과값의 총합을 1로 만들어 확률로써 어느 클래스로 구분이 될지 판단하게 해 준다.
-
가장 큰 값을 가진 인덱스가 분류된 결과를 가리킨다(one hot 벡터 표현 방식)
- one hot 벡터
만약, 분류 기준이 4개 중 2번 분류 기준에 속해 있다면 [0,1,0,0]으로 표현
- one hot 벡터
-
소프트 맥스는 지수승으로 표현되기에 연산시 오버플로우가 발생 할 수 있는데 분자, 분모에 전처리를 하기전의 데이터 중 가장 큰 수를 나눠 값을 작게 해 준 다음 연산을 진행한다.
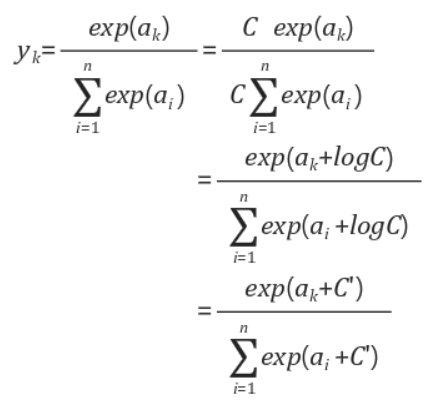
이때 C오버플로우를 막기 위한 수로써 보통 입력된 X(K)에서 가장 큰 수의 마이너스를 곱한 값을 곱한 수이다.
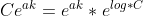
이를 이용하여 소프트맥스를 소스코드 형태로 보이면 다음과 같다.
-
# keepdims - True : 1차원의 배열로 합 반환
# axis= -1 : shape의 가장 오른쪽 차원을 제거 - (1,2,3) => (1,2)
def softmax(vec):
denumerator = np.exp(vec - np.max(vec, axis= -1, keepdims = True))
numerator = np.sum(denumerator, axis = -1, keepdims = True)
val = denumerator / numerator
return val#결과를 one hot 인코딩 형식으로 바꿈
def one_hot(val, dim):
return [np.eye(dim)[_] for _ in val]
def one_hot_encoding(vec):
vec_dim = vec.shape[1]
vec_argmax = np.argmax(vec, axis = -1)
return one_hot(vec_argmax, vec_dim)활성함수
-
활성함와 소프트맥스 함수의 차이
소프트맥스 함수는 벡터 전체에 적용되는 함수라면 활성화함수는 각각의 원소에 값을 변환시키는 것이다. -
선형함수는 층을 아무리 깊이 하여도 의미가 없음
ex) f(x) = ax 일때, f(f(x)) = a a x 이고 이는 a^2 * 로 다시 선형함수가 되기 때문
따라서, 활성함수를 이용하여 비선형 함수를 만들고 사용 -
활성함수의 종류
-
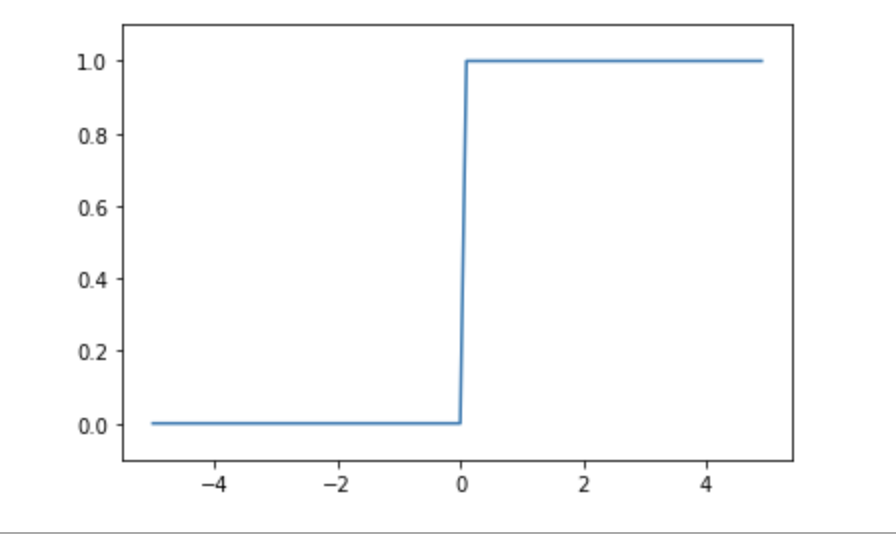
계단함수
- x의 값이 0보다 작으면 0, 0보다 크면 1의 값
- 임게값을 경계로 값이 변환이 됨(연속적이지 않음), 이로 인하여 값에 대하여 답의 유망한 정도의 파악이 유연하지 못하다.(예를 들어 1보다 2가 어느 분류 속성에 더 유망한 답이라 하여도 출력은 1값으로 같다.) - 이로 인한 퍼셉트론의 확장 버전으로 신경망 개념이 나옴
-
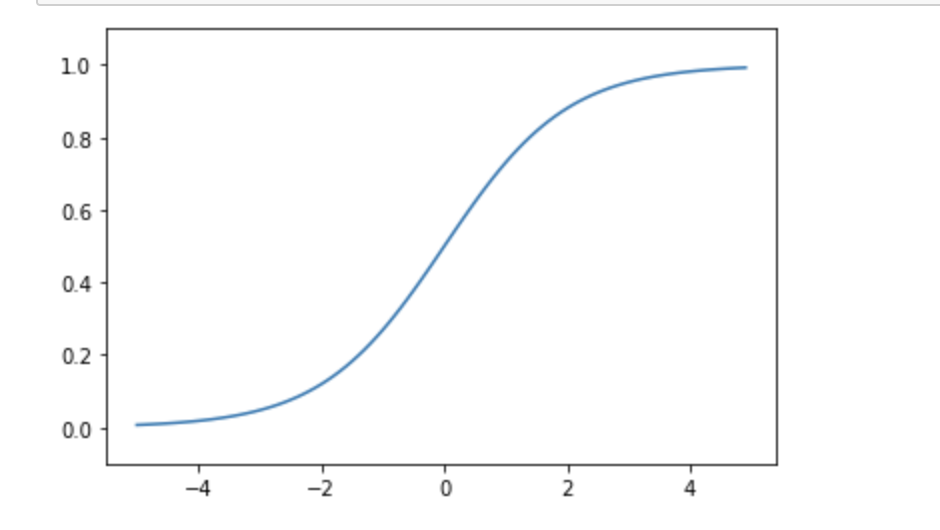
시그모이드 함수
- 0과 1의 사이에서 x값에 따라 다른 값의 실수값을 반환
- 계단함수보다 매끄러움으로 결과값의 정확도를 향상 시킬 수 있음
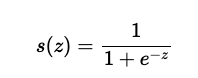
-
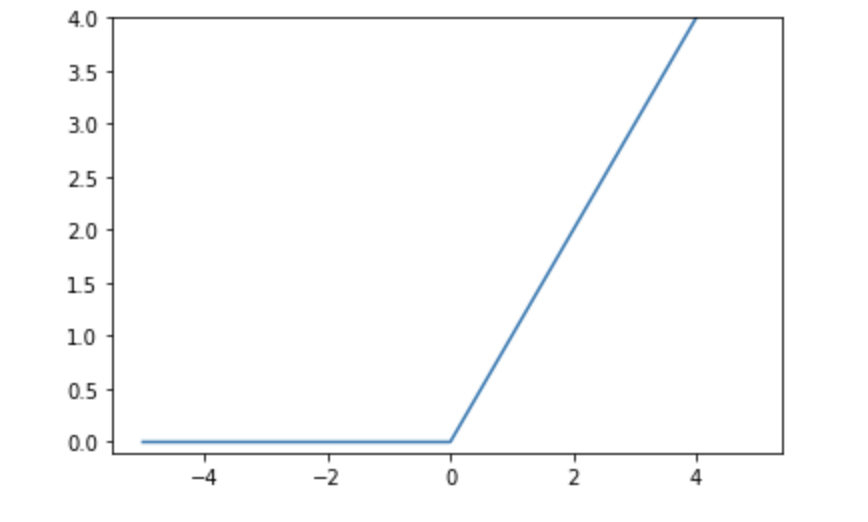
ReLU함수
- 최근 시그모이드 함수 대신 많이 사용하는 활성화 함수
- 0을 넘으면 그 입력을 출력하고, 0 이하이면 0을 출력하는 함수
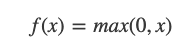
-
hyperbolic tangent

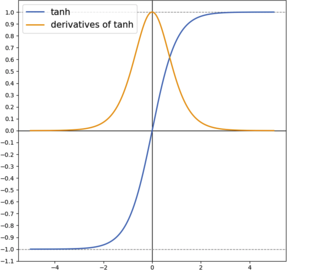
-
-
신경망은 선형모델과 활성함수를 합성한 함수이다.
순전파와 역전파
-
다층퍼셉트론이란?
신경망이 여러층 합성된 함수
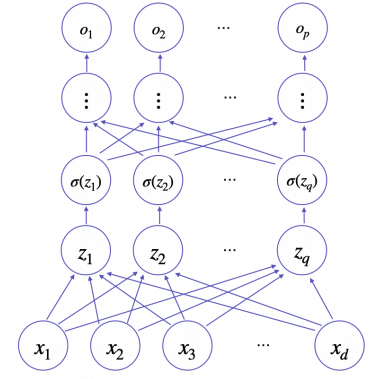
출처
Naver BoostCamp AI Tech - edwith 강의 -
이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있으나 층이 깊을수록 목적함수를 근사하는데 필요한 노드의 수가 훨씬 빨리 줄어들어 좀 더 효율적으로 학습이 가능
-
순전파란?(forward propagation)
- 뉴럴 네트워크 모델의 입력층부터 출력층까지 순서대로 변수들을 계산하고 저장하는 방법을 순전파라 한다.
-
역전파란?(back propagation)
-
뉴럴 네트워크 모델에서 파라미터에 대한 그래디언트를 계산하는 방법
-
아래부터 그래디언트 벡터를 구하기 위해서는 변수에 대한 정보가 없음으로 역순으로 구하게 된다. 따라서, 각 층의 파라미터 그래디언트 벡터는 윗층부터 역순으로 계산하게 된다.(Chain Rule적용)
-
역전파를 하기 위해서는 Chain Rule을 사용하므로 각각의 변수값들은 tensor에 저장이 되어 있어야 한다.(메모리 공간에 저장이 되어 있어야 한다.)

가장 목표가 되는 지점에서 변화율을 구하고자 하는 기준점까지 연관관계를 잊고자 한다면 이와 같이 Chain Rule을 이용하여 추적하여 그 값을 구할 수 있다.
-
Reference
Naver BoostCamp AI Tech - edwith 강의
사이토 고키(齋藤 康毅), 『Deep Learning from Scratch』, 개앞맵시, 한빛미디어(2017), p63-p106
https://www.youtube.com/watch?v=573EZkzfnZ0&list=PLlMkM4tgfjnLSOjrEJN31gZATbcj_MpUm&index=27
https://ko.d2l.ai/chapter_deep-learning-basics/backprop.html
