CNN VS Neural Network
-
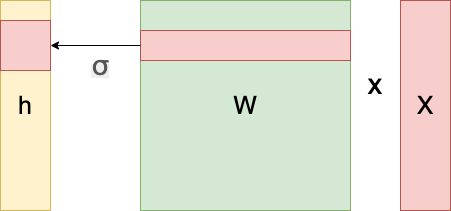
Neural Network의 연산 과정
.gif)
- 각 성분 h(i)에 대응하는 가중치 행 W(i)이 필요하다.
- 즉, 각 뉴런들이 선형모델과 활성함수로 연결된 구조(fully connected)
- 분류 기준이 많아지고 입력 데이터의 성분(x1, x2 ... 즉,차원이 늘어나는 경우)이 많아질 수록 W의 크기는 점점 더 커지게 된다.
-
Convolution Neural Network
.png)
.gif)
- 신경망 연산과 달리 커널(kernel)을 input vector상에서 움직이면서 선형모델과 합성모델이 적용되는 구조
- 모든 i에 대하여 적용되는 커널은 V로 같고 커널의 사이즈만큼 x상에서 이동하며 적용이 된다.
- Neural Network와는 다르게 필요한 hyper parameter의 수가 적은 것을 확인 할 수 있다.(효율적)
Convolution Neural Network
- convolution 연산의 수식적 표현
- 정의역이 연속일 때
.gif)
- 정의역이 이산적일 때
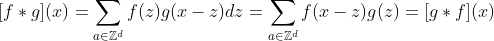
- 해당 식에서 f(z),g(x - z)는 커널과 신호를 뜻하며 z를 움직여가며 값을 바꿔주며 값을 도출 해 나가는 것을 볼 수 있다(이때, f와 g의 역활은 바뀔 수 있으므로 수식에서 확인 할 수 있다.)
- 정의역이 연속일 때
- cross-correlation 연산의 수식적 표현
- 정의역이 연속일 때
.gif)
- 정의역이 이산적일 때
.gif)
- convolution 연산은 z를 빼주면서 값을 도출 해 나갔다면 cross-correlation은 z를 더해주며 값을 도출
=>사실 cnn에서의 연산은 cross-correlation이지만 통상적으로 convolution연산으로 불려 왔기에 Convolution Neural Network(CNN)라고 불리게 되었다.
- 정의역이 연속일 때
- convolution, cross-correlation는 신호를 커널을 이용하여 국소적으로 증폭 혹은 감소하여 정보를 추출 혹은 필터링을 하게 된다.
다양한 차원에서의 convolution 연산
-
convolution연산은 다양한 차원에서 계산이 가능하다.
-
1 demension
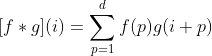
-
2 demension
.gif)
-
3 demension
.gif)
-
-
2 demension상에서의 Convolution연산 과정
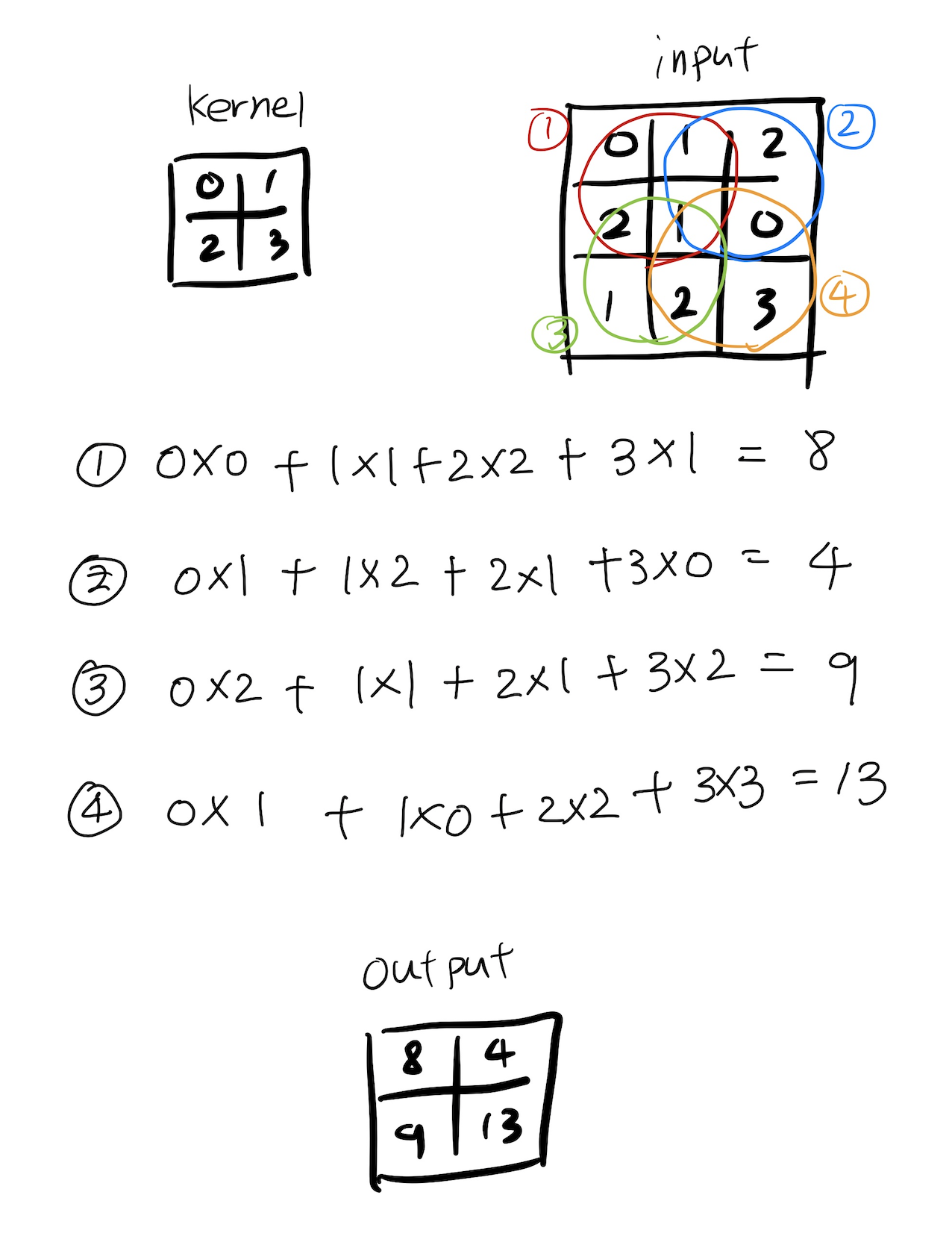
입력 크기를(H,W), 커널 크기를(K(H), K(W)), 출력 크기를(O(H), O(W))라 하였을 때 출력의 크기는 다음과 같다.
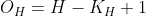
.gif)
-
3 demension상에서의 Convolution연산 과정
.png)

입력 크기를(C,H,W), 커널 크기를(C, K(H), K(W))라 하였을 때 출력의 크기는 (1,O(H), O(W))이다.만약, 입력 커널의 수가 C개면 다음과 같다.
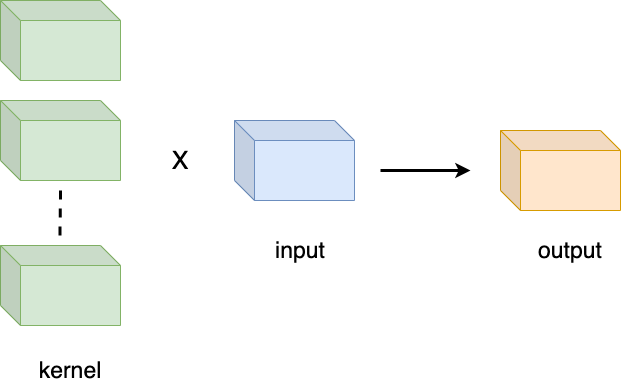
입력 크기를(H,W,C), 커널 크기를(K(H), K(W), C)라 하고 커널의 수를 C개라 하면 출력의 크기는 (O(H), O(W), C)이다.
Convolution 연산의 역전파
-
convolution 연산은 커널이 모든 입력데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.
-
convolution 연산의 역전파의 수식
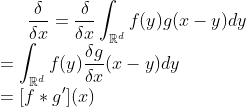
-
convolution 연산의 역전파 예시로 이해하기
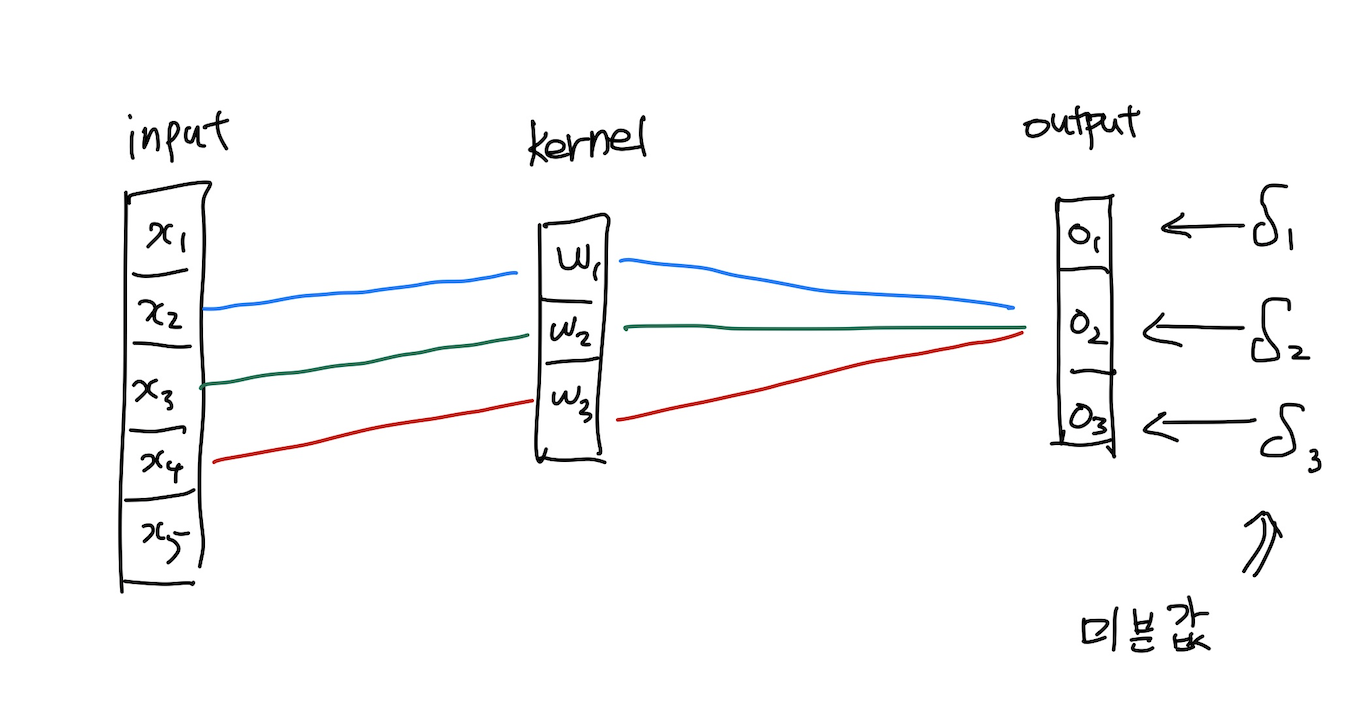
위와 같은 convolution의 연산이 주워져 있다고 생각하자
kernel은 input상에서 움직이면서 각각의 output을 도출을 하게 된다.
(이때, stride를 1을 주게 되면 총 3번을 움직이게 되어 output이 3개가 도출이 된다.)
이에 따라 식을 도출해 보게 되면 다음과 같다.
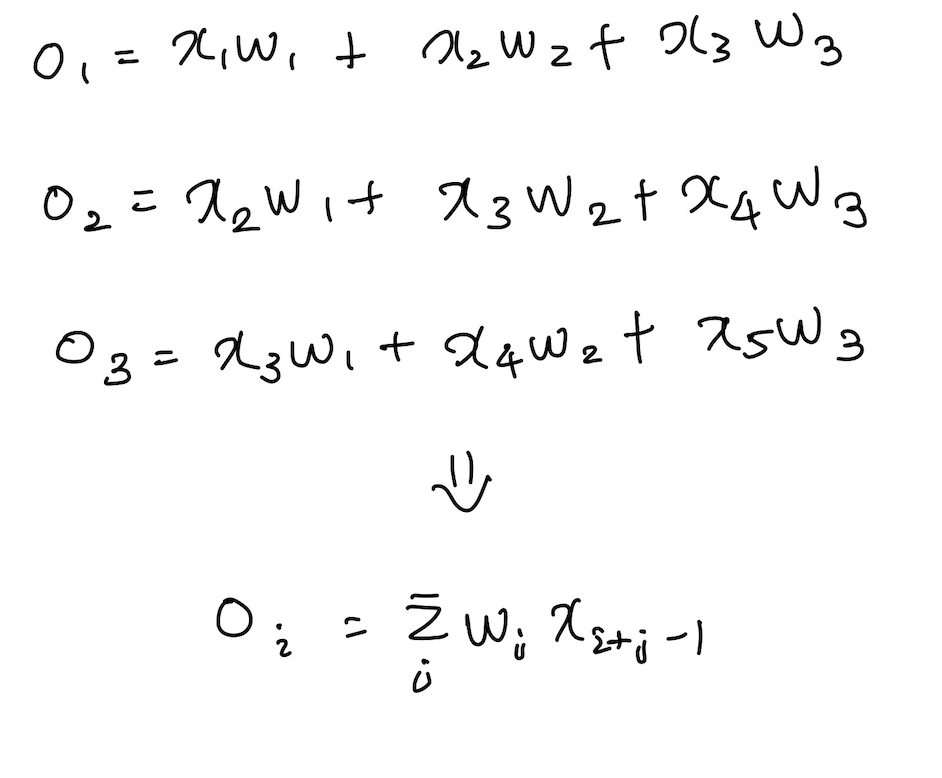
이때, 컨볼루션 층에 전체 손실에 대한 편미분값인 (δ1, δ2, δ3)이 역전파 되었으므로 이를 Chain rule을 통하여 w1, w2, w3에 대한 편미분 값을 구할 수 있다. convolution층의 마지막 도출이 되는 값을 L로 두고 식을 세워나가 보면 다음과 같다.

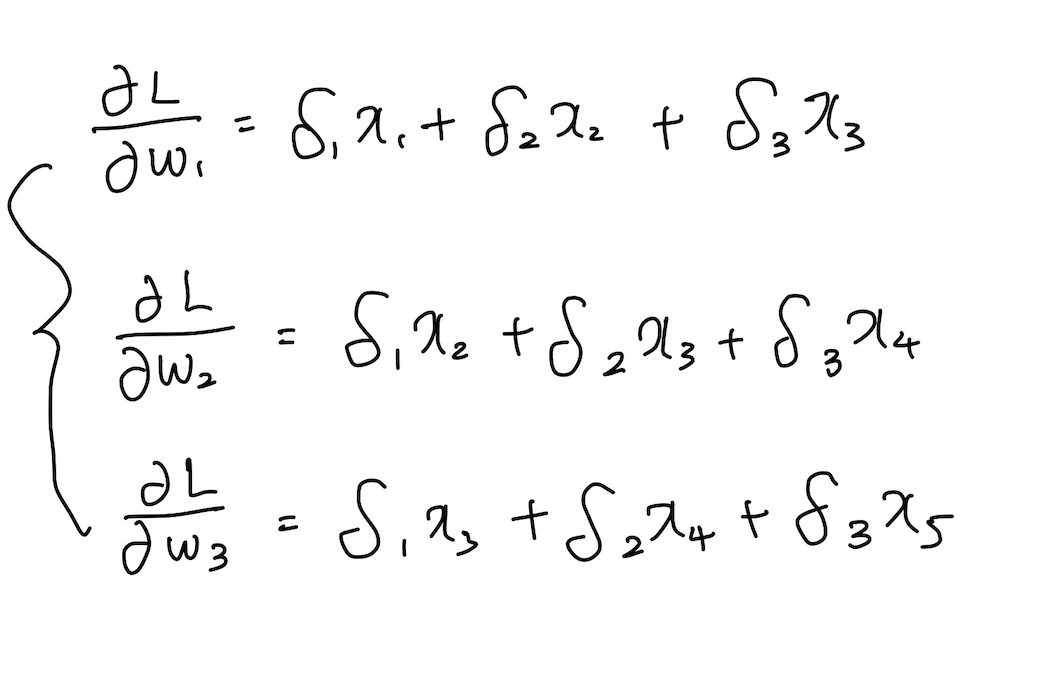
즉, 위와 같은 형태로써 미분된 (δ1, δ2, δ3)값으로 convolution연산을 해 준 형태와 같은 형태가 나오는 것을 볼 수 있다.
Reference
Naver BoostCamp AI Tech - edwith 강의
