Word의 벡터화

ganta·2021년 2월 15일

NLP

딥러닝 이론

목록 보기

5/17

Bag of Words

Bag of words란?
단어의 순서는 고려하지 않고, 단어들의 출현 빈도에만 집중하는 텍스트 데이터의 수치화 표현방법
Bag of Words의 표현 방법
1, 문장의 단어들을 unique하게 모은 다음 사전 형식으로 관리한다.

출처: Naver BoostCamp AI Tech - edwith 강의

2, 각각의 단어들을 one hot 벡터 형식으로 표현한다.
Bag of words의 한계
1) 각각의 단어마다 거리는 $\sqrt{2}$ 으로 일정하다.
2) 유사도는 0으로 일정하다.

출처: Naver BoostCamp AI Tech - edwith 강의

3, 문장이나 문서는 one hot vector의 합으로써 표현이 된다.

출처: Naver BoostCamp AI Tech - edwith 강의
NaiveBayes Classifier
어느 문서 혹은 문장이 존재하고 클래스 분류가 존재 할 때 Bag of Words를 이용하여 어느 분류에 속할 지 판단 할 수 있다.
d 는 document(문장)이고 c는 class라 할 시 다음을 만족하는 것을 찾아냄

출처: Naver BoostCamp AI Tech - edwith 강의
$P(d|c)P(c)$ 의 식을 풀어 써보면 다음과 같다.
$P(d|c)P(c) = P(w_1,w_2,...,w_n | c)P(x) \rightarrow P(c)\prod_{w_i\in W}P(w_i|c)$
이때, $w$ 는 각각의 단어들을 지칭하는데 각각의 단어가 나올 사건은 독립사건이기 때문에 곱셈으로 식을 변환하여 판단 할 수 있다.
확률론적으로 접근하는 방법으로써 단어가 한번도 나오지 않은 부분에 있어서는 0이 나올 수 있음으로 이를 방지하기 위한 여러가지 regularization(스무딩) 같은 기법들을 사용하여 해결을 진행
확률 계산 예시

출처: Naver BoostCamp AI Tech - edwith 강의

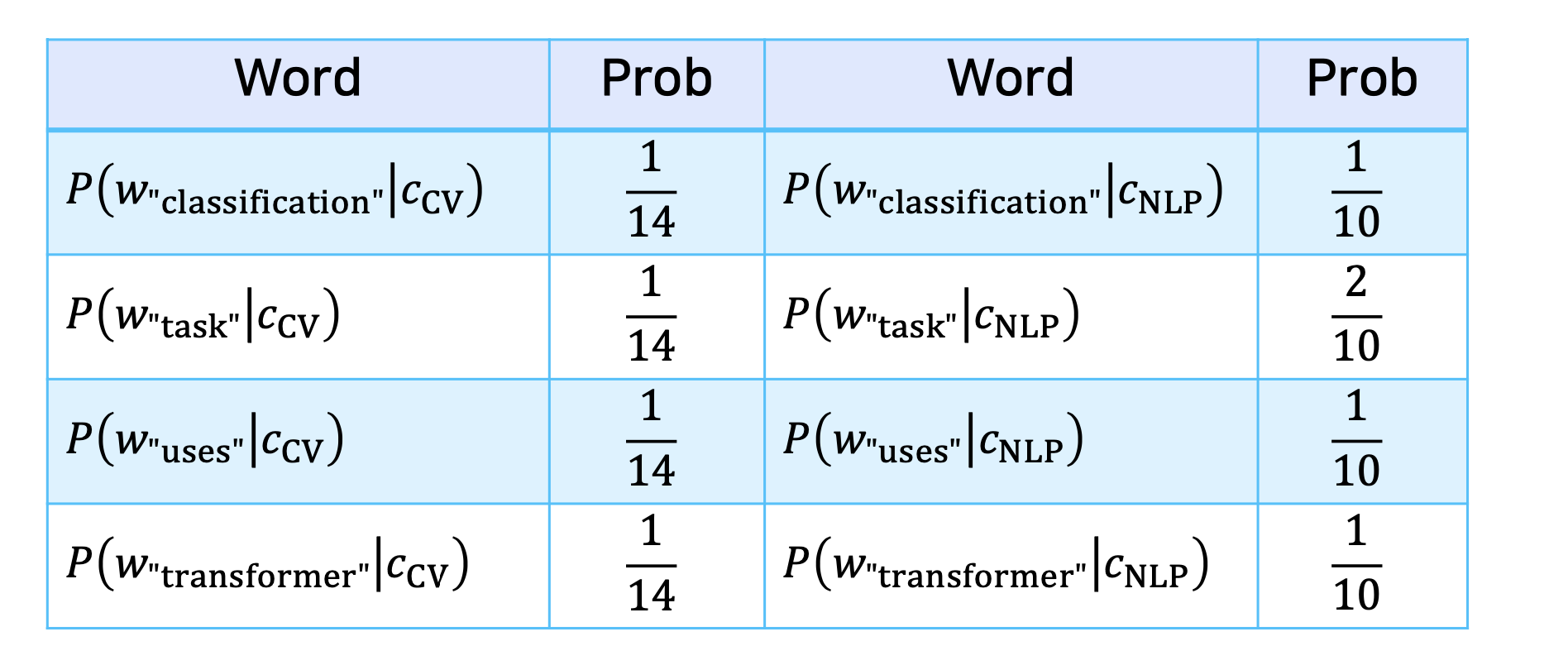
출처: Naver BoostCamp AI Tech - edwith 강의

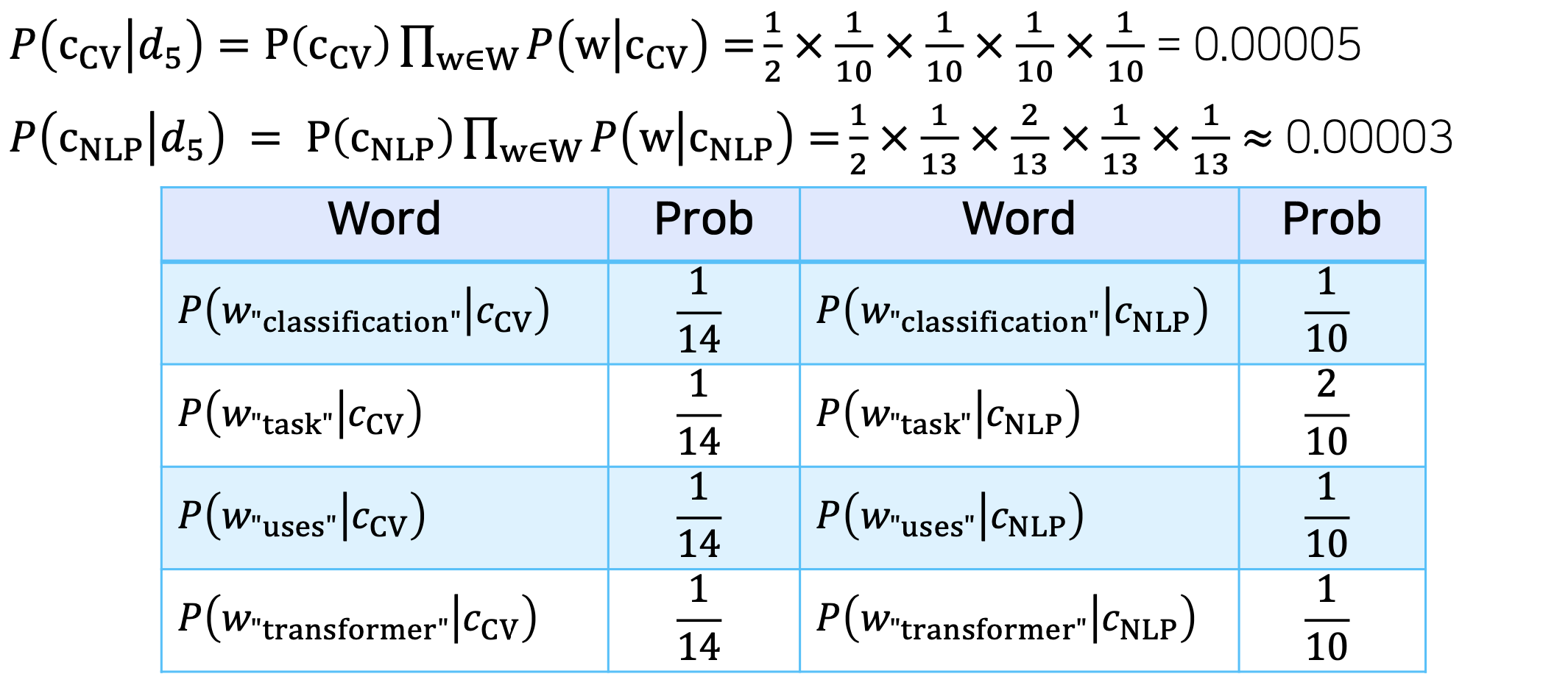
출처: Naver BoostCamp AI Tech - edwith 강의
N-Gram기법을 이용하여 Bag of Words의 단어의 순서를 고려 못하는 단점을 극복 할 수 있다.
=> https://www.youtube.com/watch?v=4f9XC8HHluE

Word2Vec

Word2Vec이란?
단어를 벡터로써 표현하기 위해 고안되어 나온 모델로써 Bag of Words의 한계점을 극복하여 비슷한 단어는 비슷한 벡터로써 표현이 되도록 고안이 되어졌다.
임베딩(Embedding)이란?
사람이 쓰는 언어를 기계가 이해할 수 있는 숫자형태인 vector로 바꾼 결과 혹은 일련의 과정을 임베딩아라 한다.
기본 컨셉은 어떤 단어가 주어졌을 때 그 단어 주변에 어느정도 유사한 단어가 있는지 고려를 하는 것이다.

출처: Naver BoostCamp AI Tech - edwith 강의

즉, "cat"이란 단어 주변에는"meow"란 단어가 많이 나오게 되고 어느 특정한 단어 "X"가 있다고 가정 하고 주변에 "meow"란 단어가 나오게 된다면 이 두 단어는 비슷한 단어라 생각하고 유사한 벡터로써 표현을 하자는 뜻이다.
Word2Vec은 input 데이터가 들어가 hidden layer로 들어가게 되고 output으로써 주변에 있는 단어가 나오도록 학습이 되는 구조로 되어 있으며 w에 해당하는 벡터가 단어를 표현하는 벡터가 되어진다.
주변 단어를 고려 할 때 window size를 고려하여 판단 해 준다.
예) window size1 => 중심 단어를 기점으로 양 옆의 간어 한개 씩 고려

Skip-gram

중심 단어를 가지고 주변 단어들을 예측하는 방식으로 학습되어 진다.

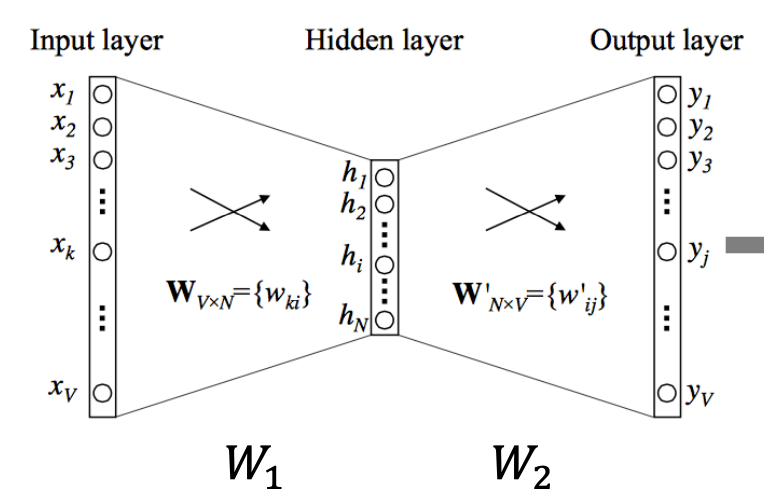
출처: Naver BoostCamp AI Tech - edwith 강의

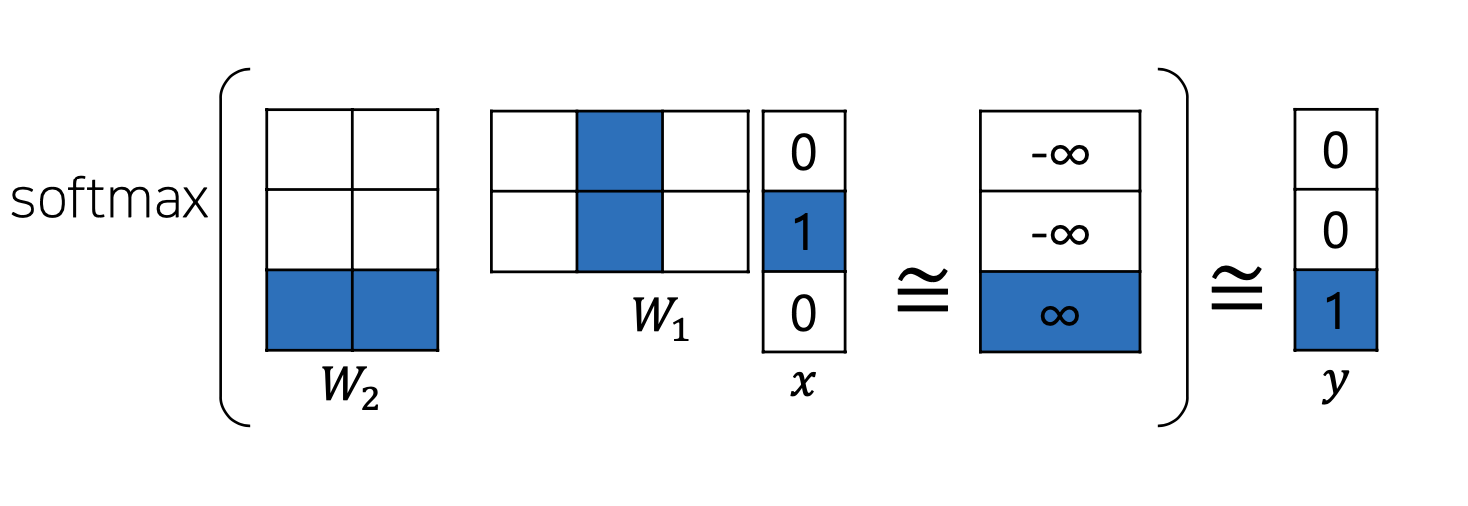
출처: Naver BoostCamp AI Tech - edwith 강의

이때, one hot 벡터의 특징으로 인해 $W_1$ 의 컬럼 벡터중 단어의 인덱스에 해당하는 부분만 추출이 되어 지고 output단어에 해당하는 결과물에 대하여 해당 인덱스 부분만 그 수가 높아져야 하는 방향으로 학습이 되어지기 때문에 $W_1$ 의 column 벡터와 $W_2$ 의 row 벡터는 이 단어를 나타내는 벡터가 된다.( $W_1$ 의 column 벡터와 $W_2$ 의 row 벡터는 곱했을 때 큰 수가 나와야 함으로 양수, 음수의 위치와 비율이 비슷한 벡터가 된다.)
또한,임베딩 벡터를 $W_1$ , $W_2$ 어느것을 사용해도 상관이 없다.(통상적으로는 $W_1$ 를 word Embedding vector로 사용)
참고 사이트 : https://ronxin.github.io/wevi/

CBOW(Continuous Bag-of-Words)

Skip-gram과는 다르게 주변 단어들을 가지고 중심 단어를 예측하는 방식으로 학습
논문상으로 Skip-gram보다 성능이 떨어진다고 표현이 되어 있는데 그 이유를 생각 해 보았을 때 Hidden layer를 생성 할 때, window size * 2 만큼의 단어가 합해져서 은닉층이 생성하게 되는데 이때, Skip-gram에 비해 여러 input데이터에 대하여 합쳐서 고려하여 데이터의 의미가 좀더 섞이게 되고 Skip-gram보단 보다 단순한 Task이기 때문에 성능이 떨어졌지 않았을까 개인적으로 생각을 해 보게 되었다.

출처: Naver BoostCamp AI Tech - edwith 강의

GloVe

GloVe이란?
Word2Vec 임베딩 기법은 확률적 요소를 사용하지 않아 다소 성능이 떨어진다고 생각하여 더욱 성능을 높이고자 고안된 모델이다.
동시등장확률(the words’ probability of co-occurrence)이란?
동시 등장 확률은 특정 단어의 전체 등장 횟수를 카운트하고, 특정 단어가 등장했을 때 다른 특정 단어 k가 등장한 횟수를 카운트하여 계산한 조건부 확률이다.

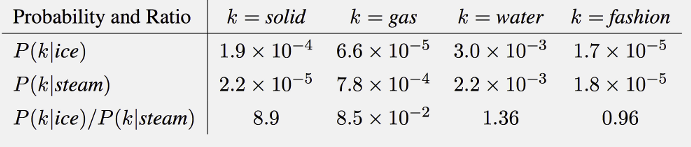
출처: Naver BoostCamp AI Tech - edwith 강의

$P(solid|ice)$ 의 의미는 ice라는 단어가 주어졌을 시 solid라는 단어가 등장할 확률이다.
이와 마찬가지로 $P(k|ice)/P(k|steam)$ 의 의미는 ice라는 단어가 주어졌을 시 k라는 단어가 등장할 확률을 steam이라는 단어가 주어졌을 시 k라는 단어가 등장할 확률로 나눠준 것이다.

출처
https://nlp.stanford.edu/projects/glove/
GloVe모델은 특정 단어 k가 주어졌을 때 임베딩된 두 단어의 내적이 두 단어의 동시등장확률 간 비율이 되게끔 만드는 것을 목표로 모델링 하였다.
$F(w_i,w_j,\tilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$
논문에서는 위와 같은 식을 정의 한 후 만족하는 F함수를 찾는 과정으로 진행을 하였다.
이때, $P_{ik}$ 는 $P(i|k)$ 를 뜻한다.
이때, 논문에서는 위의 식을 아래와 같이 변형 하였는데 $w_i,w_j,\tilde{w_{k}}$ 의 관계를 따져보기 위하여 $w_i,w_j$ 를 뺀 벡터에 $\tilde{w_{k}}$ 를 내적하였다.
또한, 임베딩된 두 단어의 내적이 두 단어의 동시등장확률 간 비율이 되게끔 만드는 것을 목표로 모델링을 하여야 하기 때문에 $P_{ik}를 F(W_i^tW_k)$ 로 정의하였다.
이에 따라 F함수는 아래와 같은 식을 만족을 해야 한다.
1, $F(w_i-w_j,\tilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$ $\\$
2, $F((w_i-w_j)^T\tilde{w_{k}}) = \frac{P_{ik}}{P_{jk}}$ $\\$
3, $F((w_i-w_j)^T\tilde{w_{k}}) = \frac{F(W_i^tW_k)}{F(W_j^tW_k)}$ $\\$
4, $F(w_i^T\tilde{w_{k}}-w_j\tilde{w_{k}}) = \frac{F(W_i^tW_k)}{F(W_j^tW_k)}$
이때, F는 아래의 3가지 조건을 충족하여야 한다.
1, $w_i \leftrightarrow \tilde{w_k}$
: 중심단어는 얼마든지 바뀔 수 있다.(둘 사이의 관계가 중요하기 때문에 값이 동일해야 한다.) $\\$
2, $X \leftrightarrow X^T$
: $X$ 는 co-occurrence matrix를 뜻하는데 2차원 배열에 각 단어마다 window size안에서 얼마나 주변에 있는지 갯수를 Matrix안에 저장 해 놓은 형태로써 transepose해도 형태는 동일해야 한다.
(https://www.youtube.com/watch?v=uZ2GtEe-50E&t=1540s - 12:23) $\\$
3, $F(X-Y) = \frac{F(X)}{F(Y)}$
: 정의역의 뺄셈이 나눗셈의 형태로써 표현 될 수 있어야 한다.(위에 있는 F가 식을 만들어야 하는 조건 참조)
이러한 형태는 지수 함수가 만족을 시킬 수 있고 목적 함수를 만들어 내는 과정은 다음과 같다.
1, $exp(w_i^T\tilde{w_{k}}-w_j\tilde{w_{k}}) = \frac{F(W_i^tW_k)}{F(W_j^tW_k)}$ $\\$
2, $W_i^tW_k = logP_{ik} = logX_{ik}-logX_{i}$
(위에서 $\frac{P_{ik}}{P_{jk}} = \frac{F(W_i^tW_k)}{F(W_j^tW_k)}$ 를 만족해야 한다고 했음으로) $\\$
3, $w_i \leftrightarrow \tilde{w_k}$ 를 만족해야 하는데 $logX_{i}$ 이 항으로 인하여 자유롭지 못하다.
따라서, 이 부분을 상수 형식으로 치환을 해 주는 형식을 취해준다.
$W_i^tW_k = logP_{ik} = logX_{ik} -b_i - \tilde{b_k}$
i,k가 바뀌어도 영향이 가지 않는다.
이때, $X \leftrightarrow X^T$ 가 만독하도록 설계가 되어 있어 $logX_{ik}$ 부분도 상관이 없다. $\\$
4, $W_i^tW_k + b_i + \tilde{b_k} = logX_{ik}$ $\\$
5, $J = \sum_{i,j=1}^V(W_i^tW_k + b_i + \tilde{b_k} - logX_{ik})^2$
위와 같은 목적 식을 완성 할 수 있게 된다.(gradient descent)
이때, 구해야 하는 하이퍼 파라미터는 $w_i,w_j,b_i, b_j$ 이다.
마지막으로 하나의 작업을 더 취하게 되는데 어느 특정 단어의 수가 많은 경우(이때, noise가 끼었다고 표현을 한다.)학습이 잘 안 이뤄질 수 있게 되는데 이러한 상황을 방지 하기 위해 다음과 같은 조취를 취하게 된다. $\\$
$J = \sum_{i,j=1}^Vf(X_{ij})(W_i^tW_k + b_i + \tilde{b_k} - logX_{ik})^2$
where $f(x) = \left\{\begin{matrix} (\frac{x}{x_{max}})^\alpha \\ 1 \;otherwise \end{matrix}\right.$ $if\; x < x_{max}$

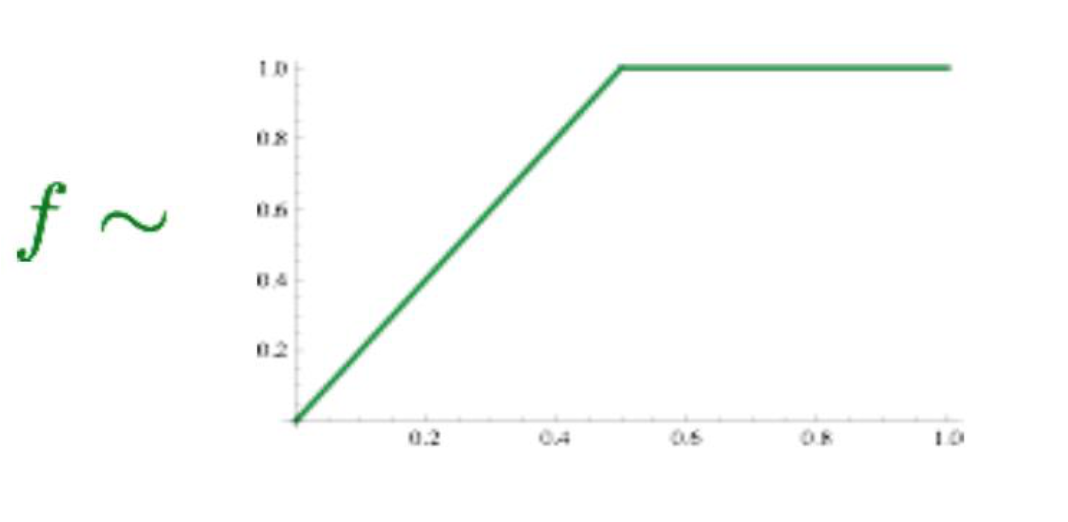
출처: Naver BoostCamp AI Tech - edwith 강의

즉, 함수 f로써 값을 조절하는 장치를 적용한다.
실제로 GloVe도 우수한 성능을 보임을 알 수 있다.

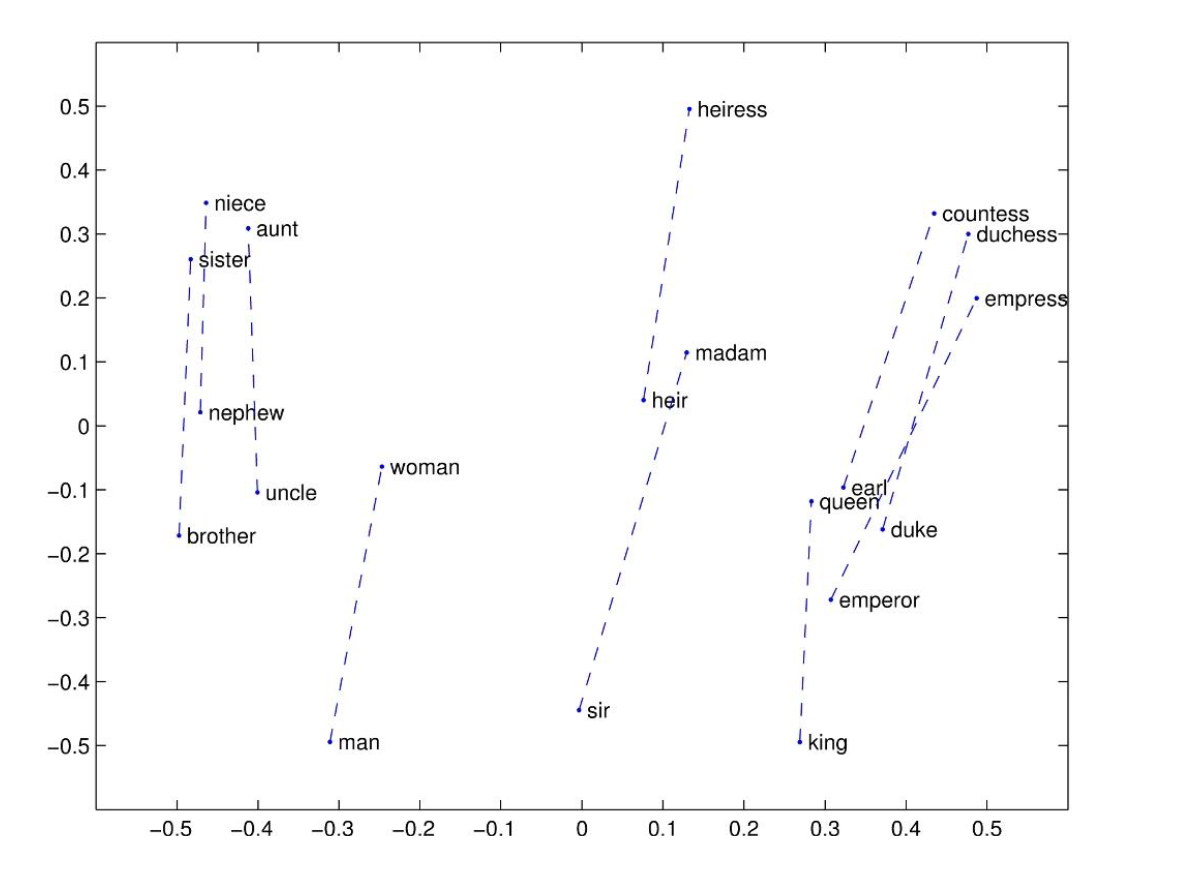
출처: Naver BoostCamp AI Tech - edwith 강의

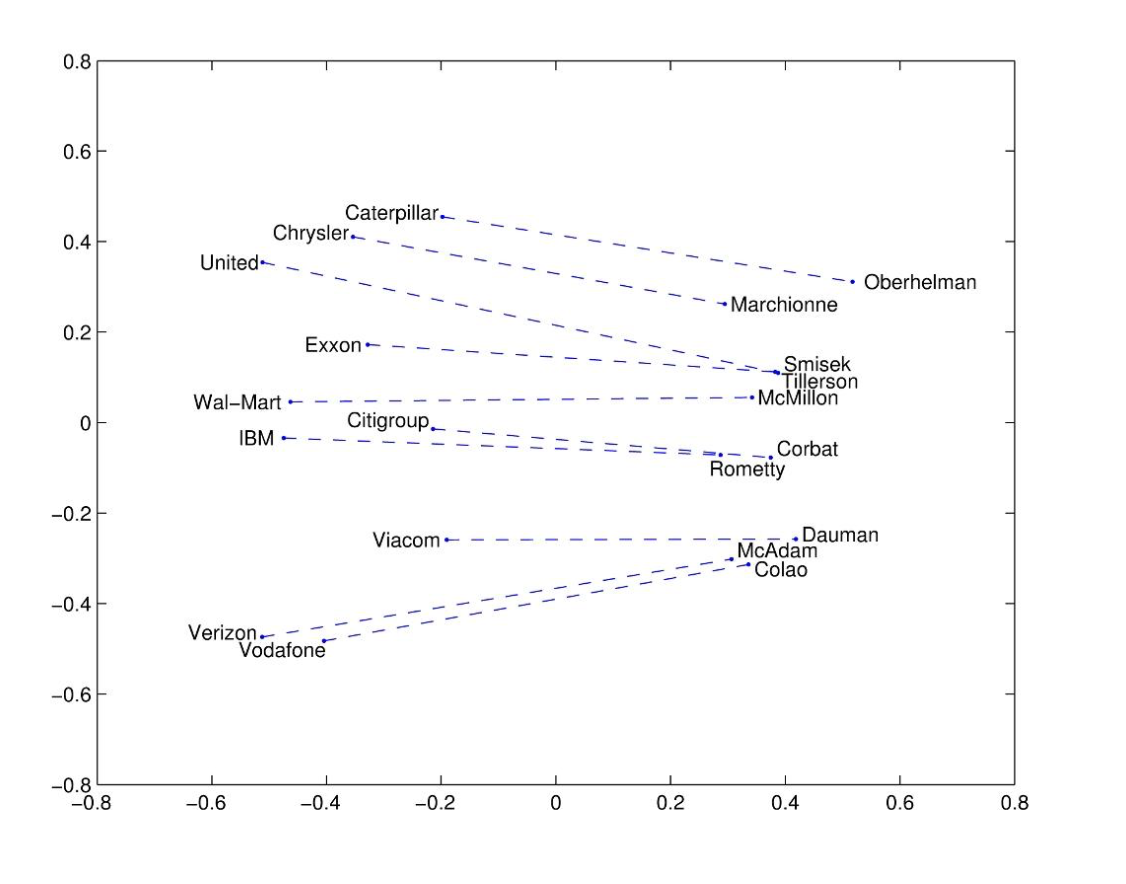
출처: Naver BoostCamp AI Tech - edwith 강의