Transformer

Transformer

---

• Transformer란?
  기존의 RNN방식에서 탈피하여 기존에는 Seq2Seq의 모델에 Attention을 사용하는 구조였으나 Attention만 사용하는 기법으로 만들어진 모델이다.
  
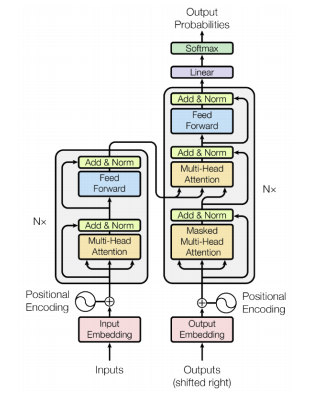
  출처: Naver BoostCamp AI Tech - edwith 강의

• 기존의 RNN의 방식은 길이가 긴 sequence에 대하여 약점이 있었으나 Transformer는 Multi - Head Attention으로 이를 극복하였다.

Encoder

---

• Encoder부분은 Multi - Head Attention 방식으로 진행이 된다.
  
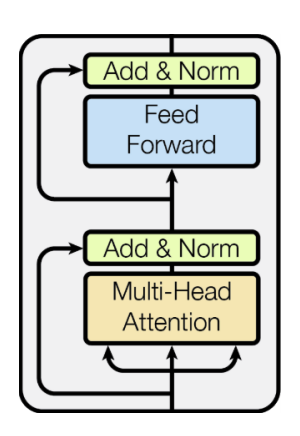
  출처: Naver BoostCamp AI Tech - edwith 강의

• Head의 구조와 연산의 진행 방법은 다음과 같다.
  
  
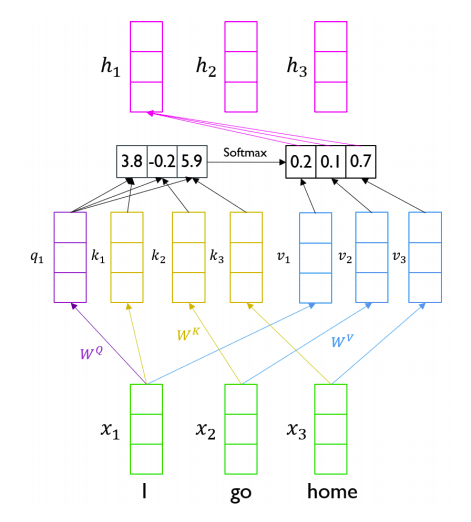
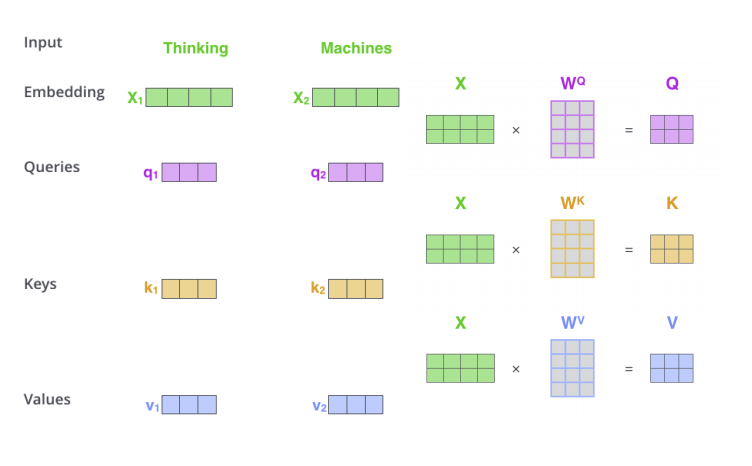
  출처: Naver BoostCamp AI Tech - edwith 강의
  각각의 input에 대하여 encoder hidden state vector(encoder vector)를 구하게 된다.
  이 encoder hidden state vector를 구하는 방법은 다음과 같다.
  1, Q : Query vector라고 하며 각각의 input에 대한 선형 변환으로써 구하게 된다.
  
  2, K : Key vector라고 하며 각각의 input에 대한 선형 변환으로 이뤄지게 되고 향후 Query vector와 연산을 진행하며 이 연산과정으로 나온 Scalar값은 기존 Query vector와 Key vector를 산출한 input에 대한 Attention의 정도를 나타내게 된다. (이에 따라, Query vector의 column수와 Key vector column은 향후 transpose연산을 한 후 내적 연산이 수행되야 하기 때문에 같아야 한다.)
  
  3, V : Value vector라고 하며 각각의 input에 대한 선형 변환으로 이뤄지게 되고 Q, K에서의 연산 과정을 통해 나온 값으로 가중 평균을 구하여 최종 encoder hidden state vector를 구하게 된다.(이때, K, V벡터의 갯수는 동일해야 한다.)
  
  4, demension의 특징을 정리해 보게 되면 q,k 의 demension은 $d_k$로 같아야 하지만 v의 demension은 $d_v$로써 같지 않아도 된다.
  
  핵심 point는 각각의 K, V벡터는 어느 Q 벡터에 대해서도 동일한 벡터로 연산이 되어지고 이에 따라 멀리있는 데이터도 유실이 되지 않는다는 장점을 가질 수 있다.

• 수식 표현
  $A(Q,K,V) = \sum_i\frac{exp(Q \cdot K_i)}{\sum_jexp(Q \cdot K)}$ -> $A(Q,K,V) = softmax(QK^T)V$
  
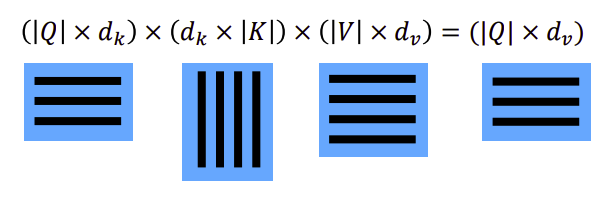
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  위와 같이 여러개의 input을 하나의 행렬로써 처리가 되어 진다.
  또한, 실제 Transformer 구현을 할 때에는 보통 동일한 shape로 mapping된 q, k, v가 사용된다.

• scaling
  Dot product연산에는 한가지 문제점이 있다.
  
  
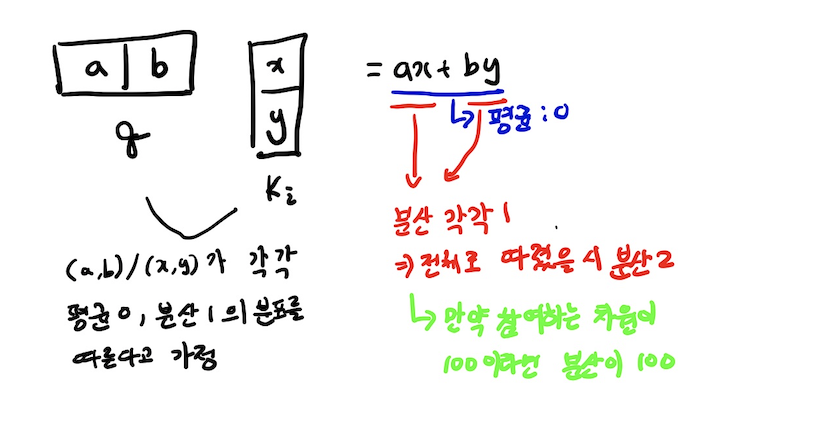
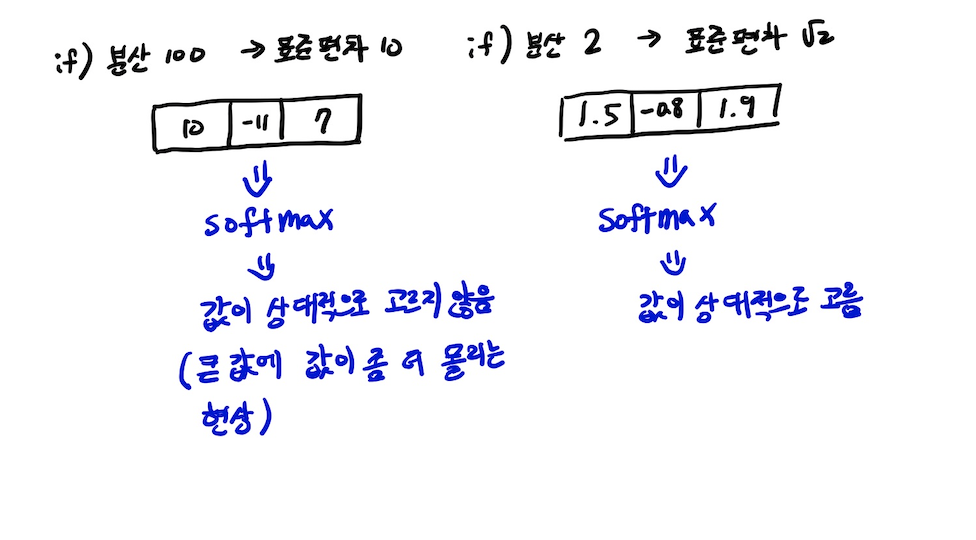
  즉, 분산이 점점 커지게 되어 값이 고르지 않는 현상이 나타나게 되는데(이로 인해 demension $d_k$가 매우 커지게 되면 값 쏠림 현상이 일어나고 이로 인해 gradient vanishing 현상이 일어나게 된다.) 이를 방지하기 위해 scaling을 해 주게 된다.
  
  방법은 q, k의 내적 연산의 결과의 각각의 원소에 $\sqrt{d_k}$를 나눠주게 된다.
  $A(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$

• Multi - Head Attention
  위의 방법은 하나의 Head에 대한 가중치 벡터의 학습 과정이고 이를, 여러번 수행하는 개념으로써 여러 버전의 W만큼 hidden state vector가 나오고 이를 모두 concat하여 hidden state vector를 구하게 된다.
  
  왜 이러한 방법을 사용하게 되는 것일까?
  다양한 관점에서 Attention값을 보고자 사용을 한다.
  즉, 예를 들어 어느 관점에서는 품서 측면에서 고려하자는 것이고 어느 관점에서는 의미론적으로 고려하고 이런 식으로 다양한 관점에서 보고자 이 방법을 사용하게 된다.
  
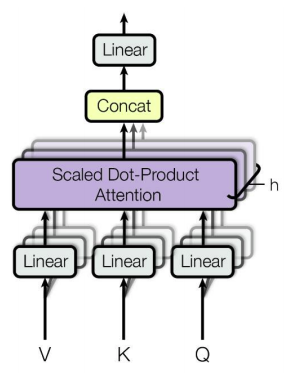
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  $MultiHead(Q,K,V) = Concat(head_1 , ... , head_h)W^O$
  where $head_i = Attention(QW_i^Q, KW_i^K,VW_i^V)$
  실제 코드 구현 상으로는 여러개의 Q를 구하는 것이 아니라 하나의 큰 Q를 구한 다음 잘라서 코드 구현을 하게 해 준다.
  
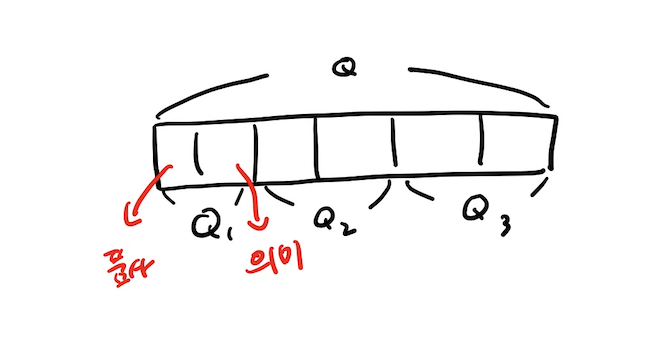
  (k, v도 마찬가지 방법으로 구현을 해 주게 된다.)
  
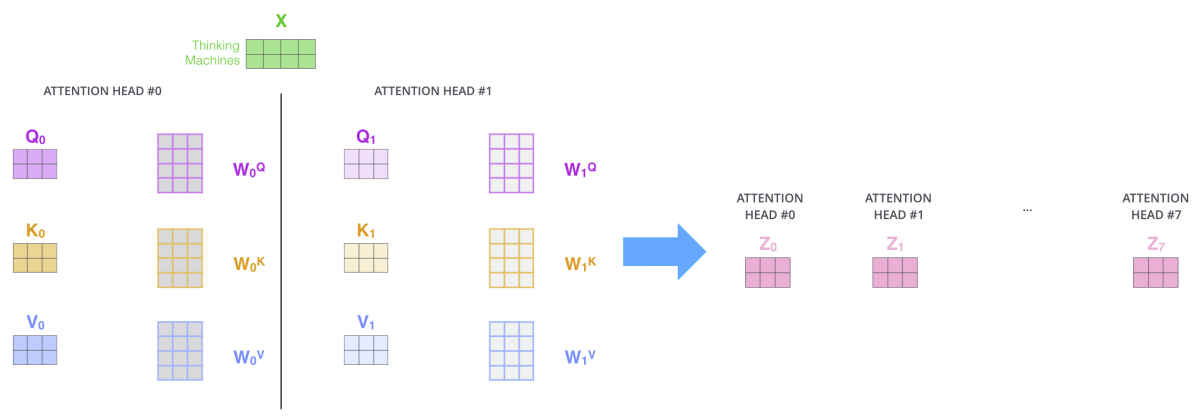
  출처: Naver BoostCamp AI Tech - edwith 강의
  
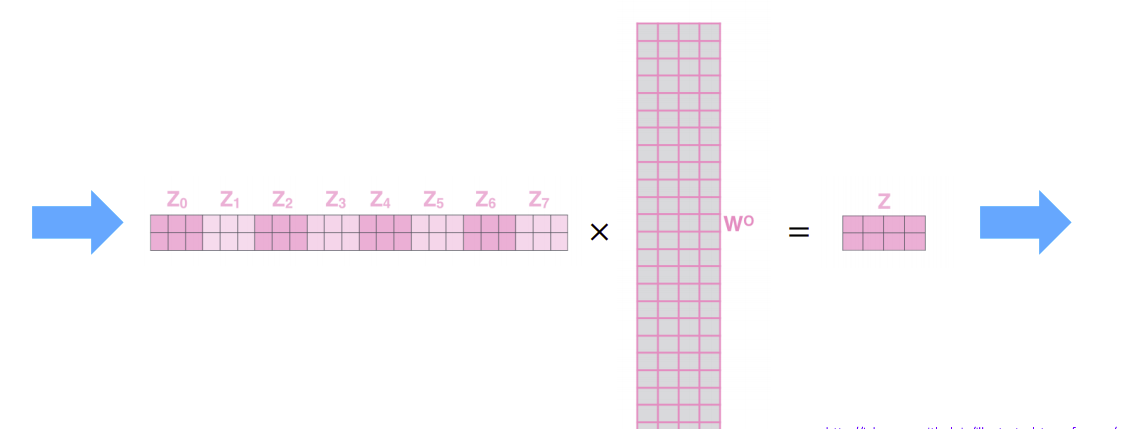
  출처: Naver BoostCamp AI Tech - edwith 강의

• 성능 차이
  
  출처: Naver BoostCamp AI Tech - edwith 강의/ Attention Is All You Need, NeurIPS’17
  
  위의 지표에서 self-Attention과 Recurrent(RNN)부분을 보게 되면 n은 sequence length, d는 dimension of representation인데 d는 충분히 조절이 가능하나 n은 쉽게 조절 할 수 없는 값이다.
  
  Complexity per layersms 필요 메모리 양이고 Sequential Operations는 시간 복잡도를 나타내는 것인데 필요 메모리 양 부분을 보게 되면 d는 직접 조절이 가능한 수치를 감안하면 Self-Attentiondl Recurrent(RNN)보다 많은 메모리 부분을 차지하게 된다.
  
  그러나, 시간 복잡도 관점에서 RNN은 이전의 값을 가져와 사용해야 하기 때문에 병렬적 수행이 불가한 반면 Self-Attention은 충분한 GPU가 있다고 가정 하였을 시 병렬적으로 수행이 가능하여 더 빠른 것을 확인 할 수 있다.
  
  마지막 부분인 Maximum Path Length은 과거 단어의 정보를 담기 위한 길이인데 이도 마찬가지로 이전의 값을 지속적으로 가져야 하는 RNN의 특성으로 인해, 어느 위치든 상관없이 정보를 가져올 수 있는 Self-Attention의 특성으로 인해 위와 같은 결과를 볼 수가 있게 된다.
  
  정리해보면 RNN과 Self-Attention의 특성으로 인해 학습은 Self-Attention이 빠르나 메모리와 필요한 연산장치가 많이 필요로 하게 되는 것을 알 수 있다. 또한, Self-Attention은 장점은 필요한 위치의 정보를 일련의 과정을 거치지 않더라도 바로바로 가져 올 수 있다.
  (참고로, k : kernel size of convolutions, r : size of the neighborhood in restricted self-attention를 각각 뜻하게 된다.)

• 추가적인 후처리
  Multi - Head Attention을 수행하고 ADD 와 Norm연산을 수행하게 되는데 ADD는 residual connection이라 하고(vision쪽에서도 많이 사용되는 기법으로 gradient vanishing문제를 해결하기 위한 수단) Norm은 residual normalization 이라한다.
  

  • residual connection은 다음 예시와 같이 수행이 된다.
    
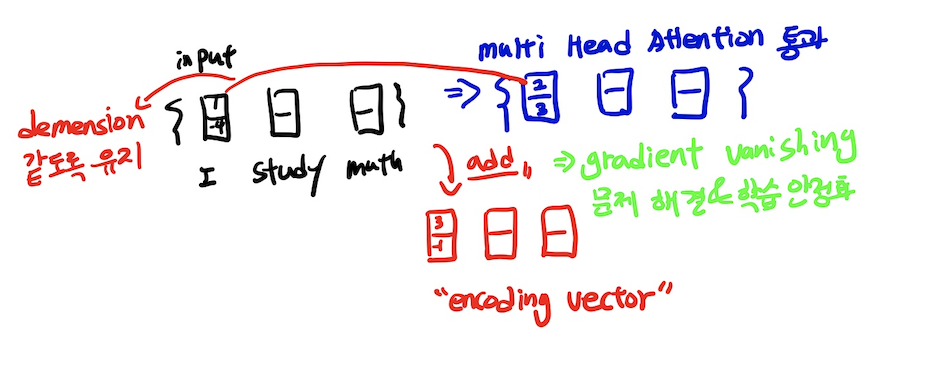
    즉, Multi - Head Attention연산을 통과 한 후 input값을 더해주는 형식이다.
  • residual Normalization
    
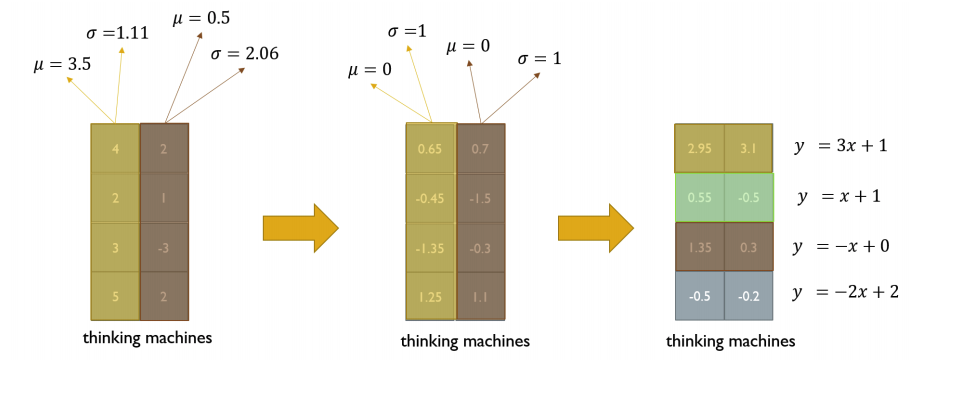
    주어진 값들에 대한 정규화를 하는 과정으로써 평균은 0, 분산을 1로 만들어 준 후 원하는 평균과 분산을 주입 할 수 있는 선형변환으로 이뤄져 있다.
    
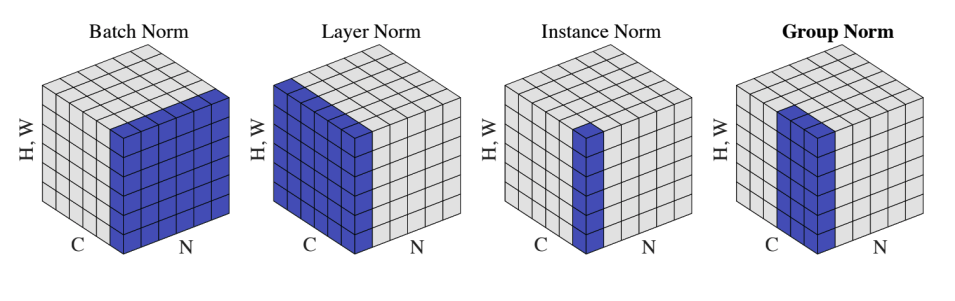
    위와 같이 다양한 종류의 Norm이 존재하게 되며 1)각각의 Batch데이터들을 통합하는 기준으로 정규화를 수행을 해 주는 Batch Norm 2)하나의 Batch안 특징들을 정규화 해 주는 Layer Norm등 다양한 Norm들이 존재한다.
    
    정규화를 해 주는 방법을 Batch Norm을 기준으로 예를 들면 다음과 같다.
    
    layer Norm을 기준으로 예를 들면 다음과 같다.
    
    출처: Naver BoostCamp AI Tech - edwith 강의
    

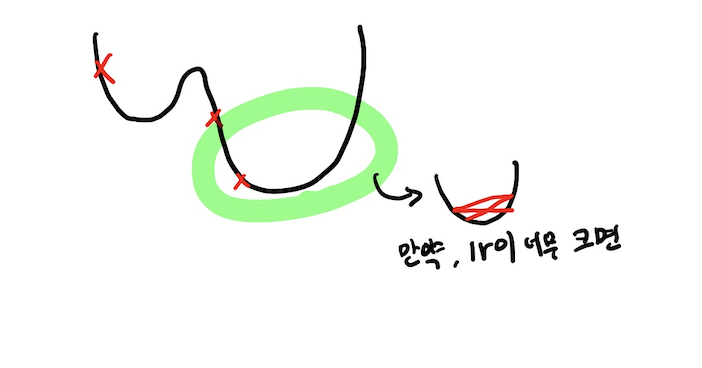
• Transformer의 약점이 있다면 순서가 고려가 안되면서 encoding vector가 생성된다는 점이다.
  예를 들어, I go home 과 home go I가 input으로 들어가게 되면 I에 대한 encoding vector는 같다.
  (이 이유에 관해서는 개인적으로 생각을 해 보았을 때, 역전파가 수행 될 시 Attention Output을 통해 수행을 하게 되며 순서를 고려하지 않은 채로 한번에 역전파가 전달되면서 위와 같은 현상이 이뤄지는 것 같다.
  정리 부분 - https://velog.io/@ganta/Language-Modeling-Seq2Seq-Attention)
  
  이러한 부분에 있어서 RNN과는 차이점이 생기고 다소 약점이 생길 수 있는 부분이 되는데 Transformer에서는 Positional Encoding으로써 위와 같은 문제를 해결하고자 하였다.
  $PE_{(pos,2i)} = sin(pos/10000^{2i/d_{model}})$
  $PE_{(pos,2i+1)} = cos(pos/10000^{2i/d_{model}})$
  위와 같은 주기함수를 사용하였고 이를 그래프와 그림으로써는 아래와 같이 표현이 가능하다.
  
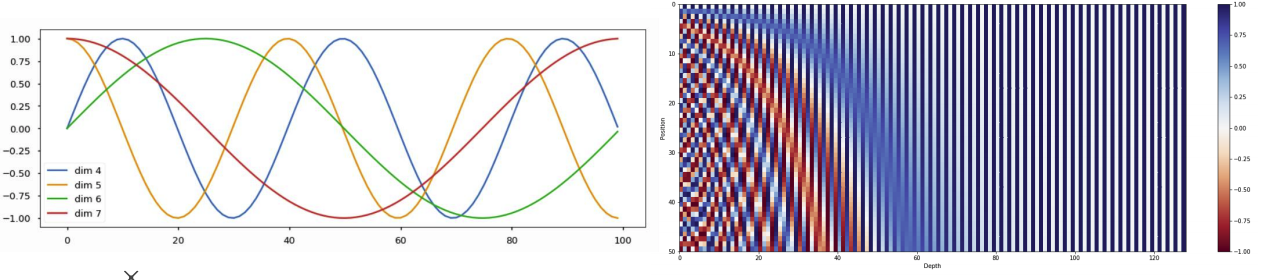
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  왼쪽 그래프는 각각의 dimension마다의 주기 함수를 그린 것으로 x축은 각각의 input으로 들어온 순서(인덱스)마다 각각의 dimension마다 더해줄 값이 y축의 값이 된다.
  오른쪽의 그림은 x축은 dimension을 뜻하며 y는 input으로 들어온 순서(인덱스)를 나타내고 색은 더해준 값을 나타내게 된다.

• Transformer 에서는 learning rate또한 유동적으로 조절을 해 주게 되는데 이를 learning rate scheduler라고 한다.
  
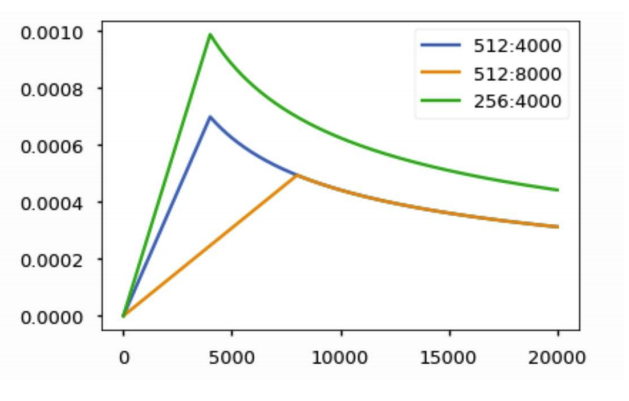
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  위의 그래프의 x축은 epoch을 나타내고 y축은 learning rate(lr)를 뜻하는데 학습 초기에는 그래프가 가파르기 때문에 lr을 작게 해 주고 최저점 근처로 갈수록 lr의 값을 키워주며 완전 근처에서는 이리저리 튈 수 있기 때문에 다시 lr을 줄여주는 모습을 보여주게 된다.
  

Decoder

---

• Encoder부분과 굉장히 비슷하나 한가지 차이점은 Masked Multi-Head Attention이다.
  
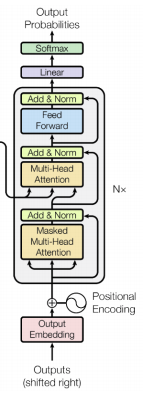
  출처: Naver BoostCamp AI Tech - edwith 강의
  
• Masked Multi-Head Attention은 encoder부분과는 다르게 test수행 시 이전값이 그 이후의 값을 미리 알 수 없기 때문에 서로 간의 관계를 도출 할 때 제외를 시켜 주워야 한다는 개념에서 나오게 되었다.(train때는 teacher forcing방법으로써 ground tool을 넣어주워 input값을 알 수 있으나 실제 수행시에는 이후의 현재 time step이후의 input값을 모른다.)
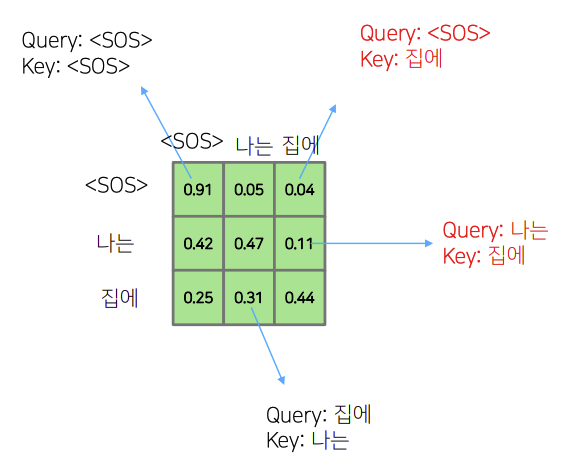
• 실제 예시를 들어보게 되면 다음과 같다.
  
  
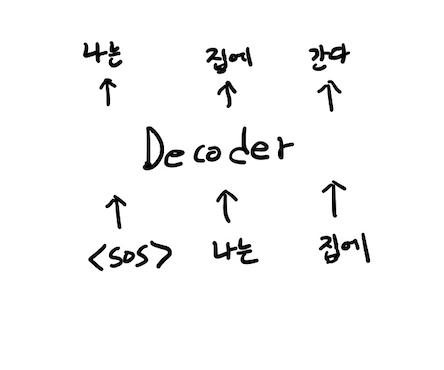
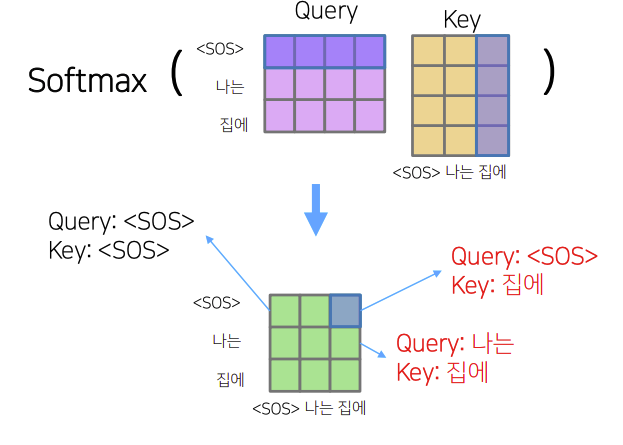
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  
  출처: Naver BoostCamp AI Tech - edwith 강의
  
  
  출처: Naver BoostCamp AI Tech - edwith 강의
  
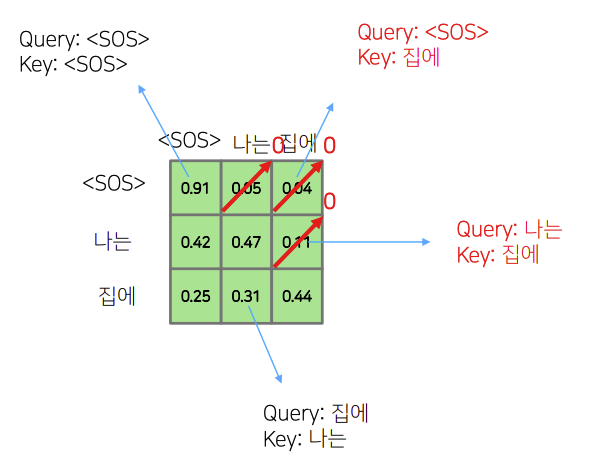
  이때, "나는"이라는 input을 생각 해 보았을 때 다음 input인 "집에"라는
  값을 time step시점에서 알지 못함으로 이 관계를 0으로 만들어 준 다음 row의 합이 1이 되도록 비율만큼 값을 조절하여 값을 설정하여 준다.(실제 코드 구현에서는 0부분으로 만들어 주는 부분을 -$\infty$으로 만들고 softmax를 통과시켜 주워 확률을 산출한다.)

기타

• 왜 sequential modeling은 어려운 문제일까?
  입력값이 정직하게 들어올 경우가 있지만 끝 부분, 혹은 중간의 일부분이 생략되어 있는 경우 등 여러 다양한 input에 대하여 유연하게 대처해야 하기 때문이다. => transformer는 이러한 문제를 해결해 주게 되었다.
• 입력값에 대한 보다 유연한 처리를 위해 최근에는 Transformer모델을 많이 사용하고 있고 기게어, 이미지 분류, 이미지 detection, 심지어 문장에 맞는 이미지를 띄우는 DALL-E까지 다양한 분야에서 좋은 성능을 보이고 있다.
• Transformer에 대하여 정리가 잘 되어있는 블로그가 있어 함께 올려 놓겠습니다.
  영어 버전 -> http://jalammar.github.io/illustrated-transformer/
  한국어 버전-> https://nlpinkorean.github.io/illustrated-transformer/

Reference

Naver BoostCamp AI Tech - edwith
http://jalammar.github.io/illustrated-transformer/
https://nlpinkorean.github.io/illustrated-transformer/