ch 6-3. 합이 K 되는 숫자

📌 동적계획 -> 백트래킹 알고리즘 이유

앞에서 동적 계획 알고리즘으로 해결했음
but 수행시간이 O(nK)인데,
K = 2^n 지수형태 처럼 매우 크면 수행시간 엄청 오래걸림
이제 백트래킹 알고리즘을 이용하자

• 가지치기로 해가 될 수 없는 노드들을 탐색 안 함
  -> 모든 조합을 검사하는 것보다 훨씬 빠름

📌 백트래킹 알고리즘

1. 주어진 숫자들을 증가 순으로 정렬
2. 순서대로 숫자 선택하는 경우(o) & 포기하는 경우(x)로 나눠 상태 공간 트리의 노드 만듦

• 만약 노드 만들 수 없거나 만들 필요 없으면,
  부모 노드로 되돌아가서 다른 노드 선택
• 부모 노드로 되돌아가는 것 = '가지치기'

3. 위에서 선택한 노드에서 해를 찾으면 알고리즘 종료
   해가 아니면 [2] 다시 수행

📌 가지치기(prunning)

• 입력을 정렬하는 이유 : 자식 노드를 만들 때 다음 숫자 추가한 합이 K 초과하면
  그 이후의 숫자는 이미 다음 숫자보다 크므로 만들어진 노드 아래로 탐색해도 해 없음

• 탐색 중단 = "가지치기"

• 탐색 중 남은 숫자들을 다 더해도 K보다 작은 경우에도 가지치기함

📌 상태 공간 트리

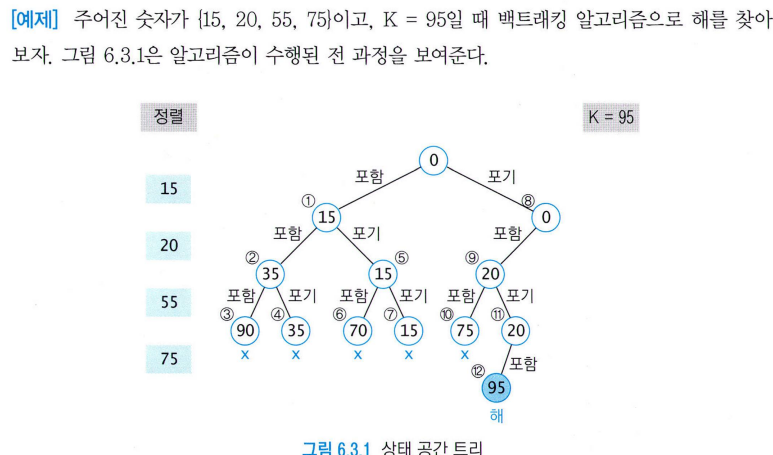
• 노드 속 숫자 : 루트에서 그 노드까지 포함시킨 숫자들의 합
• 두 자식을 가진 각 노드에서
  - 왼쪽 자식 : 포함
  • 오른쪽 자식 : 포기

계산 순서 참고!

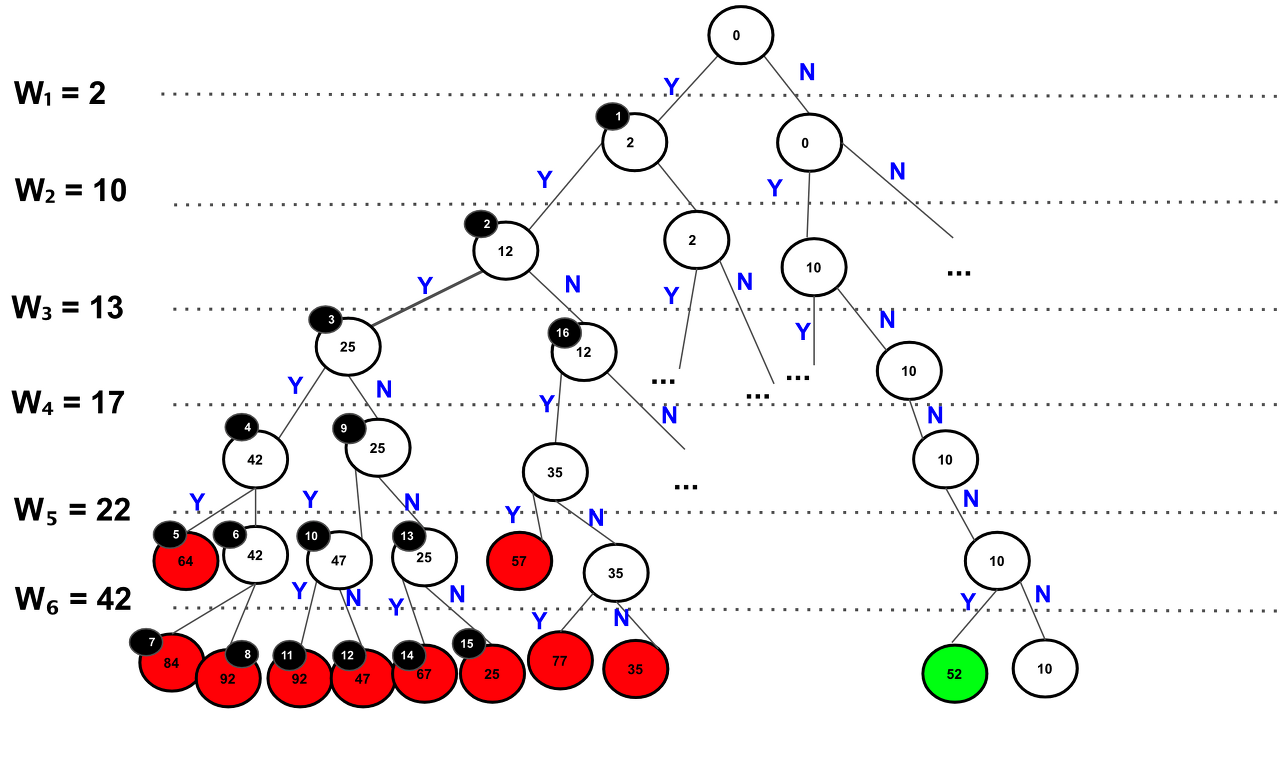
📌 수행시간

상태 공간 트리에서

• 1개 노드 -> 2개의 자식노드 가짐
• 트리 높이 : n+1
  ➡️ 트리의 총 노드 수 : 2^(n+1) - 1

각 노드에선 수행하는 계산

1. 현재 선택된 숫자의 합과 K를 비교
2. 숫자 포함하면 기존의 합에 숫자 더하고,
   leftover(남은 수들의 총합)에서 현재 선택한 숫자 빼는 뺄셈함
   ➡️ O(1)시간 걸림

총 수행시간

트리의 총 노드 수 * 각 노드에서의 수행시간 = {2^(n+1) - 1} x O(1) = O(2^(n))