ch 6-4. 배낭 문제

📌 분기 한정 알고리즘 이용한 배낭 문제

• 앞에 5.5장에서 배낭 문제를 동적 계획 알고리즘으로 해결했음
  => 배낭 DP알고리즘의 수행 시간 : O(nK)

if K = 2^n이라면 DP 알고리즘은 모든 조합을 하나씩 차례로 검사해보는 방법보다도 성능 떨어짐

배낭 문제 : n개의 물건의 무게 & 가치 주어짐
배낭의 용량이 K일 때 최대 가치를 얻기 위해 담아야 할 물건들 찾는 문제

💡 분기 한정 알고리즘 쓰려면

상태 공간 트리 탐색하면서 새 노드를 만들 때 그 노드의 한정 값(bound)을 계산해야 함!

• 노드의 한정 값 bound : 그 노드가 얼마나 해에 가까운지 알 수 있는 수치
• 배낭 문제 : 최대 가치를 찾는 문제
  ➡️ 높은 한정 값 가진 노드들을 우선하여 탐색
• 최선 우선(Best-First)탐색 수행

📌 노드의 한정 값 bound

1) bound의 값

• 배낭 용량 초과 안 하면서 최대 가치 얻는게 목적
• bound = 해당 노드로부터 탐색하면 얻을 수 있는 최대 가치(예측값)

2) bound 값 계산 방법

💡 쉽게 생각해서
현재 담긴 가치 + (물건 무게 초과 안 하게 최대로 담을 때 얻는 가치 + 자투리 무게 x 안 담은 물건의 단위무게 당 가치)

bound = [현재 담겨있는 물건의 가치] + [배낭의 남은 부분에 앞으로 담을 물건의 가치]

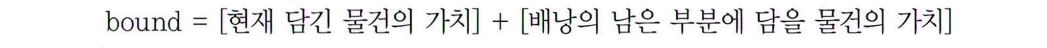
📌 알고리즘

1. 단위 무게 당 가치를 기준으로 물건들을 내림차순 (큰 것부터) 정렬
2. 상태 공간 트리의 루트 만듦
3. 물건을 포함(왼쪽) / 포기한 자식 노드 (오른쪽) 만들고 각각 bound 계산
4. 상태 공간 트리의 이파리 중 가장 큰 bound 가진 노드 선택
   - 남은 이파리 중 더 큰 bound값 없으면 알고리즘 종료
5. go to 3번 후 과정 반복

➡️ 해 : 배낭에 담을 수 있는 가장 큰 가치

🌿 교재 예제

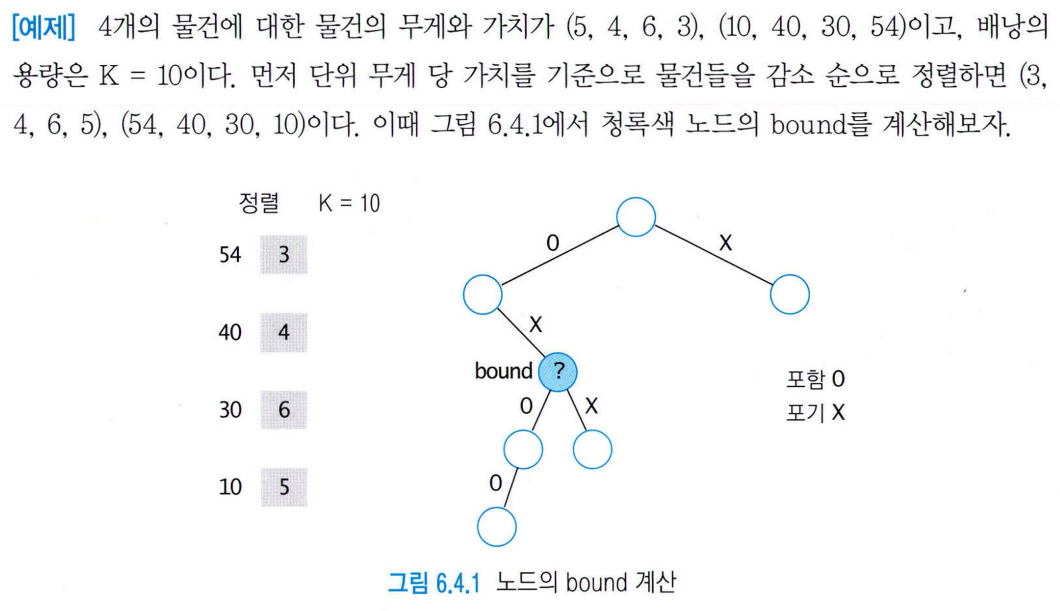
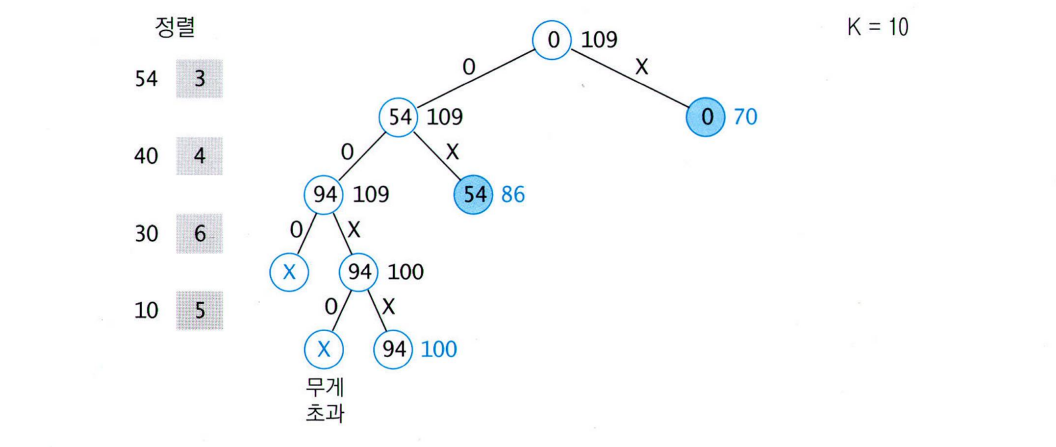
상태 공간 트리에서

• 노드 안의 숫자 = 배낭에 물건 담아서 얻는 가치
• 노드 옆의 숫자 = 그 노드의 bound

각 노드의 bound 계산

1. 루트 노트의 bound
   : 54 + 40 + (10-7)x30/6
2. 2번째 노드의 bound

📌 수행시간

• O(2^n) = 분기 한정 알고리즘의 수행시간 = 백트래킹 알고리즘의 수행시간
• but 분기 한정 알고리즘이 한정 값 이용해 해가 있을만한 곳을 그리디하게 탐색함
  -> 실질적으론 백트래킹보다 빠름