ch 7-1. 외판원 문제(TSP)

NP-완전 문제

지수 시간의 시간 복잡도를 가진 알고리즘으로 해결되는 문제 집합

문제 A가 NP-완전 문제가 되려면

• A가 NP-문제
• 모든 NP-문제가 다항식 시간에 문제 A로 변환돼야 함

NP- 문제는 NP-알고리즘을 가진 문제들의 집합
NP-알고리즘 : '추측된' 해를 다항식 시간에 확인하는 알고리즘

근사 알고리즘

NP-완전 문제 포기

• NP-완전 문제 : 다항식 시간에 해결할 수 있는 알고리즘이 아직 발견 안 됨
• NP-완전 문제를 어떤 방식으로든지 해결하려면 다음의 3가지 중 1가지는 포기해야 함

1. 다항식 시간에 해를 찾는 것
2. 모든 입력에 대해 해를 찾는 것
3. 최적해를 찾는 것

근사 알고리즘

NP-완전 문제를 해결하기 위해 3. 최적해 찾기를 포기하고, 최적해에 근사한(가까운) 해를 찾아주는 알고리즘

근사해를 찾는 대신에 다항식 수행시간 가짐

근사해가 최적해에 얼마나 근사한 것인지(=얼마나 가까운지)를 나타내는 근사 비율을 보여주어야 함

• 근사 비율 = 근사해의 값 & 최적해의 값의 비율
• 1.0에 가까울수록 정확도가 높은 알고리즘
• 근사 비율 계산하려면 최적해 알아야하는 모순이 생김
  ➡️ 대부분 최적해를 대신할 수 있는 간접적인 해 찾아서 근사 비율 계산

7.1 외판원 문제

어느 한 도시에서 출발 - 다른 모든 도시를 1번식만 방문하고, 출발했던 도시로 돌아오는 여행 경로의 거리를 최소화하는 문제

다양한 알고리즘으로 최적해 찾을 순 있으나, 지수 시간 걸림
-> 도시 수가 많아지면 시간이 오래 걸려 최적해 찾기 어려움

➡️ TSP를 위한 근사 알고리즘 ; 최적해는 안 찾고, 다항식 시간에 최적해에 가까운 해를 찾음

TSP와 유사한 문제 : 최소 신장 트리(MST)문제

크리스컬 : 하나의 엣지부터
프림 : 하나의 정점부터 시작

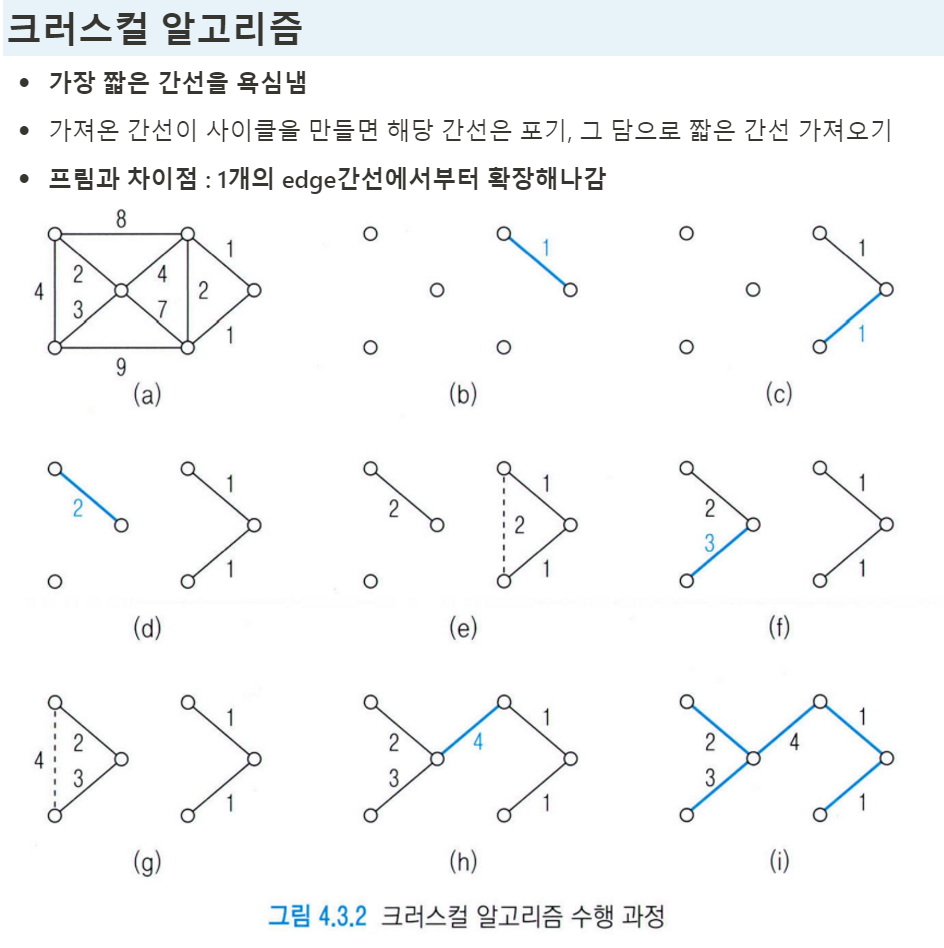
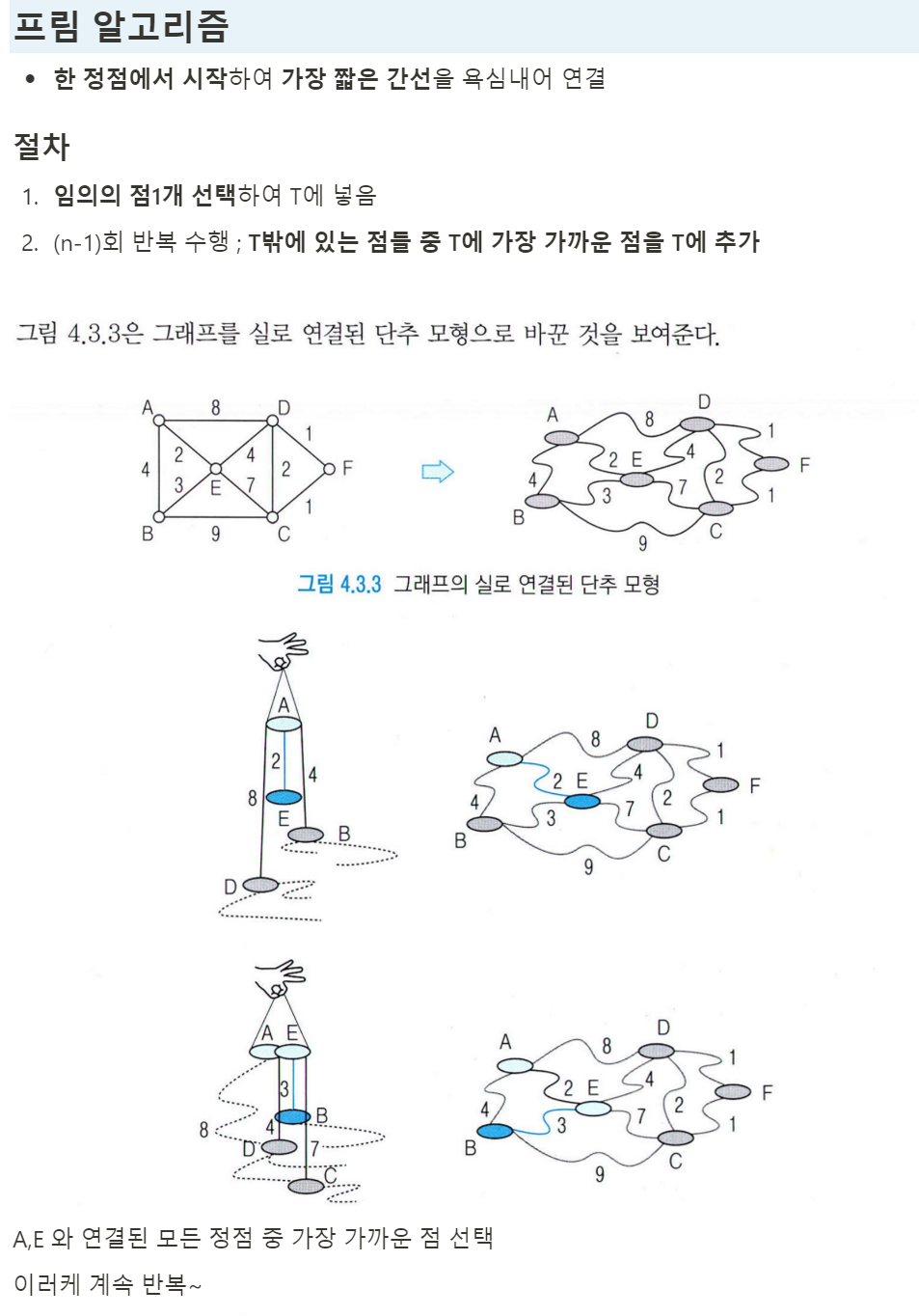
⇒ 총 수행시간 = $O(n^2)$

• MST : 그래프의 모든 점을 사이클 없이 최소의 가중치로 연결

• TSP : 모든 점을 1번씩 최소 비용으로 방문하는 것
  => 유사함!
  

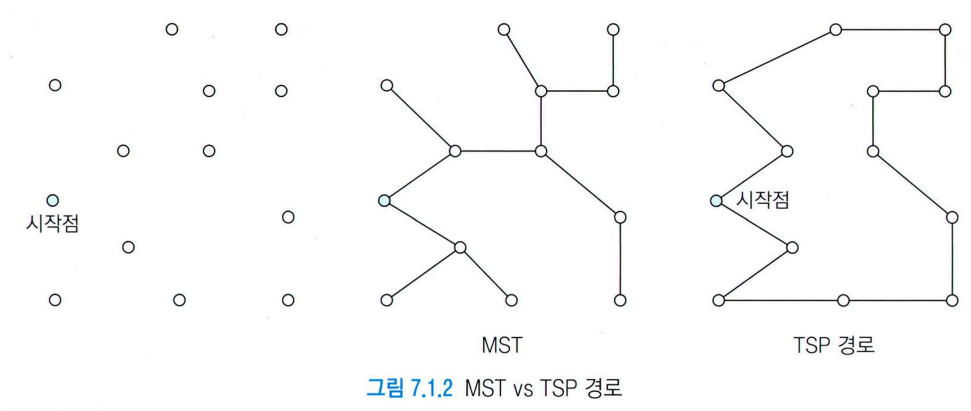
• 차이점 : TSP는 시작점으로 돌아와야 하므로
  TSP 경로의 간선 수 = n
  MST의 간선 수 = n-1 (n개 점 잇기라서)

MST의 간선을 활용하여 어떻게 TSP의 경로를 만들 수 있을까?

1. TSP의 시작점으로부터 MST 만들어서 모든 점을 방문하고 시작점으로 돌아오는 정점 방문 순서 생각해보자.
2. BUT 시작점부터 MST 트리에서 점들 방문하다 보면, 트리에는 사이클 없으므로 1번 이상 방문하는 점들이 생김 (시작점을 제외하고)

예시)

시작점 A라면
A B C D C E C F C B A
=> 시작점 A 제외하고 C,B를 2번 이상 방문함

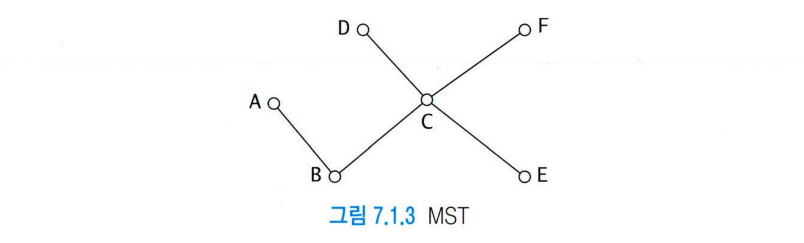
각 점을 1번만 방문하도록 하는 방법 : 지름길

• 트리 방문 순서에서 처음 방문한 경우만 제외하고, 이후에 반복되는 점을 경로에서 제거

아까 경로에서 반복되는 점 첫방문 빼고 지우기
A B C D C E C F C B A
=> A B C D E F A

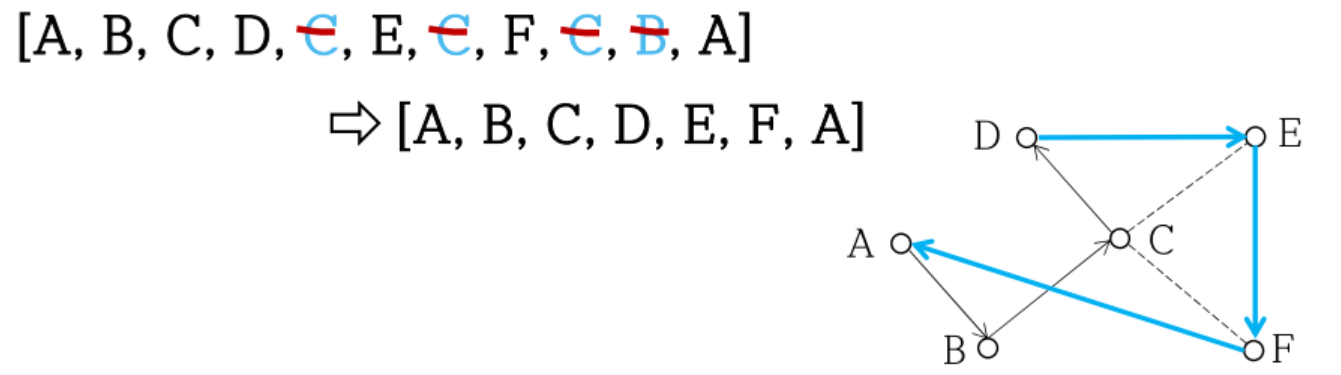
예제) 시작점 = 0

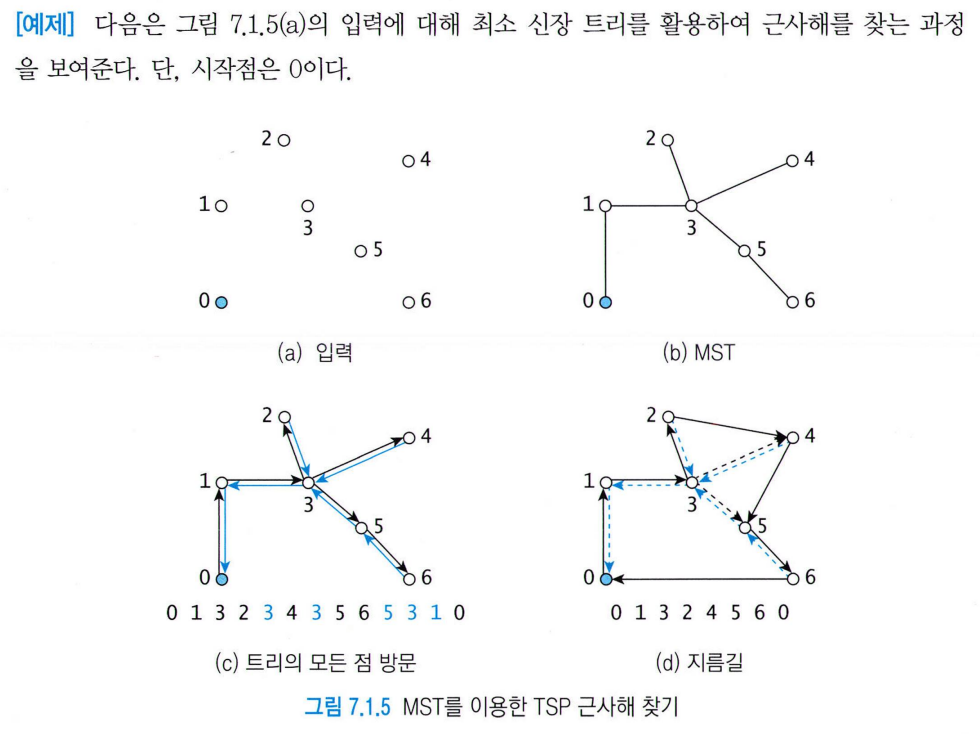
0 1 3 2 3 4 3 5 6 5 3 1 0

• 중복하여 방문하는 도시 제거 과정에 삼각형 부등식 원리가 적용된 것 ; 삼각형 젤 긴 변(= 여기서 지름길임)의 길이는 다른 두 변의 합보다 짧음

TSP 근사 알고리즘

1. 입력 그래프에서 MST인 T 찾음
2. TSP의 시작점으로부터 출발하여 T의 간선을 따라 모든 점 방문하고,
   다시 출발했던 점으로 돌아오는 점들의 방문 순서 찾음
3. 2번에서 찾은 방문 순서에서 중복된 점 제거하여 TSP 경로 만듦
   단, 마지막의 시작점은 제거 안 함

수행시간

1. MST 찾기 : 크리스컬/프림 알고리즘의 수행시간
2. 트리 간선 따라서 점의 방문 순서 얻는 것 ; O(n) 시간 소요 : 트리이므로 간선 수는 n-1개 지남
3. 반복되는 점 제거 : 방문 순서를 왼쪽부터 하나씩 검사하면서 처음 나타나는 점은 놓아두고 반복되는 점 제거 => O(n)

➡️ 수행시간 = MST 찾는 시간 + O(n) + O(n)
=> 크리스컬 / 프림 알고리즘 수행시간과 동일

근사 비율

• 최적해인 MST 간선의 가중치의 합(M)을 최적해의 값으로 간접적으로 활용

TSP 근사 알고리즘이 계산한 근사해의 값은 2M 보단 크지 않음(작거나 같음)

이유

• Step 2에서 MST의 간선을 따라서 방문 순서 찾을 때 사용된 트리 간선을 살펴보면,
  각 간선이 2번씩 사용됨
  => MST로 얻은 이 방문순서에 따른 경로의 총 길이는 2M
• Step 3에선 삼각 부등식 원리 이용 - 샤 방문 순서 만듦
  -> 이전 방문 순서에 따른 경로의 길이보다 지름길 사용한 새로운 경로의 길이가 더 짧음

=> 이전 경로 길이인 2M보다 크지 않음

➡️ 근사 비율 : 2M/M = 2.0보다 크지 않음
즉, 근사해는 최적해의 2배를 넘지 않음