분할 정복 알고리즘(Divide and conquer algorithm)이란?
- 엄청나게 크고 복잡한 문제를 작고 단순한 문제로 조금씩 쪼개어 용이한(풀 수 있는) 문제가 되면 해당 문제를 풀어 다시 합치는 것을 말한다.
- 다시 말해 분할 정복은 상단에서 분할하고 중앙에서 정복하며 하단에서 조합하는 형태를 가진다.
- 분할 : 문제를 더 이상 분할할 수(쪼갤 수) 없을 때까지 동일한 유형의 여러 하위문제로 나누는 것
- 정복 : 가장 작은 단위의 하위문제를 해결하여 정복하는 것(문제를 푸는 것)
- 조합 : 하위 문제에 대한 결과를 원래 문제에 대한 결과로 조합하는 것
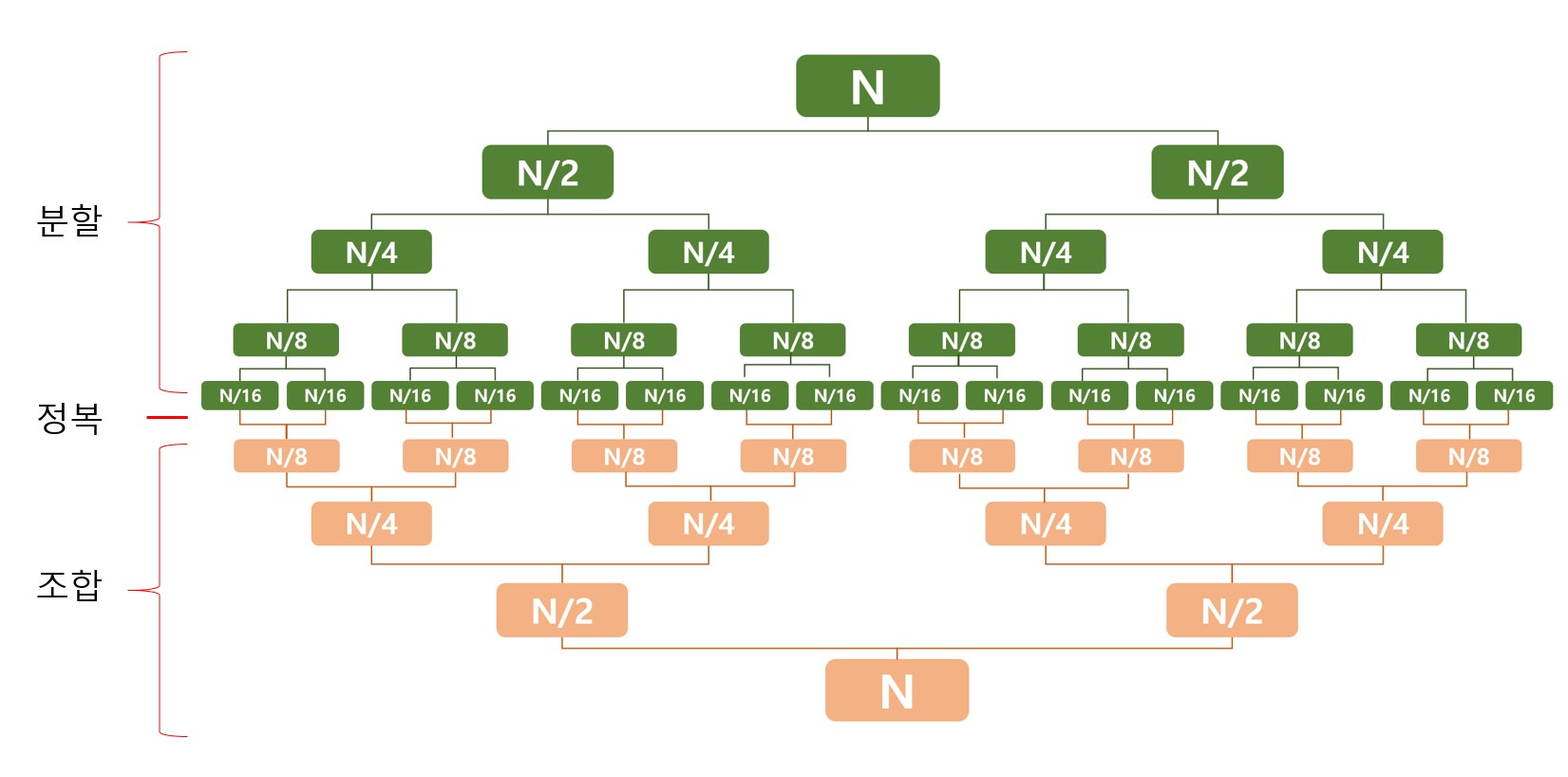
- 그림으로 설명하면 위와 같다.
적용 방식
- 재귀적으로 자신을 호출하여 그 연산의 단위를 줄여가는 방식
의사 코드
function F(x) :
if F(x)가 간단/단순 then :
return F(x)를 계산한 값;
else
x를 x₁과 x₂로 분할
F(x₁)과 F(x₂)를 호출
retrun F(x₁)와 F(x₂)로 구한 F(x) 값;장점
- 어려운 문제를 나누어 해결함으로써 풀 수 있게 된다.
- 특징상 병렬적으로 문제를 해결하는데 큰 장점을 가지고 있다.
단점
- 재귀적인 함수 호출로 인한 오버헤드가 발생할 수 있다.
- 스택에 다양한 데이터를 보관하고 있어야하므로(각 분할된 문제의 값들) 스택오버플로우 발생 및 과도한 메모리 사용 우려가 있다.
- 'F(x)가 간단하다.'라는 정의가 난해하다.
로직
"막연하게 글로써 설명하면 해당 알고리즘에 대해 긴가민가할 수도 있다. 그래서 코드로 정리해서 설명을 해보고자 한다."
- 코드로 분할 정복 알고리즘을 표현하자면 아래와 같다.
// 큰 문제를 작은 문제로 분할하는 코드
static void mergeSort(int left, int right){
//왼쪽 요소가 오른쪽 요소보다 같거나 큰 경우는 모두 분할한 경우이다.
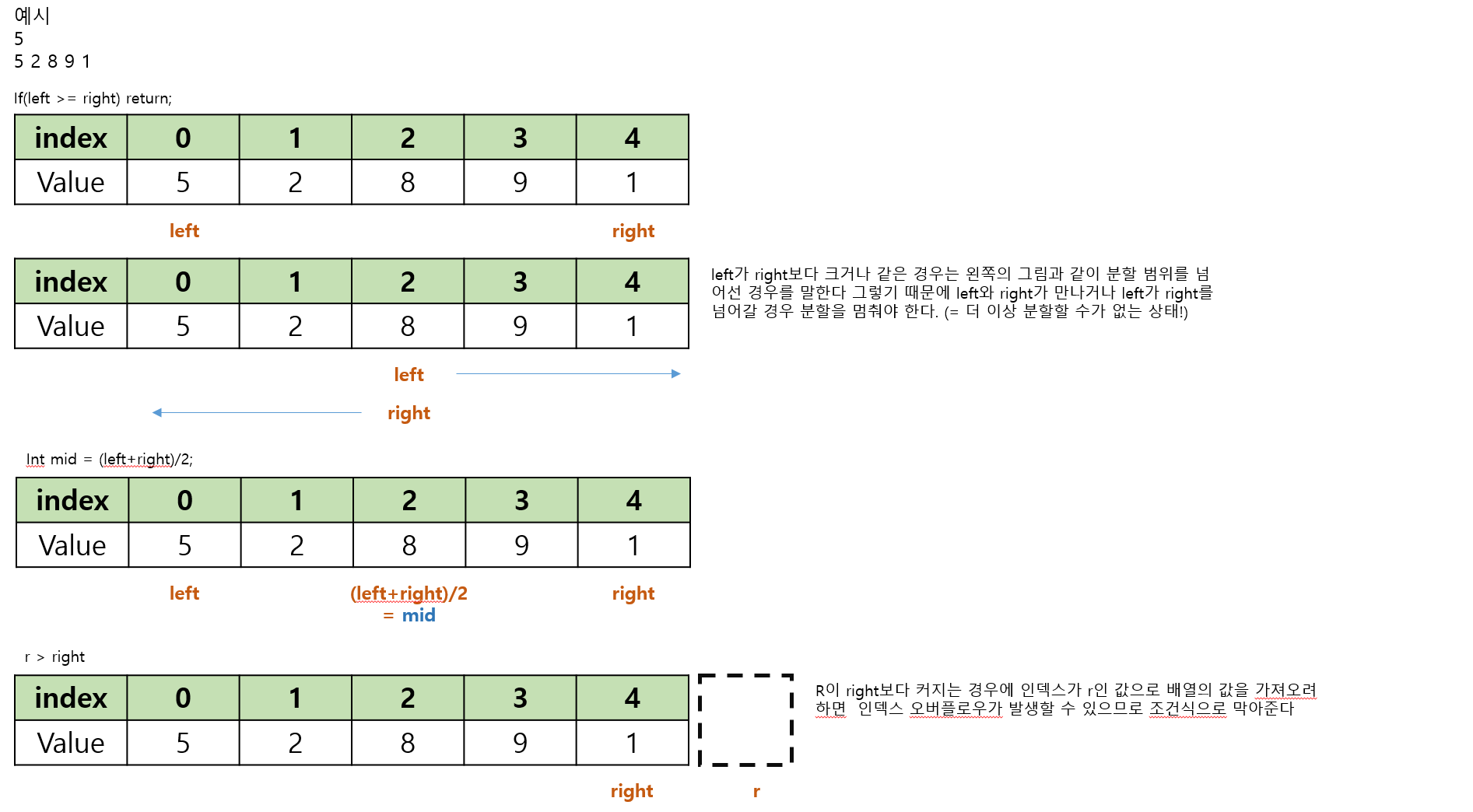
if(left >= right) return;
//주어진 왼쪽 요소와 오른쪽 요소의 중심 값을 찾기
int mid = (left+right)/2;
mergeSort(left, mid); //분할 - 왼쪽 부분
mergeSort(mid+1, right); //분할 - 오른쪽 부분
//분할 후 합치기(조합)
merge(left, mid, right);
}
//분할한 문제를 다시 합치는 코드
static void merge(int left, int mid, int right){
int l = left; // 왼쪽 요소의 시작점
int r = mid+1; // 오른쪽 요소의 시작점
int idx = l; // 정렬 시작 점
// 왼쪽 요소의 시작점이 왼쪽 요소 끝(=mid)보다 작거나 같은 경우는 아직 조회하지 못한게 있는 경우
// 오른쪽 요소의 시작점이 오른쪽 요소 끝(=right)보다 작거나 같은 경우는 아직 조회하지 못한게 있는 경우
// => 즉 왼쪽 요소나 오른쪽 요소 중 조회하지 못한게 있는 경우(정렬하지 못한게 있는 경우)
while(l <= mid || r <= right){
// 오른쪽 분할의 원소를 모두 가져온 경우(=오른쪽 요소쪽은 정렬이 완료가 된 경우/ 단, 왼쪽 요소를 고려안하고 오른쪽 요소끼리만)
// 왼쪽 분할에서 가져오지 않은 원소가 있는 경우
// 해당 원소(l)가 오른쪽 원소보다 작을 경우)
if(r > right || (l <= mid && arr[l] < arr[r]){
tmp[idx++] = arr[l++];
}else{ //그 외
tmp[idx++] = arr[r++];
}
}
}- 코드를 설명하자면 이 로직이 주 로직인데 작동하는 코드로 변경하면, 아래와 같다.
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[] arr, tmp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
arr = new int[N];
tmp = new int[N];
st = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++){
arr[i] = Integer.parseInt(st.nextToken());
}
arrayDivid(0, N-1);
for(int i = 0; i < arr.length; i++){
System.out.print(arr[i] + " ");
}
}
static void arrayDivid(int left, int right){ //분할
if(left >= right) return; //더 이상 정렬할 요소가 없을 경우
int mid = (left+right)/2; //중간 값
arrayDivid(left, mid); //왼쪽 분할
arrayDivid(mid+1, right); //오른쪽 분할
arraySort(left, mid, right);
}
static void arraySort(int left, int mid, int right){ //정렬 후 조합
int l = left; //왼쪽 시작점
int r = mid+1; //오른쪽 시작점
int sortStart = l; //정렬 시작점
while(l <= mid || r <= right){ //정렬할게 남아 있을 경우
//오른쪽 정렬이 끝난 경우
// 왼쪽 정렬은 아직 마치지 않았고 왼쪽 정렬이 오른쪽 정렬보다 작은 경우
//=> 왼쪽에서 가져온다.
if(r > right || (l <= mid && arr[l] < arr[r])){
tmp[sortStart++] = arr[l++];
}else{ //그 외의 경우에는 오른쪽에서 가져온다
tmp[sortStart++]= arr[r++];
}
}
for(int i = left; i <= right; i++){
arr[i] = tmp[i];
}
}
}- 아직 코드 주석으로는 약간 설명이 미흡할 수 있기 때문에 설명이 부족한 부분을 그림으로 설명하면 아래와 같다.