백트래킹(BackTracking)이란?
해를 찾는 도중 해가 절대 될 수 없다고 판단되면, 되돌아가서 해를 다시 찾아가는 기법을 말한다. (되추적)
DFS와 백트래킹(BackTracking)
DFS(Depth-First Search)
- 깊이 우선 탐색으로 가능한 모든 경로를 탐색한다. (그래프에서 깊은 부분을 우선적으로 탐색)
- 모든 경로를 탐색하는 특징으로 불필요할 것 같은 경로를 사전에 차단하지 않기 때문에 경우의 수를 줄이진 못한다.
백트래킹(BackTraking)
-
알고리즘 기법 중 하나로 재귀적으로 문제를 해결하되 현재 재귀를 통해 확인 중인 상태가 제한 조건에 위배가 되는지 판단하고, 해당 상태가 위배되는 경우 해당 상태를 제외하고 다음 단계로 넘어간다.
-
말이 어렵지만, 위에서 말한 대로 해를 찾는 도중 해가 절대 될 수 없다고 판단되면, 되돌아가서 다시 해를 찾는다고 생각하면 된다.
-
여기서 KEY POINT는 더 이상 탐색할 필요가 없는 상태를 제외한다는 것인데, 이를 가지치기라고 한다.
여기까지만 읽었다면... DFS와 백트래킹은 무슨 관계가 있는걸까? 라고 의문을 가질 수 있다.
-
백트래킹은 모든 경우의 수에서 조건을 만족하는 경우를 탐색하는 것이기 때문에 완전탐색기법인 DFS(깊이우선탐색), BFS(너비우선탐색)로 모두 구현이 가능하다.
-
백트래킹 특성에서 조건에 부합하지 않으면 이전 수행으로 돌아가야 함으로 BFS보다는 DFS이 구현하기 더 편하기 때문에 주로 DFS를 사용한다. (이에 대한 설명은 아래의 사진을 보면 이해할 수 있을 것이다.)
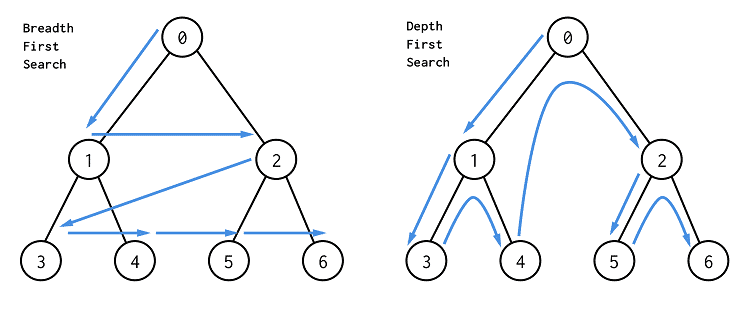
이미지 출처 : https://velog.io/@vagabondms/DFS-vs-BFS
백트래킹(BackTraking) 예시
구현 예시 3X3 행렬 선택 게임
- 규칙 : 아래와 같은 행렬이 존재할 때 3개의 숫자를 선택하는데, 단 선택한 숫자들의 행과 열은 모두 중복되면 안된다.(즉 뽑아내는 숫자의 행과 열이 모두 달라야한다)

- 위의 행렬을 3X3행렬 선택 게임의 규칙을 적용한 트리 구조로 바꾸면 아래와 같다.
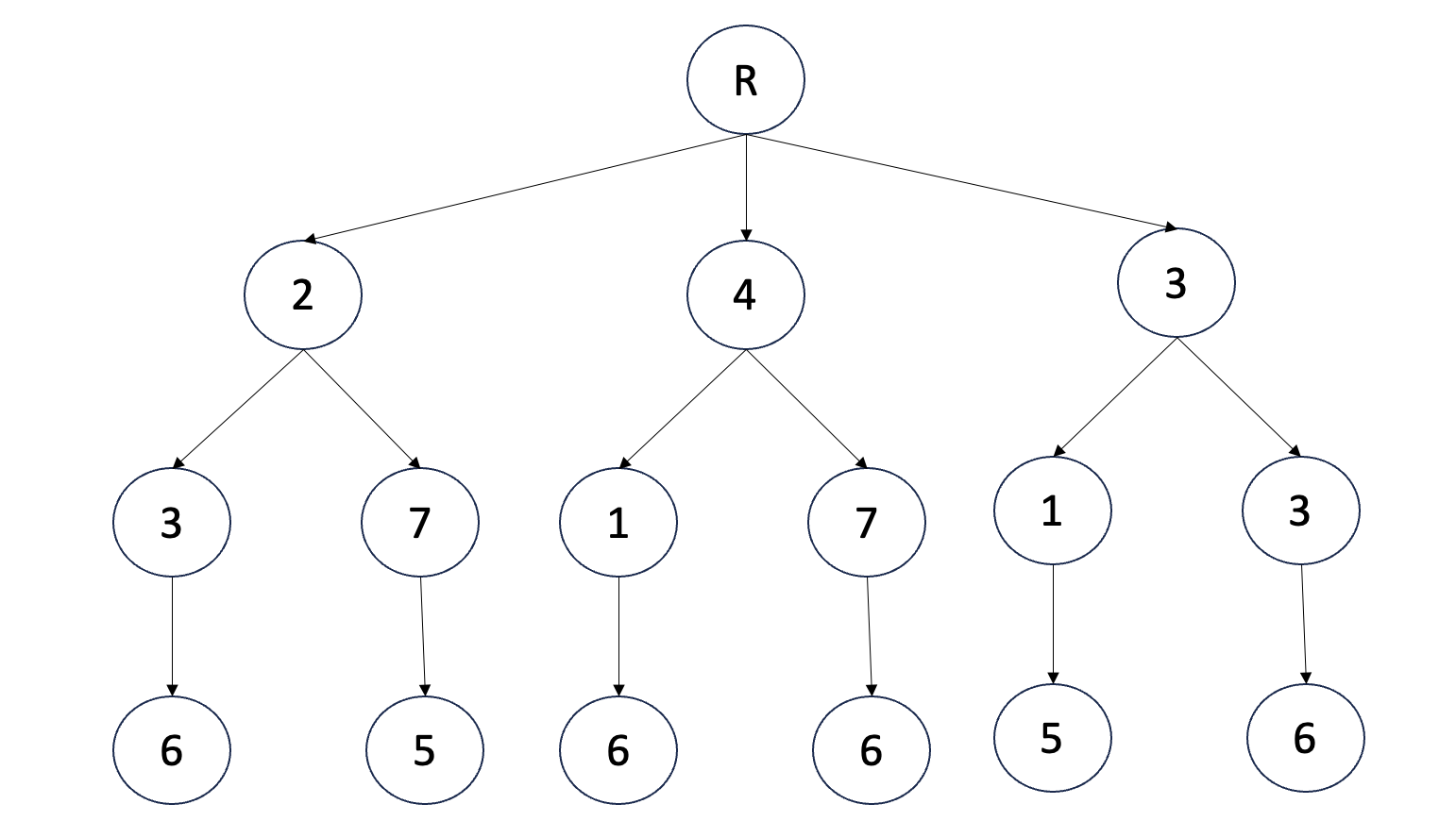
- 같은 행과 같은 열에 있는 것을 제외하기 때문에 이러한 트리가 나온다. 예시로 (0,0)에 있는 2라는 값을 처음 선택했다면, 바로 그 아래 행은 (1,1), (1,2)밖에 오지 못한다. 그 이유는 앞에서 계속 얘기했다시피 같은 행과 열은 포함하지 않기 때문이다!
- 백트래킹은 이러한 방식으로 조건을 통해서 탐색할 상태가 조건에 위배되지 않는지 판별하고, 위배되지 않는 상태만을 추가하여 탐색하는 기법이라고 볼 수 있다.
코드로써 구현
# import java.io.*;
public class Main {
static int[][] list;
static boolean[] check;
public static void main(String[] args) throws IOException {
list = new int[][]{{2, 4, 3}, {1, 3, 7}, {6, 5, 6}}; //3X3 행렬
check = new boolean[]{false, false, false}; //조건 판별 체크
backTracking(0,0);
}
static void backTracking(int row, int score) {
if (row == 3) { //재귀함수 마치는 조건
System.out.println(score);
return;
}
for (int i = 0; i < 3; i++) {
if (check[i] == false) {
check[i] = true;
backTracking(row+1, score + list[row][i]); //자식노드 방문
check[i] = false; //자식노드 방문했으면 부모노드 다시 방문기록지움
}
}
}
}실행 결과값

- 각 재귀를 했을 때의 점수 값들이다. (경우의 수 6가지의 점수가 모두 나온 것을 확인할 수 있다.)
