"시작하기 전에"
백준 동적 프로그래밍 문제를 어느 정도 푼 후에 정리를 하게 되어 순서가 뒤죽박죽 된 느낌이지만...
이대로 쭉 진행하면 이론을 완벽히 이해해서 문제를 푸는 느낌이 아니라 문제를 풀기 위해 공식을 넣는 느낌이라 풀면서도 '맞나...? 문제풀이를 더 진행하기엔 무리이지 않을까' 라는 생각이 계속 들었다.. 급하게 개념 정리를 하고 넘어가기로!!
동적 프로그래밍(Dynamic Programming ; DP)
동적 계획법(=DP)이란?
- 특정 범위까지의 최적의 해(상위 문제)를 구하기 위하여 다른 범위까지의 최적의 해(하위 문제)를 이용하여 효율적으로 최적의 해를 구하는 알고리즘 설계 기법이다.
- 쉽게 말해, 하나의 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것을 의미한다.
- 알고리즘 설계 기법(패러다임) 중 하나에 속한다.
DP는 왜 사용하는가?
- 여태까지 백준 문제를 풀면서 DP를 적용한 코드를 보면 재귀와 비슷한 것을 볼 수 있다. (아래와 같이)
/* DP를 적용한 코드 예시*/
static int yesDPSoultion(int N){ //DP 사용하는 피보나치 솔루션
if(yesDP[N] == null) {
yesDP[N] = (yesDPSoultion(N - 1) + yesDPSoultion(N - 2));
}
return yesDP[N];
}
-
위와 같이 getFibonacci(num)라는 함수를 재귀하는 것을 볼 수 있다.
-
코드를 보면 피보나치 구하는 문제라는 것은 익히 알 것이다! 다만! 다른 점이라면 바로 조건식! DP의 핵심인 부분이다!
-
예를 들어 그냥 DP를 적용하지 않고 피보나치를 구한다고 치자. (아래의 코드로 볼 수 있다.)
/* DP를 적용하지 않은 예시*/
static int noDPSoultion(int N) { //DP 사용하지 않은 피보나치 솔루션
if(N <= 1){
return N;
}
return (noDPSoultion(N-1) + noDPSoultion(N-2));
}-
조건식을 따로 주지 않았으니 이전의 계산한 값도 무조건 계산을 할 것이다. 코드 상으로 봤을 때 "크게 차이가 있을까 싶지만 구하려는 숫자가 클 수록 기하급수적으로 효율성의 차이가 생길 것이다.
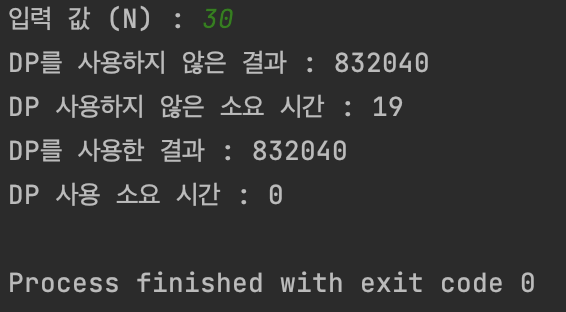
-
N이 30일 경우 소요 시간이 DP를 사용할때와 아닐떄의 차이가 큰 것을 알 수 있다.
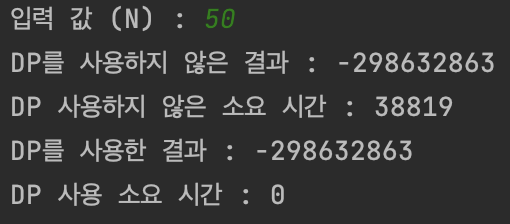
-
입력 값이 커질 수록 소요시간은 더 기하급수적으로 올라가는 것을 알 수 있다. (DP를 사용하지 않으면 계산해야하는 부분이 훨씬 많아지는 거니까...)

-
즉, 위의 그래프와 같이 같은 색의 부분을 한번만 계산하면 DP를 적용한 것이고, 그렇지 않고 그때 그때 다시 구하면 DP를 사용하지 않는 코드라 볼 수 있다.
이러한 이유로 DP를 사용한다. (좀 더 효율 적인 코딩을 위해?)
DP의 조건
- 겹치는 문제의 존재
- 이 조건은 분할 정복이냐 동적계획법인지 나누게 되는 중요한 조건에 속한다.
- 동적계획법 : 앞에서 설명했듯이 작은 부분문제들이 반복되는 것(답이 바뀌지 않음)을 이용해 풀어나가는 방법
- 분할정복 : 큰 문제를 해결하기에 어려움이 있어 그냥 작은 문제로 나누어 푸는 방법이기 때문에 작은 문제에서 반복이 일어나는 부분이 없다.
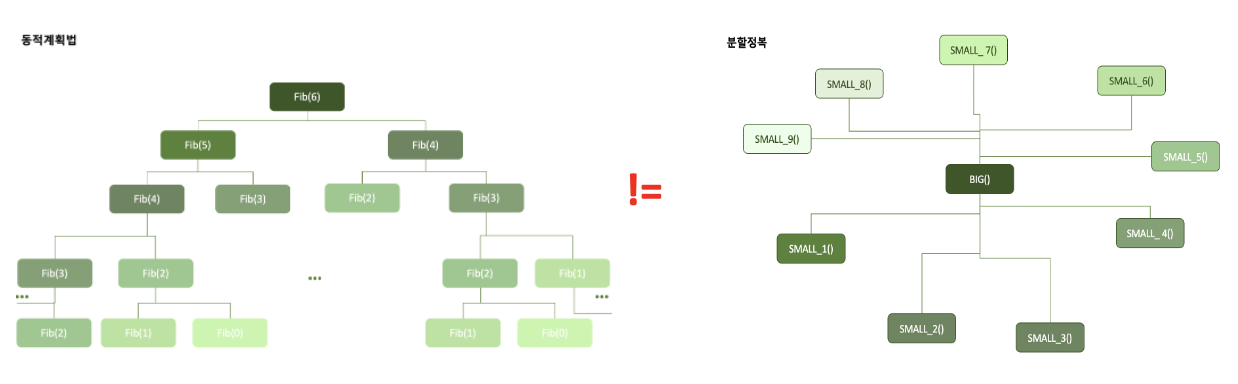
- 최적의 결과
- 부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있어야 한다.
- 쉽게 말해 최적해 + 최적해 = 최적해이어야 한다는 의미!
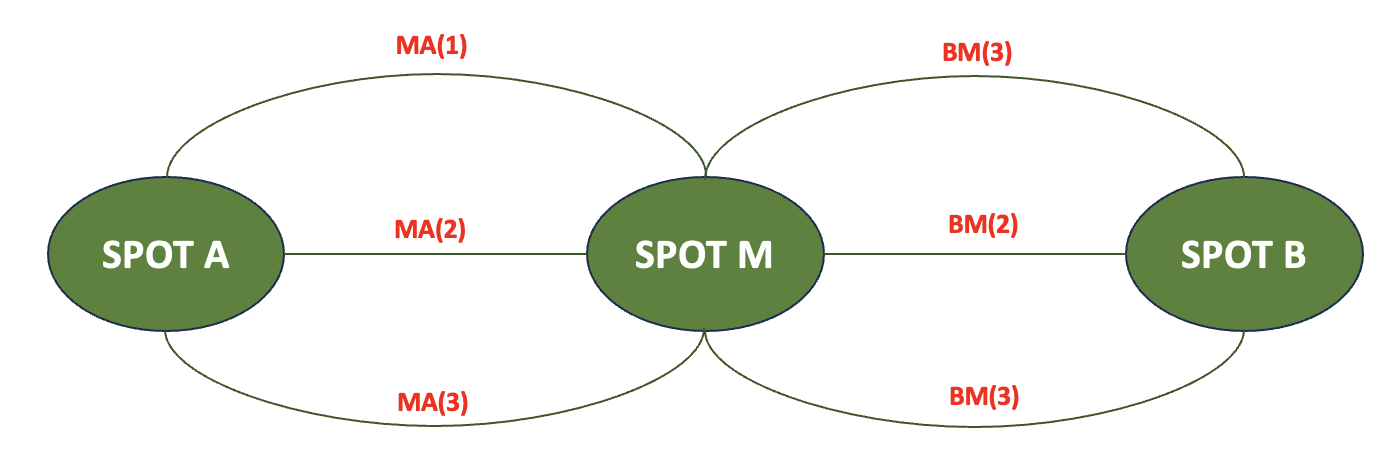
- A -> B로 가는데 최적의 거리를 구할 때
- 만약, A -> M 최적이 MA(2)이고, M -> B 최적이 BM(2)일 때
- A –> B의 최적은 무조건 MA(2) + BM(2)밖에 올 수 없다.
DP의 구현 방식
- Bottom-Up 방식
- 방식명 그대로 아래(Bottom)에서 부터 계산을 수행 하고 누적으로 위의 전체 문제(UP)를 해결하는 방식을 의미한다.
- 코드를 예시로 들면 아래와 같다.
/*
import문 생략
*/
static Integer[] DP;
public static void main(String[] args) throws IOException {
int N = 45;
DP = new Integer[N+1];
//초기 값
DP[0] = 0;
DP[1] = 1;
}
// Bottom-Up방식으로 피보나치 수 구하는 경우
public static int bottom_Up(int n){
// 반복문을 사용 (아래(2) -> 위(N) 까지)
for(int i=2; i<=n; i++){
// Table을 채워나감! -> 채워가는 방식이 table-filling이라 하며, 그렇기 때문에 Memoization이 아닌 Tabulation이라고 부른다.
DP[i] = DP[i-1] + DP[i-2];
}
return DP[n];
}- Top-Down 방식
- 위(UP = dp[n])의 값을 찾기 위해 해당 값을 바로 호출을 시작하여 아래(DOWN = dp[0])의 상태까지 내려간 다음 해당 결과 값을 재귀를 통해 전이시켜 재활용하는 방식을 의미한다.
- 코드를 예시로 들면 아래와 같다.
/*
import문 생략
*/
static Integer[] DP;
public static void main(String[] args) throws IOException {
int N = 45;
DP = new Integer[N+1];
//초기 값
DP[0] = 0;
DP[1] = 1;
}
// Top-Down 방식으로 피보나치 수 구하는 경우
public static int top_Down(int n){
// 이미 계산한 값이면 -> 이미 계산값을 메모하여 재사용하므로 Memoization이라 부른다.
if(DP[n] != null) return DP[n];
// 재귀를 사용
DP[n] = topDown(n-1) + topDown(n-2);
return DP[n];
}
- 주로 나는 TOP-DOWN이 편해서 TOP-DOWN만 썼지만, 개념을 정리한 만큼 적절하게 사용할 수 있도록...😭🙆🏻♀️

