문제 링크
https://www.acmicpc.net/problem/1463
문제 유형
DP (다이나믹 프로그래밍)
🌈문제
정수 X에 사용할 수 있는 연산은 다음과 같이 세 가지 이다.
X가 3으로 나누어 떨어지면, 3으로 나눈다.
X가 2로 나누어 떨어지면, 2로 나눈다.
1을 뺀다.
정수 N이 주어졌을 때, 위와 같은 연산 세 개를 적절히 사용해서 1을 만들려고 한다. 연산을 사용하는 횟수의 최솟값을 출력하시오.
입력
첫째 줄에 1보다 크거나 같고, 106보다 작거나 같은 정수 N이 주어진다.
출력
첫째 줄에 연산을 하는 횟수의 최솟값을 출력한다.
1. 아이디어
다이나믹 프로그래밍을 수행할 때 기억해야 하는 두가지가 존재한다.
- 이전의 값을 기억하고 그것을 지속하여 사용한다.
- 내가 계산한 값을 최적화에 직접적으로 사용할 수 있어야 한다(영향을 끼치는 값이 된다)
이 두가지 사실을 고려하면서 다이나믹 프로그래밍에 내가 적용할 수 있는 것이 무엇인지 생각해보면 된다. 내가 계산해야 하는 큰 값을 작은 부분적으로 나눌 수 있게 하고, 연산을 끝낸 값들을 재활용할 수 있게끔 코드를 짜야 한다.
즉, num이라는 숫자(입력 숫자)를 최소하능로 계산할 수 있는 연산의 횟수를 배열에 주장해두고 가장 작은 것을 나올 수 있게 해야 한다.
내가 연산에 대해서 트리로 그린 모양은 다음과 같다.
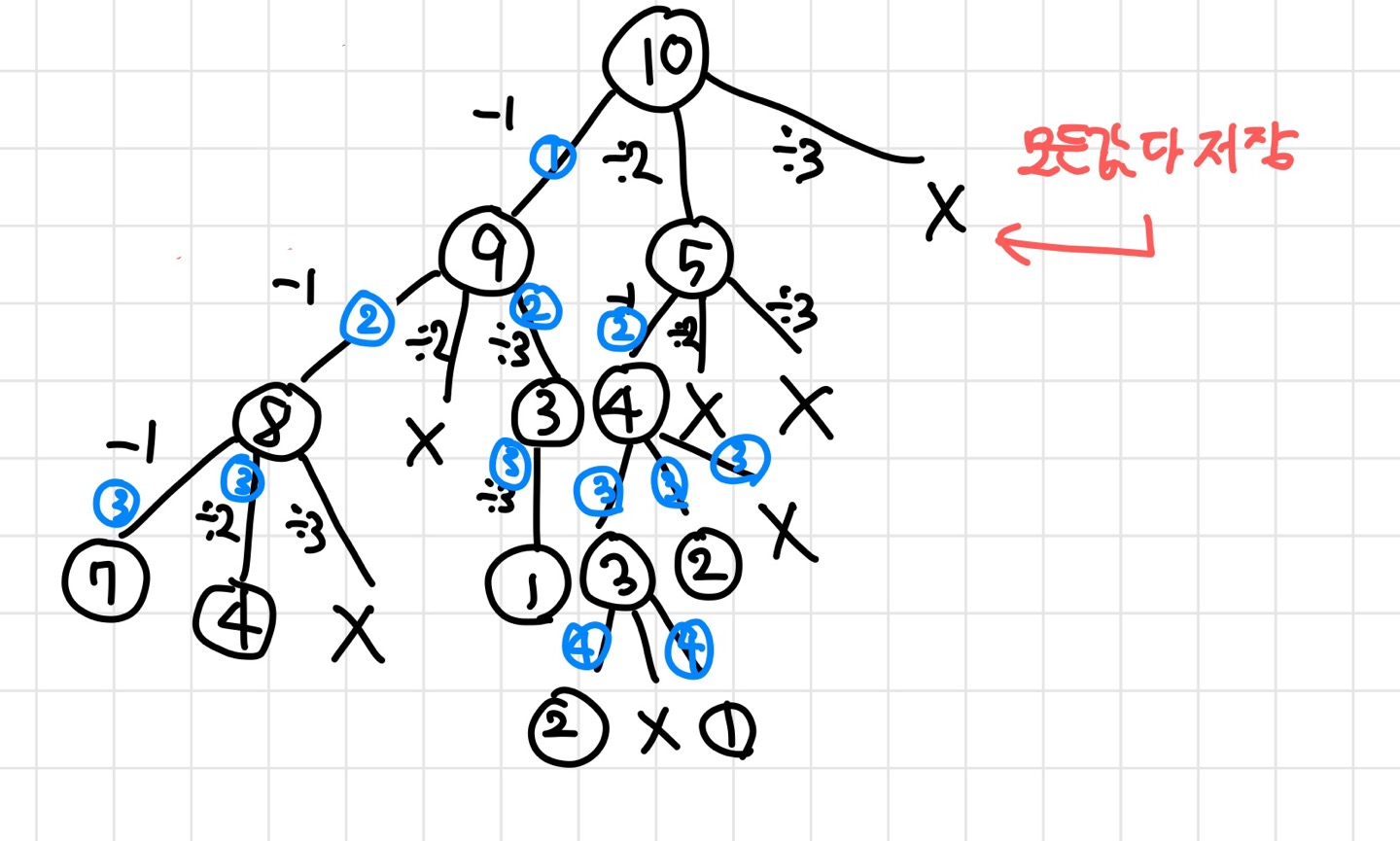
2. 풀이 방법
- 배열 d에 num을 1로 만드는 최소 연산 횟수를 저장한다.
- d[5]의 값은 5를 1로 만드는 데 걸리는 최소 연산의 횟수이다.
즉 num이 1일 때부터 우리가 입력한 수가 될 때까지의 최소 연산의 횟수를 구하면 되는 것이다.
num = 1일때는 이미 1이므로 연산이 필요하지 않다. 그래서 d[1] = 0이다. 그래서 for문은 2로 시작한다.
이제 규칙을 모르겠으면 하나하나씩 해보면서 규칙을 발견하는 것도 풀이 방법 중에 하나이다.
num = 2
2로 바로 나누어 떨어지므로 d[2] = 1
num = 3
3으로 바로 나누어 떨어지므로 d[3] = 1
num = 4
2로 나누어 떨어지므로, 4/2를 진행하고, num은 2가 된다. 2로 나누면 되니까 d[4] = 2
num = 5
5는 2,3으로 나누어 떨어지지 않는다. -1을 먼저 하고, 이후 4, 2 총 3번의 연산이 필요하여 d[5] = 3
num = 6
이 친구는 선택지가 많아 보인다.
1) 먼저 3으로 나눌 경우
6 / 3 => 2 / 2 => 1 : 2번의 연산
6 / 2 => 3 / 3 => 1 : 2번의 연산
d[6] = 2
num = 7
먼저, 7은 2,3으로 나누어 떨어지지 않으므로 1을 뺀다. 그럼 6이 된다. 우리가 위에서 이용하였던 6을 계산하는 방법을 이용하면 쉽고 빠르게 계산 가능하다.
d[7] = 3
위의 문제들을 다시 되짚어 보자. 우리가 더 큰 수를 계산하면 할 수록 예전에 계산 후 저장한 값을 이용하여 연산을 진행할 수 있음을 알 수 있다.
몇 가지 예시를 들어보자.
- 7 : d[7] = d[6] + 1
- 6은 num을 2로 나누는 연산 횟수 1번과, d[3]을 이용하거나, num을 3으로 나누는 연산 횟수 1번과 d[2]를 이용한다. 즉,
d[6] = 1 + d[6//2] or d[6] = 1 + d[6//3]
이렇게 두 가지 경우가 발생할 때에는 더 작은 값을 비교하여 d[6]에 넣어주면 된다.
이 문제를 통하여 다이나믹 프로그래밍의 원리에 대해서 더욱 잘 이해할 수 있는 대표적인 문제라고 생각한다.
3. 코드
n = int(input())
d = [0] * 1000000
for i in range(2, n+1):
d[i] = d[i-1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i//2] + 1)
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)
print(d[n])